有条件的建议去油管上看,讲的很清楚
https://www.youtube.com/watch?v=3roPs1Bvg1Q
引例:如果你是夏令营负责人,你的任务是将一群人分为两组。为了公平起见,每个人在卡片上写下了自己希望匹配的人,根据这些卡片,你要尽可能让希望彼此在一起的人更多。
1 基本概念
开花算法用于图中最大匹配的计算,为了方便理解我们给出几个概念:
1.1 匹配
若G=(V,E)是无向图,边集M属于E,M中任意两边均不相邻,M是G的匹配。下图黄色部分就是一个匹配。
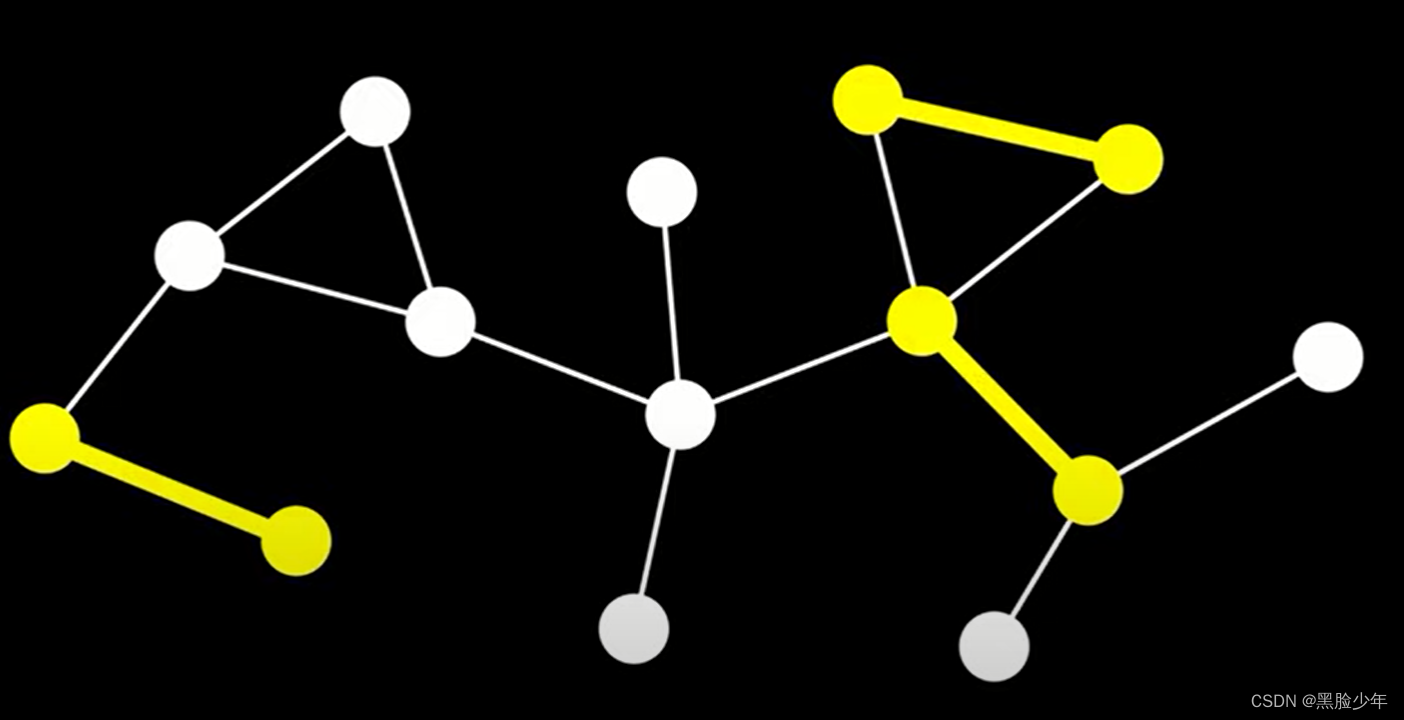
1.2 渗透点
顶点v和M中边关联,则v为渗透点,否则为非渗透点。图中橙色即为非渗透点,也是在寻找最大路径要用到的。

1.3 交错路径
M是G的一个匹配,M的交错路径是匹配路径和非匹配路径交替构成,长度可以为1。白色路径为未匹配路径,黄色为匹配路径。
1.4 增广路径
增广路径是起点和终点都是非渗透点的交错路径。主要用于改进匹配。增广路径理论上来说应该比最短路径要短。
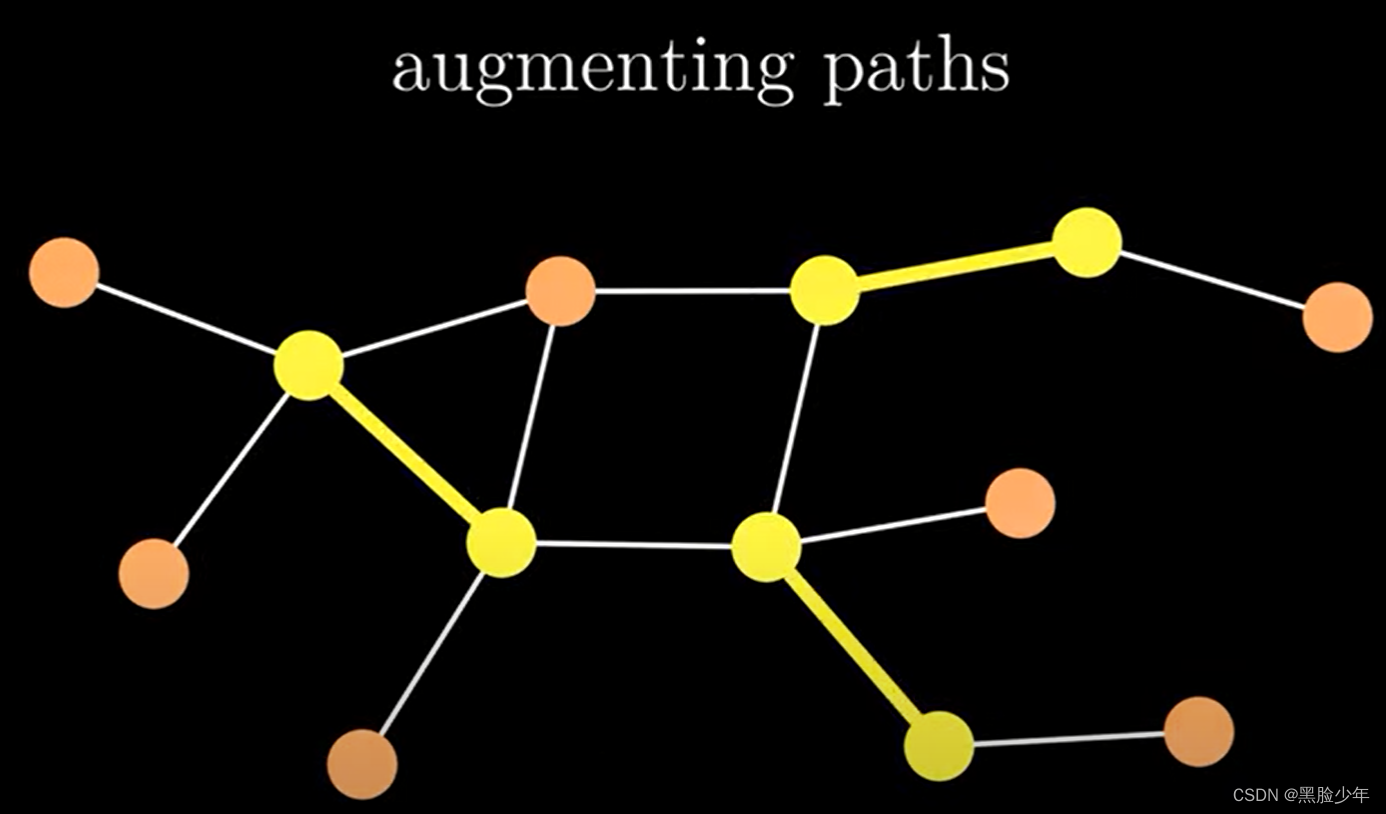
紫色部分是当前黄色匹配的增广路径。
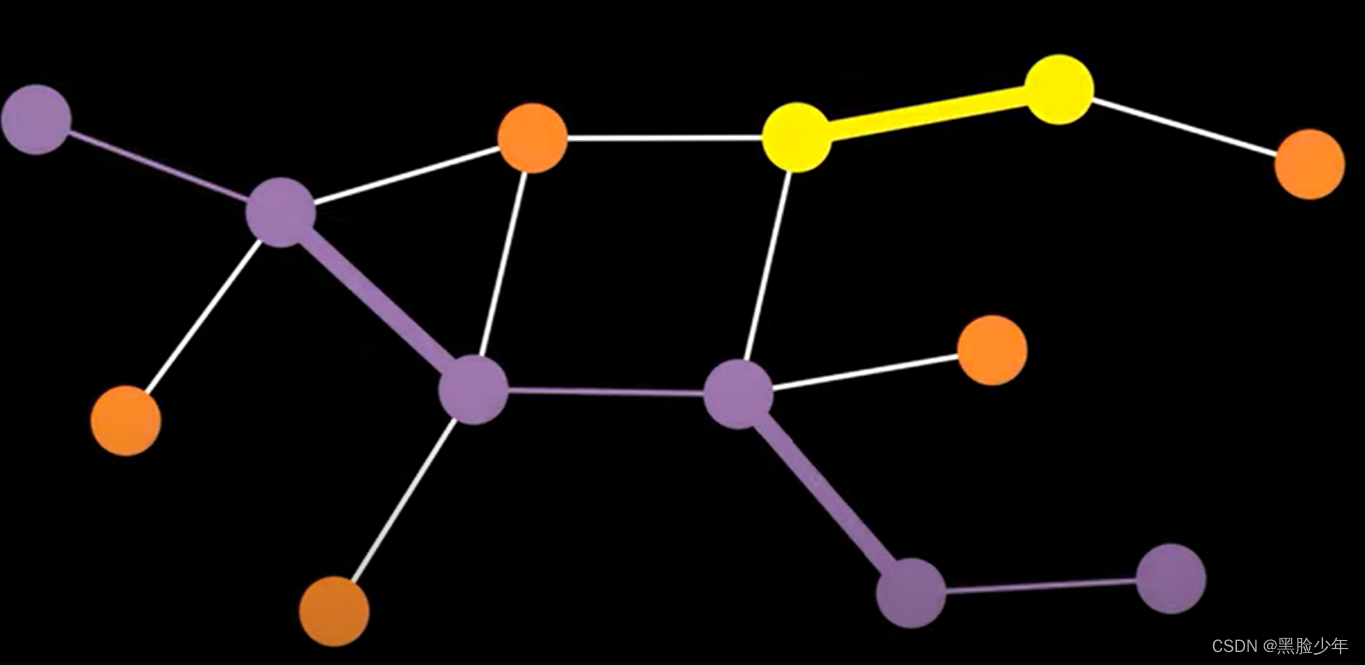
增广路径顾名思义,可以通过切换匹配和不匹配的边来增加匹配的大小。如图所示,修改非匹配边后,匹配仍然有效,但是黄色路径增加1。
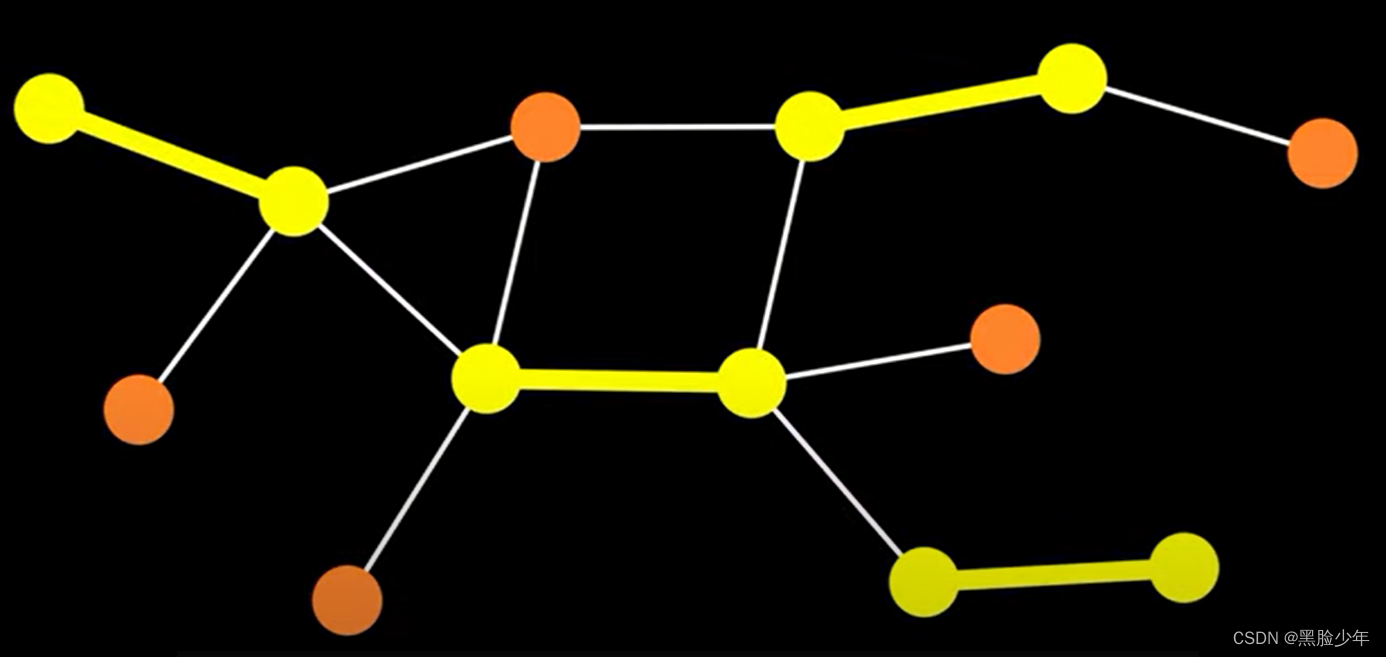
1.5 Berge定理
M是G的最大匹配的充要条件是G不包含M增长路径。可以通过增广路经反复修改,直到没有增广路径,即找到最大的匹配。
2 树
下面我们介绍如何在树上进行开花算法:
初始匹配为空,所有节点都是非渗透点。随机选取一个非渗透点,进行BFS广度优先搜索,交替添加匹配和不匹配的边。
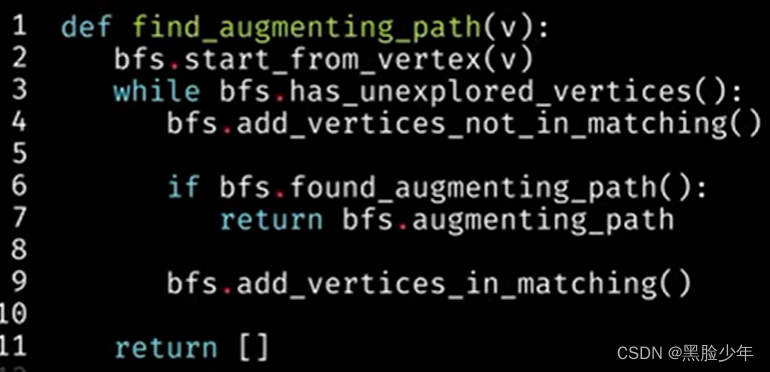
然后使用增广路径反复匹配,直到没有剩余路径即可。
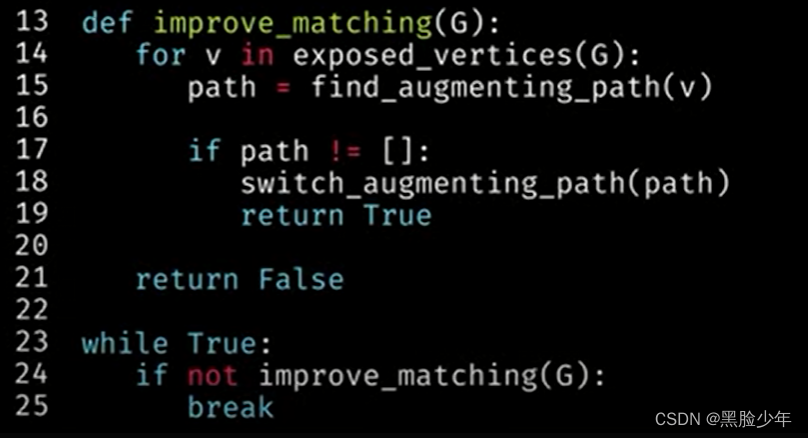
3 图
我们先看一下开花算法不适用的情况,假设我们已经找到一个匹配,希望对其进行改进达到最大匹配。
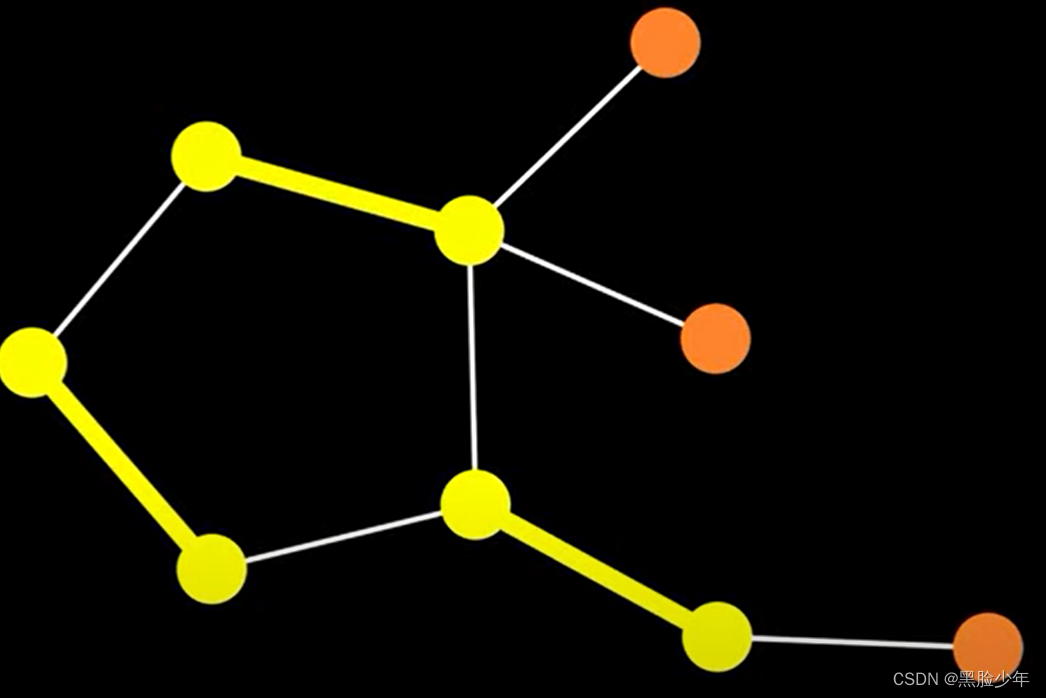
但在这张图里增广路径比最短路径要长,所以无法实现
此处,增广路径分为开花(blossom)和茎(stem)。开花和茎如下图所示,茎是一个以非渗透节点结束的交替路径。
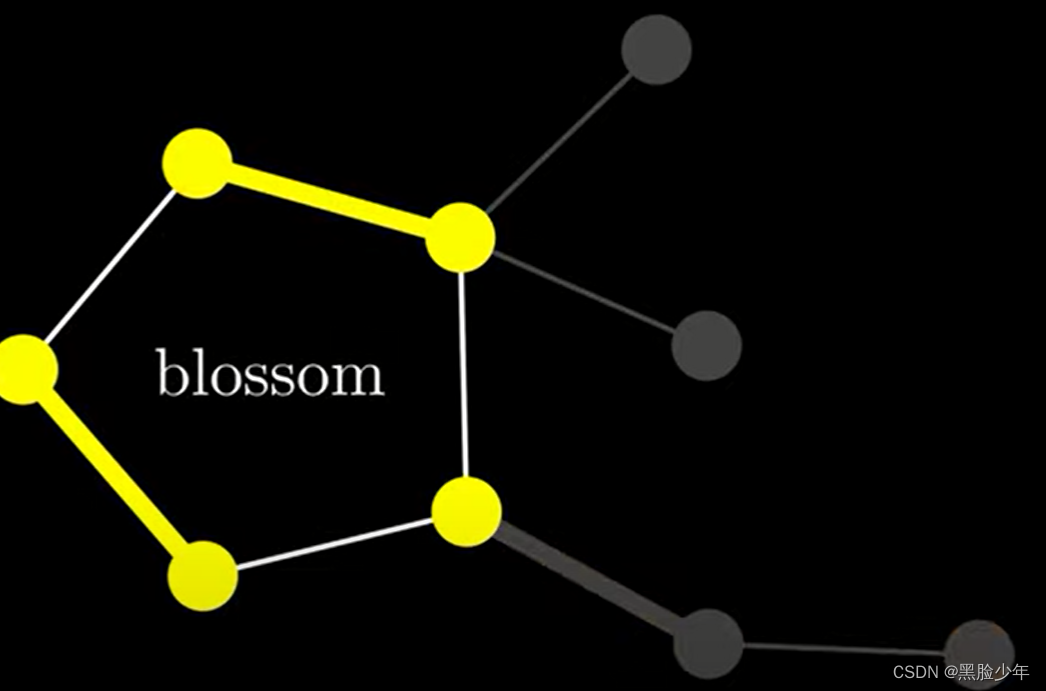
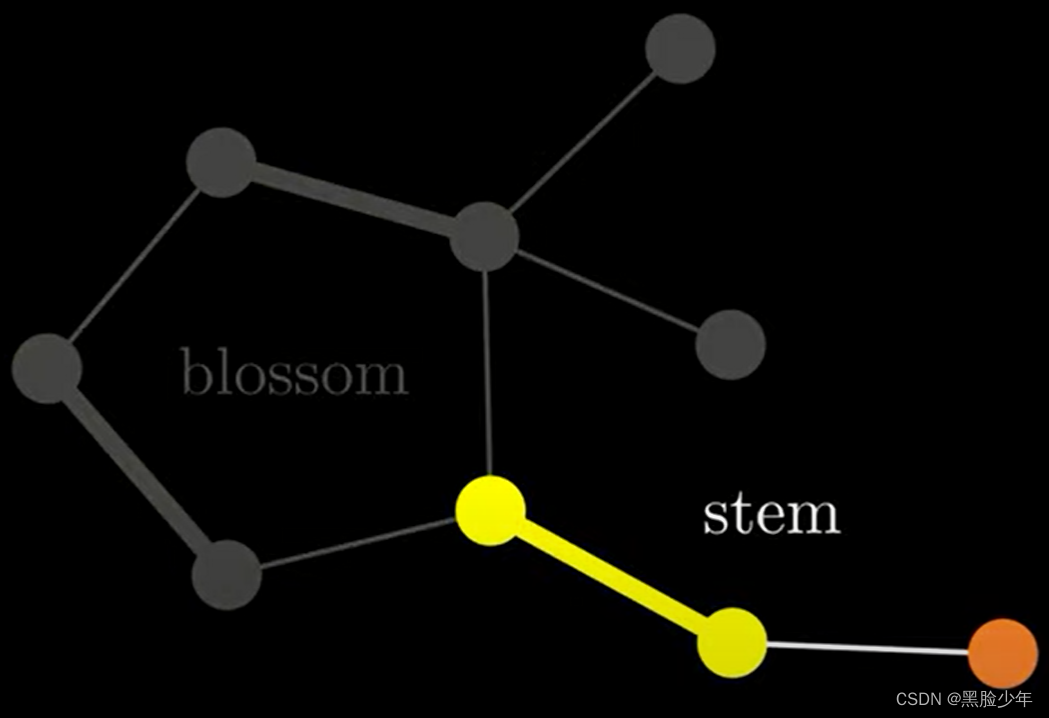
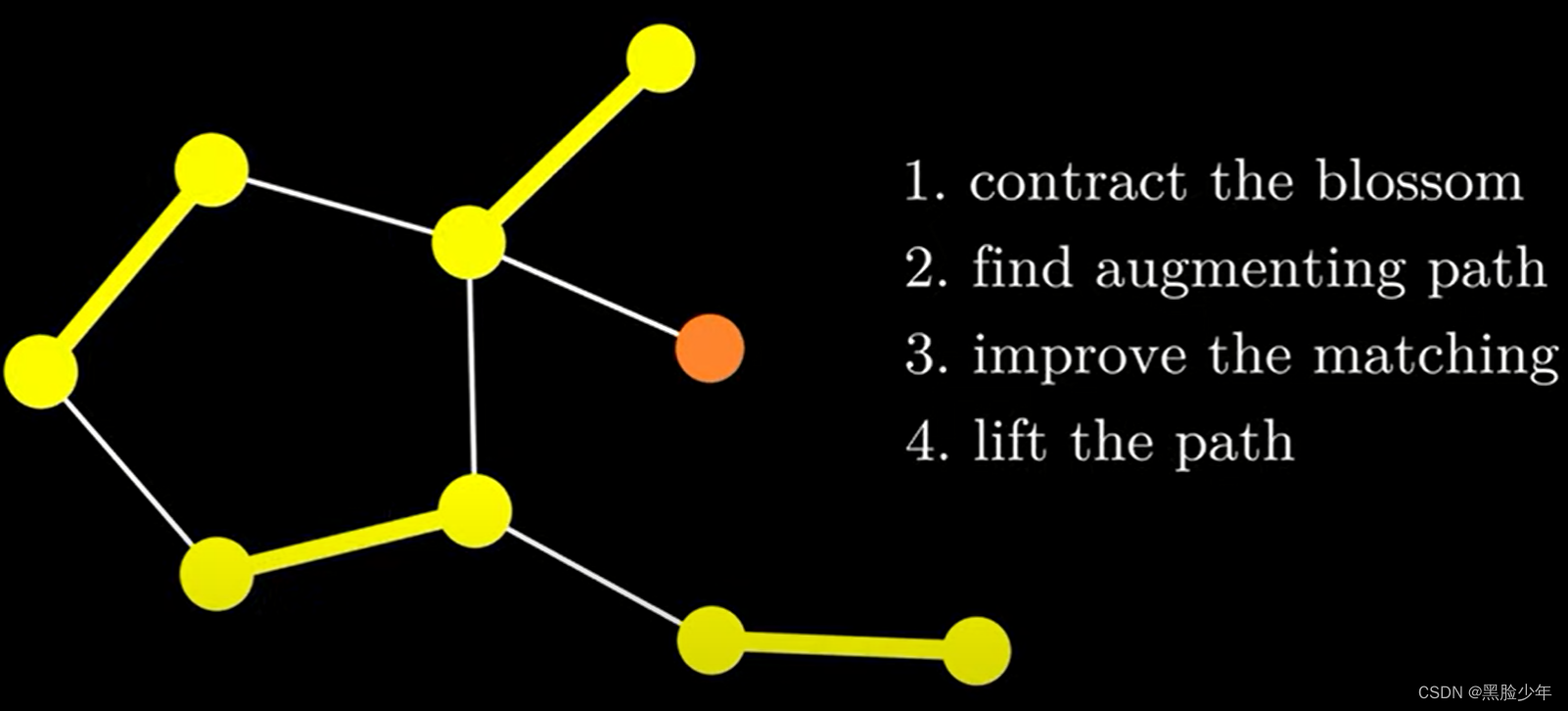
为了解决这个问题,当我们从茎进入花时,采用以下措施:
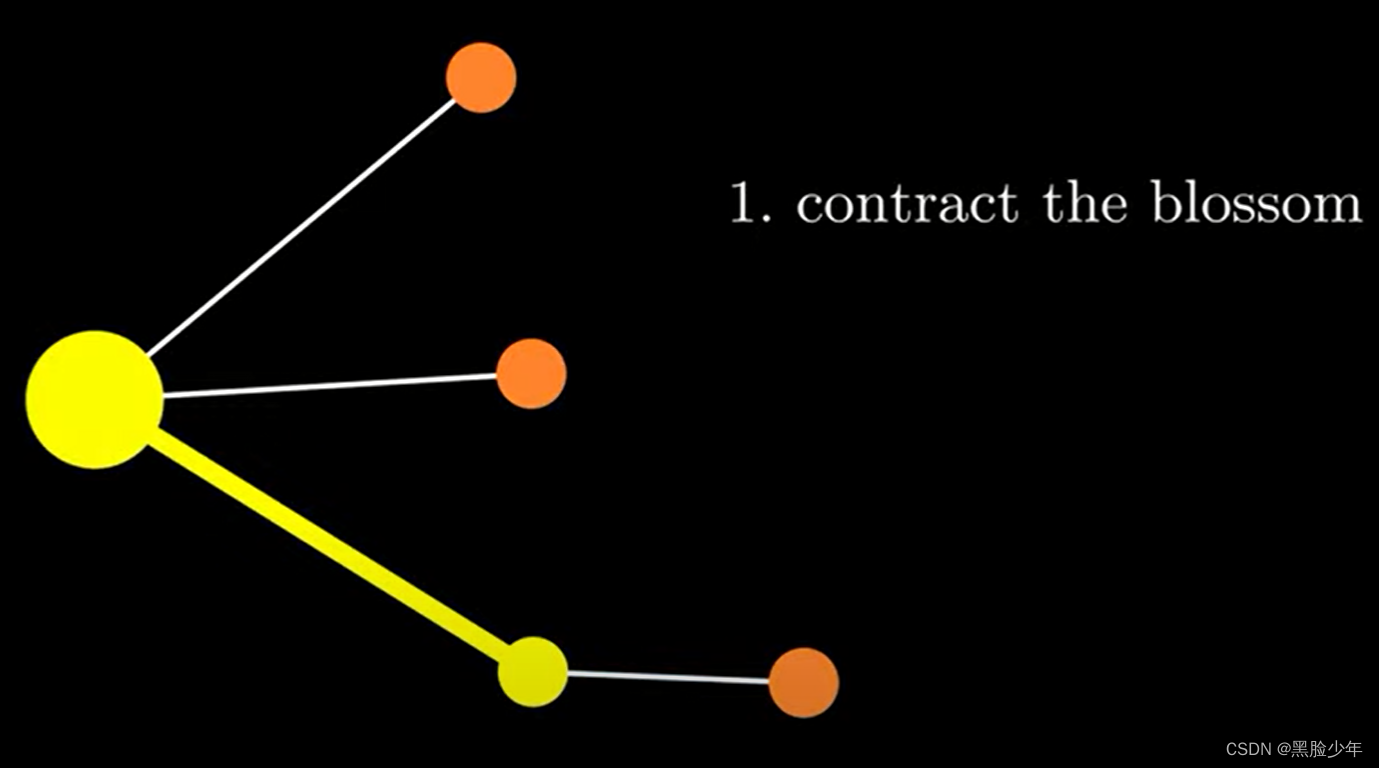
(1)把花收缩,变成渗透点
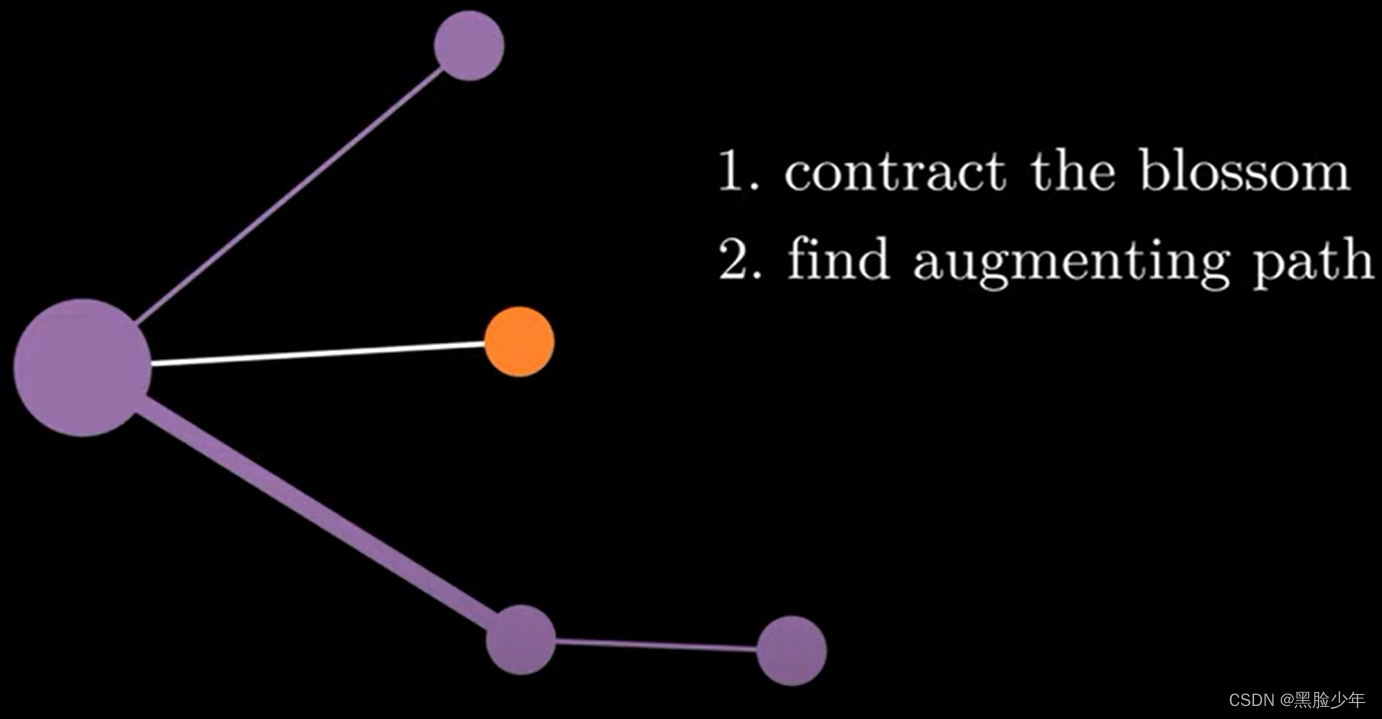
(2)在收缩图寻找增广路径
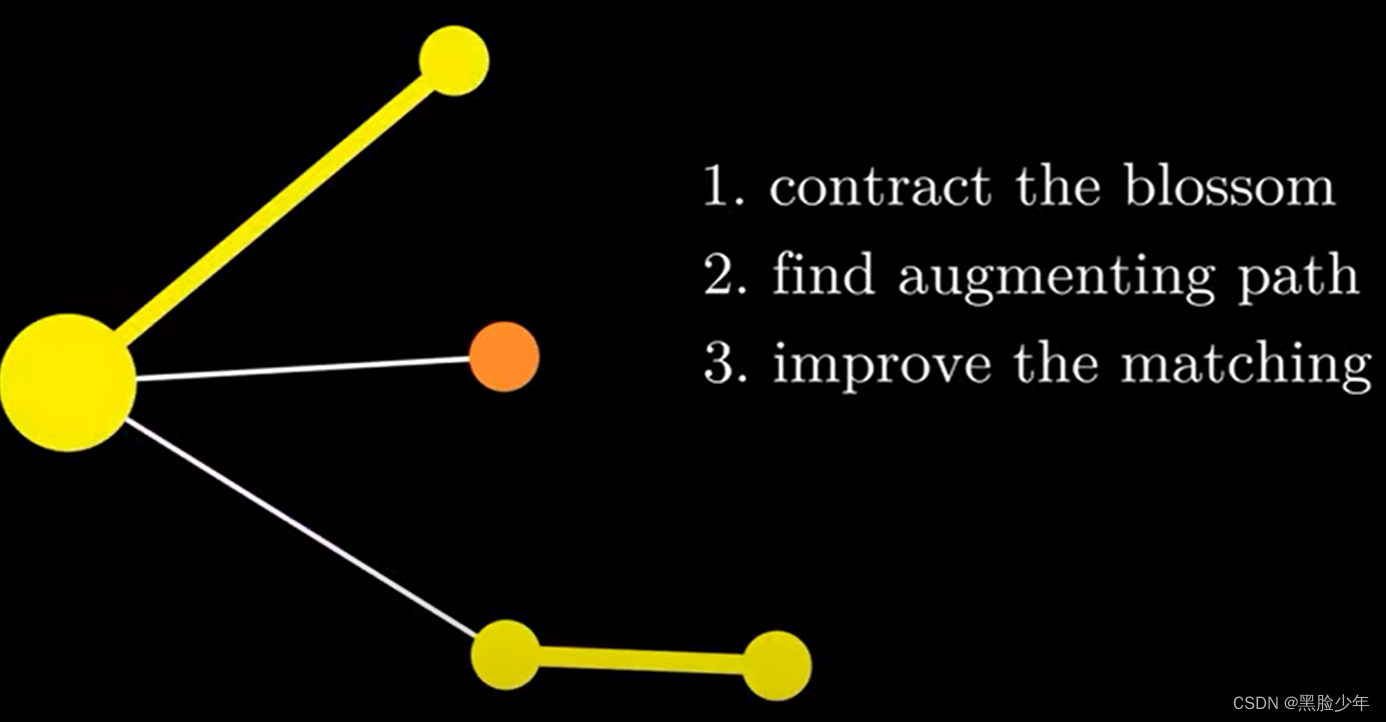
(3)增加匹配
(4)把路径变为原始图,即开花
上述步骤成立的条件是,图具有增广路径,收缩图也具有增广路径。
具体算法如下:

时间复杂度方面,朴素算法是
,开花算法是