这里写自定义目录标题
如图所示的三个曲面,小球均处于平衡点,考虑其受扰动作用,自平衡点偏离后的系统响应。
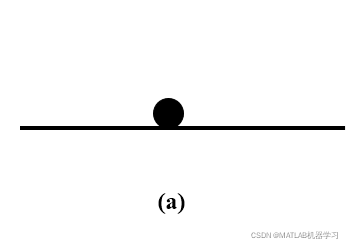
平衡点a:受扰动作用使得小球偏离原平衡点,并且使得小球达到另一个平衡点,小球的状态是自由响应且有界。
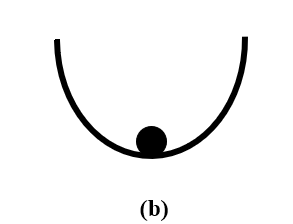
平衡点b:考虑有摩擦,小球绕原点平衡点将产生衰减振荡,小球的状态是自由响应且有界的,并且将最终返回自由平衡点。
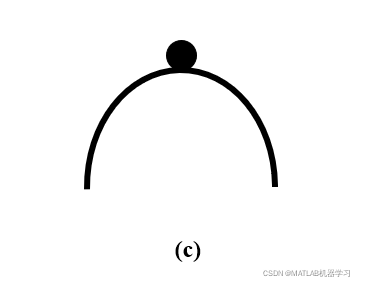
平衡点c:倘若受扰动作用使得小球偏离原平衡点,那么小球不一定能够达到下一个平衡点,那么就称小求的状态是自由响应且无界的。
1.稳定
1.1定义
设系统的初始状态
x
0
x_0
x
0
处在状态空间中,位于以平衡状态
x
e
x_e
x
e
为球心,半径为
δ
\delta
δ
的闭球域(Spherical Domain)
S
(
δ
)
S(\delta)
S
(
δ
)
内,即
∥
x
0
−
x
e
∥
≤
δ
,
t
≥
t
0
\lVert x_0-x_e \rVert \le \delta ,t\ge t_0
∥
x
0
−
x
e
∥
≤
δ
,
t
≥
t
0
若系统由初始状态
x
0
x_0
x
0
出发的系统自由响应
x
(
t
;
x(t;
x
(
t
;
x
0
x_0
x
0
,
,
,
t
0
t_0
t
0
)
)
)
在
t
→
∞
t\rightarrow\infty
t
→
∞
的过程中以平衡状态
x
e
x_e
x
e
为球心,半径为
ε
\varepsilon
ε
的闭球域
S
(
ε
)
S(\varepsilon)
S
(
ε
)
内,即
∥
x
(
t
;
x
0
,
t
0
)
−
x
e
∥
≤
ε
,
t
≥
t
0
\lVert x\left( t;x_0,t_0 \right) -x_e \rVert \le \varepsilon ,t\ge t_0
∥
x
(
t
;
x
0
,
t
0
)
−
x
e
∥
≤
ε
,
t
≥
t
0
则称该动力学系统的平衡状态
x
e
x_e
x
e
是Lyapunov意义下稳定的,或者称系统具有Lyapunov意义下的稳定。
一般地,实数
δ
\delta
δ
与
ε
\varepsilon
ε
有关,通常也和初始时刻
t
0
t_0
t
0
有关。如果
δ
\delta
δ
的大小与
t
0
t_0
t
0
无关,则称
x
x
x
是Lyapunov意义下的一致稳定(Uniformly Stable)。对于时变系统,一致稳定比稳定更具有实际意义。对于时不变系统,Lyapunov意义下的稳定与一致稳定等价。
1.2 Lyapunov稳定性定义的几何解释
以上定义意味着:在状态空间中,任意给一个以平衡状态
x
e
x_e
x
e
为中心的球域
S
(
ε
)
S(\varepsilon)
S
(
ε
)
,无论多小,总能够找到一个以原点为中心的球域
S
(
δ
)
S(\delta)
S
(
δ
)
,使得任何从
S
(
δ
)
S(\delta)
S
(
δ
)
出发的运动轨迹,都不超出
S
(
ε
)
S(\varepsilon)
S
(
ε
)
。考虑二维空间,平衡态
x
e
x_e
x
e
为坐标原点,
S
(
δ
)
S(\delta)
S
(
δ
)
和
S
(
ε
)
S(\varepsilon)
S
(
ε
)
均为一个圆。
Lyapunov意义下的稳定只能保证系统受扰运动相对于平衡状态的有界性,不能保证系统受扰运动相对于平衡状态的渐近性。Lyapunov意义下的稳定性实质上就是工程意义下的临界不稳定。
2. 渐进稳定
2.1 定义
如果平衡状态
x
e
x_e
x
e
不仅是Lyapunov稳定意义下稳定的,而且从球域
S
(
δ
)
S(\delta)
S
(
δ
)
出发的任意解
x
(
t
;
x(t;
x
(
t
;
x
0
x_0
x
0
,
,
,
t
0
t_0
t
0
)
)
)
,当
t
→
∞
t\rightarrow\infty
t
→
∞
的时,不仅不会超出球域
S
(
ε
)
S(\varepsilon)
S
(
ε
)
,而且最终收敛于平衡状态
x
e
x_e
x
e
或者其邻域,即有
lim
t
→
∞
∥
x
(
t
;
x
0
,
t
0
)
−
x
e
∥
→
0
\underset{t\rightarrow \infty}{\lim}\lVert x\left( t;x_0,t_0 \right) -x_e \rVert \rightarrow 0
t
→
∞
lim
∥
x
(
t
;
x
0
,
t
0
)
−
x
e
∥
→
0
则称平衡状态
x
e
x_e
x
e
是渐近稳定的(Asymptotically Stable)。其中球域
S
(
δ
)
S(\delta)
S
(
δ
)
被称为平衡状态
x
e
=
0
x_e=0
x
e
=
0
的吸引域,表示位于其内的所有状态点都可被吸引到平衡状态
x
e
x_e
x
e
的邻域。
同样的,如果
δ
\delta
δ
的大小与
t
0
t_0
t
0
无关,则称
x
x
x
是Lyapunov意义下的一致稳定(Uniformly Stable)。对于时变系统,一致稳定比稳定更具有实际意义。对于时不变系统,Lyapunov意义下的稳定与一致稳定等价。
2.2 几何含义
渐近稳定首先应该是Lyapunov意义下的稳定。工程上往往喜欢渐近稳定,因为希望干扰除去后,系统往往又回到原来的工作状态,这个状态正是设计系统时所期望的,也正是前面所说的平衡状态。
实际上,渐近稳定性比纯稳定性更重要。考虑到非线性系统的渐近稳定性是一个局部概念,所以简单的确定渐近稳定性并不意味着系统能够正常工作。通常有必要确定渐近稳定性的最大范围或吸引域,它是发生渐近稳定轨迹的那部分状态空间,也就是说,发生吸引域内的每一个轨迹都是渐近稳定的。
3. 大范围渐近稳定
无论是Lyapunov意义下的稳定、渐近稳定,都属于系统在平衡状态附件一小范围内的局部性质。因为系统只要在包围
x
e
x_e
x
e
的小范围内,能找到
δ
\delta
δ
和
ε
\varepsilon
ε
满足定义中的条件即可。至于从
S
(
δ
)
S(\delta)
S
(
δ
)
外出发的运动,却完全可以超出
S
(
ε
)
S(\varepsilon)
S
(
ε
)
。因此,若为了满足稳定(渐近稳定)条件,初始状态
x
0
x_0
x
0
有一定的限制,则称系统是小范围稳定(渐近稳定),也称之为局部稳定(Locally Stable)(或局部渐近稳定)。
如果系统在任意初始条件下的解
x
(
t
;
x(t;
x
(
t
;
x
0
x_0
x
0
,
,
,
t
0
t_0
t
0
)
)
)
,在
t
→
∞
t\rightarrow\infty
t
→
∞
的过程中,收敛于平衡态
x
e
x_e
x
e
或者其邻域,则平衡状态
x
e
x_e
x
e
不仅是渐近稳定的而且其范围包含整个状态空间,则称
x
e
x_e
x
e
是大范围渐近稳定或者称全局渐近稳定的平衡状态。
大范围肩颈稳定的必要条件是:状态空间中系统中只有一个平衡状态。例如某系统的状态方程为:
x
˙
=
A
x
,
∣
A
∣
≠
0
\dot{x}=Ax,\left| A \right|\ne 0
x
˙
=
A
x
,
∣
A
∣
=
0
可知零状态必然是系统的平衡状态,而若零状态渐近稳定,因为它是唯一的孤立平衡状态,则必然是大范围渐近稳定的,可见,线性系统稳定性与初始条件无关。
从实用观点出发,仅仅判知系统是小范围稳定的,系统不一定能够正常工作,一旦实际存在的干扰,使得系统的初始状态偏离而超出
S
(
δ
)
S(\delta)
S
(
δ
)
的范围,就会导致
x
x
x
有可能不反回
x
e
x_e
x
e
。因此,工程上对大范围的渐近稳定更加感兴趣。如果平衡状态不是大范围渐近稳定的,那么问题就转化为驱动渐近稳定的最大范围或吸引域,这通常非常困难。然而,对于所有的实际问题,如果能确定一个足够大的渐近稳定的吸引域,以致扰动不会超过它就可以了。对于线性定常系统,渐近稳定等价于大范围渐近稳定。但对于非线性系统,一般只考虑吸引域为有限的定范围的渐近稳定。
参考文献
1
-
现代控制理论/张莲等编著.-2版.-北京:清华大学出版社,2016
↩︎