【矩阵论】2. 矩阵分解——正规谱分解

矩阵论
1. 准备知识——复数域上矩阵,Hermite变换)
1.准备知识——复数域上的内积域正交阵
 1.准备知识——Hermite阵，二次型，矩阵合同，正定阵，幂0阵，幂等阵，矩阵的秩
 2. 矩阵分解——SVD准备知识——奇异值
 2. 矩阵分解——SVD
2. 矩阵分解——QR分解
 2. 矩阵分解——正定阵分解
 2. 矩阵分解——单阵谱分解
 2. 矩阵分解——正规分解——正规阵
 2. 矩阵分解——正规谱分解
 2. 矩阵分解——高低分解
 3. 矩阵函数——常见解析函数
 3. 矩阵函数——谱公式,幂0与泰勒计算矩阵函数
 3. 矩阵函数——矩阵函数求导
 4. 矩阵运算——观察法求矩阵特征值特征向量
 4. 矩阵运算——张量积
 4. 矩阵运算——矩阵拉直
 4.矩阵运算——广义逆——加号逆定义性质与特殊矩阵的加号逆
 4. 矩阵运算——广义逆——加号逆的计算
 4. 矩阵运算——广义逆——加号逆应用
 4. 矩阵运算——广义逆——减号逆
 5. 线性空间与线性变换——线性空间
 5. 线性空间与线性变换——生成子空间
 5. 线性空间与线性变换——线性映射与自然基分解,线性变换
 6. 正规方程与矩阵方程求解
 7. 范数理论——基本概念——向量范数与矩阵范数
 7.范数理论——基本概念——矩阵范数生成向量范数&谱范不等式
 7. 矩阵理论——算子范数
 7.范数理论——范数估计——许尔估计&谱估计
 7. 范数理论——非负/正矩阵
 8. 常用矩阵总结——秩1矩阵，优阵(单位正交阵)，Hermite阵
 8. 常用矩阵总结——镜面阵，正定阵
 8. 常用矩阵总结——单阵，正规阵，幂0阵，幂等阵，循环阵

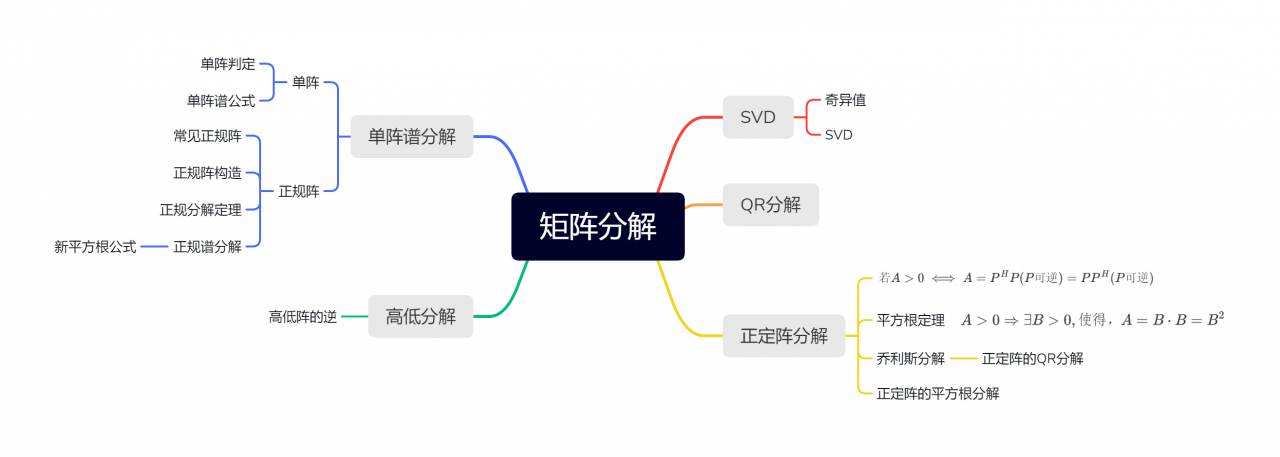
矩阵分解可以得到简化的乘积矩阵，可以简化后续的计算与处理度

在这里插入图片描述

2.4.5 正规谱分解

a. 正规分解推导

若

正规，互异根为

⋯

，则有

(

⋱

)

其中

为

阵，

−

⋯

为单位阵

(

如

(

)

(

)

(

)

可设

−

(

⋱

)

(

为

阵，

−

)

写为

(

⋱

)

(

⋱

)

⋯

(

⋱

)

则令

(

⋱

)

(

⋱

)

⋯

(

⋱

)

⇒

−

⋯

\begin{aligned} &若A=A_{n\times n} 正规，互异根为 \lambda_1,\cdots,\lambda_k，则有Q^HAQ=D=\left( \begin{matrix} \lambda_1I_1&&\\ &\ddots&\\ &&\lambda_kI_k \end{matrix} \right)\\ &其中Q为U阵，Q^H=Q^{-1},I_1,\cdots,I_k为单位阵\\ &\left(如D=\left( \begin{matrix} 2\left( \begin{matrix} 1&\\ &1 \end{matrix} \right)\\ &3\left( \begin{matrix} 1&\\ &1 \end{matrix} \right) \end{matrix} \right)=\left( \begin{matrix} 2I_1&\\ &3I_2 \end{matrix} \right)\right)\\ &可设 Q^{-1}AQ=D=\left( \begin{matrix} \lambda_1I_1&&0\\ &\ddots&\\ 0&&\lambda_kI_k \end{matrix} \right)(Q为U阵，Q^H=Q^{-1})\\ &写为D=\lambda_1\left( \begin{matrix} I_1&&0\\ &\ddots&\\ 0&&0 \end{matrix} \right)+\lambda_2\left( \begin{matrix} 0&&0\\ &I_2&\\ 0&&\ddots \end{matrix} \right)+\cdots+\lambda_k\left( \begin{matrix} 0&&0\\ &\ddots&\\ 0&&I_k \end{matrix} \right)\\ &则令D_1=\left( \begin{matrix} I_1&&0\\ &\ddots&\\ 0&&0 \end{matrix} \right),D_2=\left( \begin{matrix} 0&&0\\ &I_2&\\ 0&&\ddots \end{matrix} \right),\cdots,D_k=\left( \begin{matrix} 0&&0\\ &\ddots&\\ 0&&I_k \end{matrix} \right)\\ &\Rightarrow Q^{-1}AQ=D=\lambda_1D_1+\lambda_2D_2+\cdots+\lambda_kD_k\\ \end{aligned}

$若 A = A_{n \times n} 正规，互异根为 λ_{1}, \dots, λ_{k} ，则有 Q^{H} A Q = D = λ_{1} I_{1} ⋱ λ_{k} I_{k} 其中 Q 为 U 阵， Q^{H} = Q^{- 1}, I_{1}, \dots, I_{k} 为单位阵如 D = 2 (11) 3 (11) = (2 I_{1} 3 I_{2}) 可设 Q^{- 1} A Q = D = λ_{1} I_{1} 0 ⋱ 0 λ_{k} I_{k} (Q 为 U 阵， Q^{H} = Q^{- 1}) 写为 D = λ_{1} I_{1} 0 ⋱ 00 + λ_{2} 00 I_{2} 0 ⋱ + \dots + λ_{k} 00 ⋱ 0 I_{k} 则令 D_{1} = I_{1} 0 ⋱ 00, D_{2} = 00 I_{2} 0 ⋱, \dots, D_{k} = 00 ⋱ 0 I_{k} \Rightarrow Q^{- 1} A Q = D = λ_{1} D_{1} + λ_{2} D_{2} + \dots + λ_{k} D_{k}$

则可得出结论：

和为单位阵： $D_1+D_2+\cdots+D_k=\left( \begin{matrix} I_1&&\\ &\ddots&\\ &&I_k \end{matrix} \right)=I(单位阵) D1+D2+⋯+Dk= I1⋱Ik =I(单位阵)$
正交： $D_1D_2=0,\cdots,D_iD_j=0(i\neq j) D1D2=0,⋯,DiDj=0(i=j)$
幂等： $D_1^2=D_1,\cdots,D_k^2=D_k，且D_1^H=D_1,\cdots,D_k^H=D_k D12=D1,⋯,Dk2=Dk，且D1H=D1,⋯,DkH=Dk$

故可等价写为：

⋯

⇒

⋯

可令

⋯

⇒

⋯

\begin{aligned} &Q^HAQ=D=\lambda_1D_1+\lambda_2D_2+\cdots+\lambda_kD_k\\ &\Rightarrow A=QDQ^H=\lambda_1QD_1Q^H+\lambda_2QD_2Q^H+\cdots+\lambda_kQD_kQ^H\\ &可令G_1=QD_1Q^H,\cdots,G_k=QD_kQ^H\\ &\Rightarrow A=\lambda_1G_1+\cdots+\lambda_kG_k \end{aligned}

$Q^{H} A Q = D = λ_{1} D_{1} + λ_{2} D_{2} + \dots + λ_{k} D_{k} \Rightarrow A = Q D Q^{H} = λ_{1} Q D_{1} Q^{H} + λ_{2} Q D_{2} Q^{H} + \dots + λ_{k} Q D_{k} Q^{H} 可令 G_{1} = Q D_{1} Q^{H}, \dots, G_{k} = Q D_{k} Q^{H} \Rightarrow A = λ_{1} G_{1} + \dots + λ_{k} G_{k}$

有类似推论：

G

1

+

G

2

+

⋯

+

G

k

=

I

G_1+G_2+\cdots+G_k=I

$G_{1} + G_{2} + \dots + G_{k} = I$

∵

G

1

+

G

2

+

⋯

+

G

k

=

Q

(

D

1

Q

−

1

+

D

2

+

⋯

+

D

k

)

Q

−

1

=

Q

I

Q

−

1

=

I

\because G_1+G_2+\cdots+G_k=Q(D_1Q^{-1}+D_2+\cdots+D_k)Q^{-1}=QIQ^{-1}=I

$∵ G_{1} + G_{2} + \dots + G_{k} = Q (D_{1} Q^{- 1} + D_{2} + \dots + D_{k}) Q^{- 1} = Q I Q^{- 1} = I$
G

1

G

2

=

0

,

⋯

,

G

i

G

j

=

0

(

i

≠

j

)

G_1G_2=0,\cdots,G_iG_j=0(i \neq j)

$G_{1} G_{2} = 0, \dots, G_{i} G_{j} = 0 (i \neq = j)$

∵

G

1

G

2

=

(

Q

D

1

Q

−

1

)

(

Q

D

2

Q

−

1

)

=

0

\because G_1G_2=(QD_1Q^{-1})(QD_2Q^{-1})=0

$∵ G_{1} G_{2} = (Q D_{1} Q^{- 1}) (Q D_{2} Q^{- 1}) = 0$
G

1

2

=

G

1

,

⋯

,

G

k

2

=

G

k

G_1^2=G_1,\cdots,G_k^2=G_k

$G_{1}^{2} = G_{1}, \dots, G_{k}^{2} = G_{k}$ ，且

G

1

H

=

G

1

,

⋯

,

G

k

H

=

G

k

G_1^H=G_1,\cdots,G_k^H=G_k

$G_{1}^{H} = G_{1}, \dots, G_{k}^{H} = G_{k}$ 都是Hermite阵

b. 正规阵谱分解与谱阵性质

若

A=A_{n\times n}

$A = A_{n \times n}$ 正规，全体互异根为

⋯

\lambda_1,\cdots,\lambda_k

$λ_{1}, \dots, λ_{k}$ ，则有

⋯

A=\lambda_1G_1+\lambda_2G_2+\cdots+\lambda_kG_k

$A = λ_{1} G_{1} + λ_{2} G_{2} + \dots + λ_{k} G_{k}$ ，其中

⋯

G_1,\cdots,G_k

$G_{1}, \dots, G_{k}$ 为

$A$ 的谱阵

性质

①和为

：

⋯

②正交：

⋯

(

≠

)

③幂等：

⋯

(

幂等

)

且

⋯

④正规阵幂次：

⋯

⑤正规阵函数：

(

)

(

)

⋯

(

)

(

)

⋯

∵

(

)

⋯

(

⋯

)

(

⋯

)

⋯

(

⋯

)

(

)

(

⋯

)

⋯

(

⋯

)

(

)

⋯

(

)

⑥正规阵求法：设

正规，全体不同根为

⋯

，则有谱阵公式

⋯

(

−

)

⋯

(

−

)

(

−

)

⋯

(

−

)

(

−

)

(

−

)

⋯

(

−

)

(

−

)

(

−

)

⋯

(

−

)

⋯

(

−

)

(

−

)

⋯

(

−

)

(

−

)

(

−

)

⋯

(

−

)

⑦谱阵中列是

的特征向量：

⋯

∵

(

⋯

)

\begin{aligned} &①和为I：G_1+G_2+\cdots+G_k=I\\ &②正交：G_1G_2=0,\cdots,G_iG_j=0(i\neq j)\\ &③幂等： G_1^{2}=G_1,\cdots,G_k^{2}=G_k(幂等),且G_1^H=G_1,\cdots ,G_k^H=G_k\\ &④正规阵幂次：A^p=\lambda_1^pG_1+\cdots+\lambda_kG_k,p=0,1,2.\cdots\\ &⑤正规阵函数：f(A)=f(\lambda_1)G_1+\cdots+f(\lambda_k)G_k,f(x)=c_0+c_1x_1+\cdots+c_px^p\\ & \quad \because f(A)=c_0I+c_1A+\cdots+c_kA^p\\ & \quad \quad =c_0(G_1+\cdots+G_k)+c_1(\lambda_1G_1+\lambda_2G_2+\cdots+\lambda_kG_k)+\\ & \quad \quad \quad \cdots+c_p(\lambda_1^pG_1+\lambda_2^pG_2+\cdots+\lambda_p^kG_k)\\ & \quad \quad =(c_0+c_1\lambda_1+c_p\lambda_1^k)G_1+(c_0+c_1\lambda_2+\cdots+c_p\lambda_2^pk)G_2+\\ & \quad \quad \quad \cdots+(c_0+c_1\lambda_k+\cdots+c_p\lambda_k^p)G_k\\ & \quad \quad =f(\lambda_1)G_1+\cdots+f(\lambda_k)G_k\\ &⑥正规阵求法：设A正规，全体不同根为 \lambda_1,\lambda_2,\cdots,\lambda_k，则有谱阵公式G_1,G_2,\cdots,G_k\\ &\quad G_1=\frac{(A-\lambda_2I)\cdots(A-\lambda_kI)}{(\lambda_1-\lambda_2)\cdots(\lambda_1-\lambda_k)},G_2=\frac{(A-\lambda_1I)(A-\lambda_3I)\cdots(A-\lambda_kI)}{(\lambda_2-\lambda_1)(\lambda_2-\lambda_3)\cdots(\lambda_2-\lambda_k)}\\ &\quad\cdots\\ &\quad G_k=\frac{(A-\lambda_1I)(A-\lambda_2I)\cdots(A-\lambda_{k-1}I)}{(\lambda_k-\lambda_1)(\lambda_k-\lambda_2)\cdots(\lambda_k-\lambda_{k-1})}\\ &⑦谱阵中列是A的特征向量：AG_1=\lambda_1G_1,AG_2=\lambda_2G_2,\cdots,AG_k=\lambda_kG_k\\ &\quad \because AG_1=(\lambda_1G_1+\cdots+\lambda_kG_k)G_1=\lambda_1G_1 \end{aligned}

$① 和为 I ： G_{1} + G_{2} + \dots + G_{k} = I ② 正交： G_{1} G_{2} = 0, \dots, G_{i} G_{j} = 0 (i \neq = j) ③ 幂等： G_{1}^{2} = G_{1}, \dots, G_{k}^{2} = G_{k} (幂等), 且 G_{1}^{H} = G_{1}, \dots, G_{k}^{H} = G_{k} ④ 正规阵幂次： A^{p} = λ_{1}^{p} G_{1} + \dots + λ_{k} G_{k}, p = 0, 1, 2. \dots ⑤ 正规阵函数： f (A) = f (λ_{1}) G_{1} + \dots + f (λ_{k}) G_{k}, f (x) = c_{0} + c_{1} x_{1} + \dots + c_{p} x^{p} ∵ f (A) = c_{0} I + c_{1} A + \dots + c_{k} A^{p} = c_{0} (G_{1} + \dots + G_{k}) + c_{1} (λ_{1} G_{1} + λ_{2} G_{2} + \dots + λ_{k} G_{k}) + \dots + c_{p} (λ_{1}^{p} G_{1} + λ_{2}^{p} G_{2} + \dots + λ_{p}^{k} G_{k}) = (c_{0} + c_{1} λ_{1} + c_{p} λ_{1}^{k}) G_{1} + (c_{0} + c_{1} λ_{2} + \dots + c_{p} λ_{2}^{p} k) G_{2} + \dots + (c_{0} + c_{1} λ_{k} + \dots + c_{p} λ_{k}^{p}) G_{k} = f (λ_{1}) G_{1} + \dots + f (λ_{k}) G_{k} ⑥ 正规阵求法：设 A 正规，全体不同根为 λ_{1}, λ_{2}, \dots, λ_{k} ，则有谱阵公式 G_{1}, G_{2}, \dots, G_{k} G_{1} = \frac{( A - λ _{2} I ) \dots ( A - λ _{k} I )}{( λ _{1} - λ _{2} ) \dots ( λ _{1} - λ _{k} )}, G_{2} = \frac{( A - λ _{1} I ) ( A - λ _{3} I ) \dots ( A - λ _{k} I )}{( λ _{2} - λ _{1} ) ( λ _{2} - λ _{3} ) \dots ( λ _{2} - λ _{k} )} \dots G_{k} = \frac{( A - λ _{1} I ) ( A - λ _{2} I ) \dots ( A - λ _{k - 1} I )}{( λ _{k} - λ _{1} ) ( λ _{k} - λ _{2} ) \dots ( λ _{k} - λ _{k - 1} )} ⑦ 谱阵中列是 A 的特征向量： A G_{1} = λ_{1} G_{1}, A G_{2} = λ_{2} G_{2}, \dots, A G_{k} = λ_{k} G_{k} ∵ A G_{1} = (λ_{1} G_{1} + \dots + λ_{k} G_{k}) G_{1} = λ_{1} G_{1}$

谱阵求法

由推论⑤可知，取k个不同的函数f(x)可求出谱阵

⋯

G_1,G_2,\cdots.G_k

$G_{1}, G_{2}, \dots . G_{k}$

证明：

在这里插入图片描述

A正规有2个不同根

−

\begin{aligned} G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2},G_2=I-G_1=\frac{A-\lambda_1I}{\lambda_2-\lambda_1} \end{aligned}

$G_{1} = \frac{A - λ _{2} I}{λ _{1} - λ _{2}}, G_{2} = I - G_{1} = \frac{A - λ _{1} I}{λ _{2} - λ _{1}}$

A正规且有3个不同根

(

−

)

(

−

)

(

−

)

(

−

)

(

−

)

(

−

)

(

−

)

(

−

)

−

(

−

)

(

−

)

(

−

)

(

−

)

\begin{aligned} &G_1=\frac{(A-\lambda_2I)(A-\lambda_3I)}{(\lambda_1-\lambda_2)(\lambda_1-\lambda_3)},G_2=\frac{(A-\lambda_1I)(A-\lambda_3I)}{(\lambda_2-\lambda_1)(\lambda_2-\lambda_3)},\\ &G_3=I-G_1-G_2=\frac{(A-\lambda_1I)(A-\lambda_2I)}{(\lambda_3-\lambda_1)(\lambda_3-\lambda_2)} \end{aligned}

$G_{1} = \frac{( A - λ _{2} I ) ( A - λ _{3} I )}{( λ _{1} - λ _{2} ) ( λ _{1} - λ _{3} )}, G_{2} = \frac{( A - λ _{1} I ) ( A - λ _{3} I )}{( λ _{2} - λ _{1} ) ( λ _{2} - λ _{3} )}, G_{3} = I - G_{1} - G_{2} = \frac{( A - λ _{1} I ) ( A - λ _{2} I )}{( λ _{3} - λ _{1} ) ( λ _{3} - λ _{2} )}$

正规分解性质的应用例

1

(

−

)

(

实对称正规阵

)

，求

与

(

)

的谱分解，与

100

\begin{aligned} A=\left( \begin{matrix} 1&0&-2\\ 0&0&0\\ -2&0&4 \end{matrix} \right)(实对称正规阵)，求A与f(A)的谱分解，与A^{100} \end{aligned}

$A = 10 - 2 000 - 2 04 (实对称正规阵) ，求 A 与 f (A) 的谱分解，与 A^{100}$

可知

为秩

矩阵，

(

)

特征根为

(

)

不同根为

−

(

−

)

−

(

)

得谱分解：

且

(

)

(

)

(

)

即

(

)

(

)

(

)

令

(

)

100

⇒

100

(

)

(

)

100

由于

中列向量都是

的特征向量，所以

的特征向量

(

−

)

的特征向量

(

)

(

)

\begin{aligned} &可知A为秩1矩阵，r(A)=1,特征根为\lambda(A)={5,0,0},不同根为\lambda_1=5,\lambda_2=0\\ &G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=\frac{1}{5}\left( \begin{matrix} 1&0&-2\\ 0&0&0\\ -2&0&4 \end{matrix} \right),G_2=\frac{A-\lambda_1I}{\lambda_2-\lambda_1}=I-G_1=\frac{1}{5}\left( \begin{matrix} 4&0&2\\ 0&5&0\\ 2&0&1 \end{matrix} \right)\\ &得谱分解：A=\lambda_1G_1+\lambda_2G_2,且f(A)=f(\lambda_1)G_1+f(\lambda_2)G_2\\ &即f(A)=f(5)G_1+f(0)G_2\\ &令f(x)=x^{100}\Rightarrow A^{100}=f(5)G_1+f(0)G_2=5^{100}G_1=5^{100}\frac{1}{5}A=5^{99}A\\ &由于G中列向量都是A的特征向量，所以\lambda_1=5的特征向量\alpha_1=\left( \begin{matrix} 1\\0\\-2 \end{matrix} \right)\\ &\lambda_2=0的特征向量\alpha_2=\left( \begin{matrix} 2\\0\\1 \end{matrix} \right),\alpha_3=\left( \begin{matrix} 0\\1\\0 \end{matrix} \right) \end{aligned}

$可知 A 为秩 1 矩阵， r (A) = 1, 特征根为 λ (A) = 5, 0, 0, 不同根为 λ_{1} = 5, λ_{2} = 0 G_{1} = \frac{A - λ _{2} I}{λ _{1} - λ _{2}} = \frac{1}{5} 10 - 2 000 - 2 04, G_{2} = \frac{A - λ _{1} I}{λ _{2} - λ _{1}} = I - G_{1} = \frac{1}{5} 402050201 得谱分解： A = λ_{1} G_{1} + λ_{2} G_{2}, 且 f (A) = f (λ_{1}) G_{1} + f (λ_{2}) G_{2} 即 f (A) = f (5) G_{1} + f (0) G_{2} 令 f (x) = x^{100} \Rightarrow A^{100} = f (5) G_{1} + f (0) G_{2} = 5^{100} G_{1} = 5^{100} \frac{1}{5} A = 5^{99} A 由于 G 中列向量都是 A 的特征向量，所以 λ_{1} = 5 的特征向量 α_{1} = 10 - 2 λ_{2} = 0 的特征向量 α_{2} = 201, α_{3} = 010$

2

在这里插入图片描述

2.分块法

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QSnf9MdK-1671548454484)(2.矩阵分解/image-20221031231951042.png)]

c. 新平方根公式

⋯

条件：

正规，且

⋯

\begin{aligned} &\sqrt{A}=\sqrt{\lambda_1}G_1+\sqrt{\lambda_2}G_2+\cdots+\sqrt{\lambda_n}G_n\\ &条件：A正规，且A=\lambda_1G_1+\cdots+\lambda_kG_k \end{aligned}

$A = λ_{1} G_{1} + λ_{2} G_{2} + \dots + λ_{n} G_{n} 条件： A 正规，且 A = λ_{1} G_{1} + \dots + λ_{k} G_{k}$

证明：

(

)

(

⋯

)

⋯

\begin{aligned} (\sqrt{A})^2&=(\sqrt{\lambda_1}G_1+\sqrt{\lambda_2}G_2+\cdots+\sqrt{\lambda_k}G_k)^2\\ &=\lambda_1G_1^2+\lambda_2G_2^2+\cdots+\lambda_kG_k^2\\ &=\lambda_1G_1+\lambda_2G_2+\cdots+\lambda_kG_k \end{aligned}

$(A)^{2} = (λ_{1} G_{1} + λ_{2} G_{2} + \dots + λ_{k} G_{k})^{2} = λ_{1} G_{1}^{2} + λ_{2} G_{2}^{2} + \dots + λ_{k} G_{k}^{2} = λ_{1} G_{1} + λ_{2} G_{2} + \dots + λ_{k} G_{k}$

eg

(

)

求

A=\left( \begin{matrix} 5&4\\ 4&5 \end{matrix} \right),求\sqrt{A}

$A = (5445), 求 A$

由于

为行和相等矩阵，

∴

(

)

{

(

)

−

}

{

}

令

⇒

−

(

)

−

(

−

)

⇒

(

)

\begin{aligned} &由于A为行和相等矩阵，\therefore \lambda(A)=\{9,tr(A)-9\}=\{9,1\},令\lambda_1=9,\lambda_2=1\\ &\Rightarrow G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=\frac{1}{2}\left( \begin{matrix} 1&1\\1&1 \end{matrix} \right),G_2=\frac{A-\lambda_1I}{\lambda_2-\lambda_1}=\frac{1}{2}\left( \begin{matrix} 1&-1\\-1&1 \end{matrix} \right)\\ &\Rightarrow \sqrt{A}=\sqrt{\lambda_1}G_1+\sqrt{\lambda_2}G_2=3G_1+G_2=\left( \begin{matrix} 2&1\\1&2 \end{matrix} \right) \end{aligned}

$由于 A 为行和相等矩阵， ∴ λ (A) = {9, t r (A) - 9} = {9, 1}, 令 λ_{1} = 9, λ_{2} = 1 \Rightarrow G_{1} = \frac{A - λ _{2} I}{λ _{1} - λ _{2}} = \frac{1}{2} (1111), G_{2} = \frac{A - λ _{1} I}{λ _{2} - λ _{1}} = \frac{1}{2} (1 - 1 - 1 1) \Rightarrow A = λ_{1} G_{1} + λ_{2} G_{2} = 3 G_{1} + G_{2} = (2112)$

2.4.5 正规谱分解

a. 正规分解推导

b. 正规阵谱分解与谱阵性质

性质

谱阵求法

A正规有2个不同根

A正规且有3个不同根

正规分解性质的应用例

1

2

2.分块法

c. 新平方根公式

证明：

eg

你可能也喜欢