《图论及其应用》

主要考试知识点：

第2章，第 3章，第5 章，第 6章，章节占比：20%，25%，30%，25%。

**第2章：**图的定义、度的概念、握手定理、可图画、同构、子图、二部图及其判断、极大路径法、图的矩阵表示等、图的连通性等基本概念；欧拉图的概念 和判定定理，汉密尔顿图的概念和若干充分条件、必要条件；

**第3章：**树的概念和树的性质，生成树和生成树的计数，最小生成树；有向树、根树，最优二元树及最佳前缀码；最短路算法（如Dijkstra算法）；

**第5章：**独立集、支配集、独立数、支配数、覆盖数的概念以及关系，极大独立集、极小小支配集、最小点覆盖等概念、性质和布尔计算；匹配、最大匹配、 最优匹配及其匈牙利算法等；

**第 6 章:**平面图、平面图的度数、边界、极大平面图定义及相关性质，对偶图的概念和基本性质；Euler公式及其推论、平面图的判断定理、平面图的着色、
色多项式、色数问题等。

**重点：**图的相关概念，度与边数间的关系，图的同构，欧拉图的判别和汉密尔顿图的必要条件和充分性，树的等价命题，最优生成树，最优前缀码的构造， 最短路径求法，最短路径问题，极大独立集，极小点覆盖，极小支配集等的布尔运算、Hall定理、匈牙利算法的应用、最优匹配、欧拉公式、色多项式等。

简单题、中等难度题：较难题：难题的比例为：30%:40%:20%:10%.

题型：选择题(15 分)、填空题(15分)，作图解答题(18 分)、计算题(40分)和证明题(12 分)等。

不考内容：竞赛图、货郎担问题、树的遍历、定义3.3.10到3.4节之间内容、92-99页、129页的矩阵的平移变换、6.4节等等。

第2章：

图的定义：

无向图 (undirected graph)是一个序偶 ⟨𝑉 , 𝐸⟩，记作 𝐺 = ⟨𝑉 , 𝐸⟩，其中
• 𝑉 是非空集合，称为 𝐺 的结点集 (vertex set)，𝑉 中元素称为点或结点 (vertex)；
• 𝐸 是无序积 𝑉 &𝑉 的多重子集（元素可重复出现的集合），称为 𝐺 的边集 (edge set)，𝐸 中元素称为无向边 (undirected edge)或简称边 (edge)．

• 为了表示 𝑉 和 𝐸 分别是图 𝐺 的结点集和边集，常将 𝑉 记作 𝑉 (𝐺)，将 𝐸 记成 𝐸(𝐺)

有向图 (directed graph or digraph)是一个序偶 ⟨𝑉 , 𝐸⟩，记作 𝐺 = ⟨𝑉 , 𝐸⟩．其中：
• 𝑉 是非空点集；
• 𝐸 是笛卡尔积 𝑉 × 𝑉 的多重子集，𝐸 中元素称为有向边 (directed edges)，也简称为边或弧 (arc)．
• 一般的，有向图用 𝐷 表示，如 𝐷 = ⟨𝑉 , 𝐸⟩．

给图的结点和边都标记名称的图称为标定图．

• 若边 𝑒 = (𝑢, 𝑣)，称 𝑢, 𝑣 为 𝑒 的端点 (endpoint)，并称 𝑒 与 𝑢 和 𝑣 是关联的 (incident)(边与点)，而称结点 𝑢 与 𝑣 是邻接的 (adjacent)(点与点)
• 若 𝑒 = ⟨𝑢, 𝑣⟩，称 𝑢 为 𝑒 的始点 (initial vertex)，𝑣 为 𝑒 的终点 (terminal vertex)．
• 若两条边关联于同一结点，则称两边是相邻(边与边)的 (adjacent)．
• 无边关联的结点称为孤立点 (isolated vertex)．
• 若一条边关联的两个结点重合，则称为环或回路 (loop)．

• 若 𝑒 = (𝑢, 𝑣) 且 𝑢 ≠ 𝑣 时，称 𝑒 与 𝑢（或 𝑣）的关联次数为 1．
• 若 𝑒 = (𝑢, 𝑢)，称 𝑒 与 𝑢 的关联次数为 2．
• 若 𝑢 不是 𝑒 的端点，𝑒 与 𝑢 的关联次数为 0．

设图 𝐺 = ⟨𝑉 , 𝐸⟩，
• 若 𝑉 和 𝐸 都是有限集，则称 𝐺 为有限图 (finite graph)，反之称为无限图 (infinite graph)．
• 若 |𝑉 | = 𝑛，则称 𝐺 为 𝑛 阶图 (𝑛-order graph)．
• 若 |𝑉 | = 𝑛, |𝐸| = 0, 则称 𝐺 为 𝑛 阶零图 (null graph)．
• 若 |𝑉 | = 1, |𝐸| = 0，则称 𝐺 为平凡图 (trivial graph)．

• 关联于同一对结点的多条边（有向边应同向）称为平行边．
• 平行边的条数称为边的重数 (multiplicity)．
• ⭐不含平行边和环的图称为简单图 (simple graph)．

⭐度的概念：

对于图 𝐺 = ⟨𝑉 , 𝐸⟩，𝑣 ∈ 𝑉 ，与 𝑣 关联的边的次数称为 𝑣 的度数 (degree)，简称度，记作 deg(𝑣)， 简记为 𝑑(𝑣)．
• 若 deg(𝑣) 为奇数，则称 𝑣 为奇点或奇度结点 (odd vertex)；
• 若 deg(𝑣) 为偶数，则称 𝑣 为偶点或偶度结点 (even vertex)．

称 Δ(𝐺) = max{deg(𝑣) ∣ 𝑣 ∈ 𝑉 } 为图 𝐺 的最大度 (maximum degree)；
称 𝛿(𝐺) = min{deg(𝑣) ∣ 𝑣 ∈ 𝑉 } 为图 𝐺 的最小度 (minimum degree)．

对于有向图 𝐷 = ⟨𝑉 , 𝐸⟩，𝑣 ∈ 𝑉 ，
• 𝑣 作为始点的次数，称为 𝑣 的出度 (out-degree)，记作 deg+ (𝑣)，简记为 𝑑+ (𝑣)；
• 𝑣 作为终点的次数，称为 𝑣 的入度 (in-degree)，记作 deg− (𝑣)，简记为 𝑑− (𝑣)．
显然，deg(𝑣) = deg+(𝑣) + deg−(𝑣)．

度为 1 的结点称为悬挂点 (pendant vertex)，与悬挂点关联的边称为悬挂边 (pendant edge)．

设 𝑉 = {𝑣1, 𝑣2 , … , 𝑣𝑛 } 为图 𝐺 的结点集，称 (deg(𝑣1 ), deg(𝑣2 ), … , deg(𝑣𝑛 )) 为 𝐺 的度序列 (degree sequence)．

⭐握手定理：

度数之和等于边数目的两倍（计算 𝐺 中各结点度数之和时，每条边均提供 2 度，故 𝑚 条边共提供 2𝑚 度．）

设图 𝐺 = ⟨𝑉 , 𝐸⟩ 有结点集 𝑉 = {𝑣1 , 𝑣2 , … , 𝑣𝑛 }，且边数 |𝐸| = 𝑚，则 ∑ deg(𝑣𝑖 ) = 2𝑚．

有向图出度之和等于入度之和等于m（每条有向边，包括环，均有一个始点和一个终点，所以在 𝐺 中的每条边都提供一个 出度和一个入度，说明 𝐺 中各结点的出度之和等于入度之和）

设有向图 𝐺 = ⟨𝑉 , 𝐸⟩ 有结点集 𝑉 = {𝑣1 , 𝑣2 , … , 𝑣𝑛 }，且边数 |𝐸| = 𝑚，则∑ deg+(𝑣𝑖) = ∑ deg−(𝑣𝑖 ) = 𝑚.

任意图中，奇度结点的个数必为偶数．

(设 𝑉1 = {𝑣 ∣ 𝑣 是奇度结点}，𝑉2 = {𝑣 ∣ 𝑣 是偶度结点}，则∑ deg(𝑣) + ∑ deg(𝑣) = ∑ = 2𝑚.由于 ∑deg(𝑣) 是偶数，且 2𝑚 是偶数，所以 ∑deg(𝑣) 也是偶数．注意到 𝑉1 中每个点 𝑣的度 deg(𝑣) 均是奇数，因此 |𝑉1 | 必为偶数．)

可图画:

设 𝐺 = ⟨𝑉 , 𝐸⟩ 是无向简单图，若任意两个结点之间都有边相连，则称 𝐺 为完全图 (complete graph)．具有 𝑛 个结点的完全图记作 **𝐾𝑛 ．**完全图的边数n(n-1)/2

设 𝐷 = ⟨𝑉 , 𝐸⟩ 是有向简单图，若任意两个结点之间都有一对方向相反的边相连，则称 𝐷 为有向完全图 (complete directed graph)．具有 𝑛 个结点的有向完全图记作 𝐷𝑛 ．边数n(n-1)

设 𝐷 = ⟨𝑉 , 𝐸⟩ 是有向简单图，若任意两个结点之间都有一条边相连，则称 𝐺 为竞赛图 (tournament (graph))。边数n(n-1)/2

⭐在一个无向简单图中，若每个结点的度数均为 𝑘, 则该图称为𝑘− 正则图 (𝑘−regular graph)．完全图 𝐾𝑛 是 (𝑛 − 1)− 正则图．

⭐给定一个简单图 𝐺，以 𝐺 中所有结点为结点集，以所有能使 𝐺 成为完全图所添加的边为边集组成的图，称为图 𝐺 相对于完全图的补图，简称 𝐺 的补图 (complementary graph)，记作 𝐺一把．

子图：

设 𝐺 = ⟨𝑉 , 𝐸⟩，𝐺′ = ⟨𝑉 ′ , 𝐸′ ⟩ 是两个图．若 𝑉 ′ ⊆ 𝑉 ，且 𝐸′ ⊆ 𝐸，则称 𝐺′ 是 𝐺 的 子图 (subgraph)，𝐺 是 𝐺′ 的母图 (supergraph)，记作 𝐺′ ⊆ 𝐺．

• 如果 𝐺′ ⊆ 𝐺，且 𝑉 ′ ⊂ 𝑉 或 𝐸′ ⊂ 𝐸，则称 𝐺′ 是 𝐺 的真子图 (proper subgraph)．

⭐如果 𝐺′ ⊆ 𝐺 且 𝑉 ′ = 𝑉 ，则称 𝐺′ 是 𝐺 的生成子图 (spanning subgraph)．(是子图并且点集等于母图点集)

若 𝑉 ′ ⊆ 𝑉 且 𝑉 ′ ≠ ∅，以 𝑉 ′ 为结点集，以图 𝐺 中两个端点均在 𝑉 ′ 中的边为边集的子图，称为 由 𝑉 ′ 导出的点导出子图 (vertex-induced subgraph)，简称导出子图 (induced subgraph)，记作 𝐺[𝑉 ′]．

若 𝐸 ′ ⊆ 𝐸 且 𝐸 ′ ≠ ∅，以 𝐸′ 为边集，以 𝐸′ 中关联的结点为结点集的子图，称为由 𝐸′ 导出的边导出子图 (edge-induced subgraph)，记作 𝐺[𝐸′ ]．

⭐图的同构：

给定图 𝐺 = ⟨𝑉 , 𝐸⟩ 和 𝐺′ = ⟨𝑉 ′ , 𝐸′ ⟩，如果存在双射 𝑔 ∶ 𝑉 → 𝑉 ′ ，使得 (𝑢, 𝑣) ∈ 𝐸 当且仅当 (𝑔(𝑢), 𝑔(𝑣)) ∈ 𝐸 ′（或 ⟨𝑢, 𝑣⟩ ∈ 𝐸 当且仅当 ⟨𝑔(𝑢), 𝑔(𝑣)⟩ ∈ 𝐸′ ），且重数相同，则称图 𝐺 与图 𝐺′ 同构 (isomorphic)，记为 𝐺 ≅ 𝐺′ ．(可以理解为一切关系相同，可以用相同的数学记法表示 ，可以联系到网络科学中，生活中很多不同的网络，可能对应着一张图)

两图同构的必要条件：
• 结点数相同，即 |𝑉 | = |𝑉 ′ |．
• 边数相同，即 |𝐸| = |𝐸′ |．
• 对应点的度数相同，即 deg(𝑣) = deg(𝑔(𝑣)), 𝑣 ∈ 𝑉 ．
同构的两个图的顶点之间，具有保持相邻关系的一一对应．

图的运算*(非重点)：

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为无向图．
1 设 𝑒 ∈ 𝐸，从 𝐺 中去掉边 𝑒，称为删除 𝑒，用 𝐺 − 𝑒 表示删除 𝑒 后的子图．
2 设 𝐸 ′ ⊆ 𝐸，从 𝐺 中删除 𝐸′ 中所有的边，称为删除 𝐸′ ，用 𝐺 − 𝐸′ 表示删除 𝐸′ 后的子图．

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为无向图．
1 设 𝑣 ∈ 𝑉 ，从 𝐺 中去掉点 𝑣 及所关联的一切边，称为删除 𝑣，用 𝐺 − 𝑣 表示删除 𝑣 后的子图．
2 设 𝑉 ′ ⊆ 𝑉 ，从 𝐺 中删除 𝑉 ′ 中所有的结点，称为删除 𝑉 ′ ，用 𝐺 − 𝑉 ′ 表示删除 𝑉 ′ 后的子图．

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为无向图．设边 𝑒 = (𝑢, 𝑣) ∈ 𝐸，先从 𝐺 中删除 𝑒，再将 𝑒 的两个端点 𝑢, 𝑣 用一个 新的结点 𝑤（或用 𝑢 或 𝑣 充当 𝑤）代替，使 𝑤 关联除 𝑒 以外 𝑢, 𝑣 关联的一切边，称为收缩边 𝑒， 并用 𝐺\𝑒 表示所得新图．

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为无向图．设 𝑢, 𝑣 ∈ 𝑉 且 𝑢 ≠ 𝑣，在 𝑢, 𝑣 之间加新边 (𝑢, 𝑣)，称为加新边，并用 𝐺 ∪ (𝑢, 𝑣) 或 𝐺 + (𝑢, 𝑣) 表示所得新图．

图的连通性：

给定图 𝐺 = ⟨𝑉 , 𝐸⟩，设 𝑣0 , 𝑣1 , … , 𝑣𝑛 ∈ 𝑉 ，𝑒1 , 𝑒2 , … , 𝑒𝑛 ∈ 𝐸，其中对 1 ≤ 𝑖 ≤ 𝑛，𝑒𝑖 = (𝑣𝑖−1 , 𝑣𝑖 )（或 𝑒𝑖 = ⟨𝑣𝑖−1 , 𝑣𝑖 ⟩），称点边交错序列𝑣0𝑒1𝑣1𝑒2𝑣2 … 𝑣𝑛−1 𝑒𝑛 𝑣𝑛为结点 𝑣0 到 𝑣𝑛 的通路或途径．其中 𝑣0 和 𝑣𝑛 分别称为通路的起点和终点，边数 𝑛 称为通路 的长度．若 𝑣0 = 𝑣𝑛 ，则称该通路为回路．

• 若通路中的边 𝑒1, 𝑒2, … , 𝑒𝑛 互不相同，则称该通路为简单通路．
• 若回路中的边 𝑒1, 𝑒2, … , 𝑒𝑛 互不相同，则称该回路为简单回路．
• 若通路中的点 𝑣0, 𝑣1, … , 𝑣𝑛 互不相同，则称该通路为路径．

若简单回路中除起点和终点外的所有结点互不相同，则称为圈 (cycle)，长度为 𝑘 的圈称为𝑘 圈．

• 长度为奇数的圈称为奇圈 (odd cycle)．
• 长度为偶数的圈称为偶圈 (even cycle)．

给定 𝑛 阶图 𝐺，若从结点 𝑣𝑖 到 𝑣𝑗 (𝑣𝑖 ≠ 𝑣𝑗 ) 存在一条通路，则从 𝑣𝑖 到 𝑣𝑗 中存在一条长度小于或 等于 𝑛 − 1 的通路．

给定 𝑛 阶图 𝐺，若从结点 𝑣𝑖 到 𝑣𝑗 (𝑣𝑖 ≠ 𝑣𝑗 ) 存在一条通路，则从 𝑣𝑖 到 𝑣𝑗 中存在一条长度小于或 等于 𝑛 − 1 的路径．

给定 𝑛 阶图 𝐺，
• 若存在 𝑣𝑖 到自身的回路，则一定存在 𝑣𝑖 到自身长度小于或等于 𝑛 的回路．
• 若存在 𝑣𝑖 到自身的简单回路，则一定存在 𝑣𝑖 到自身长度小于或等于 𝑛 的圈．

在无向图 𝐺 = ⟨𝑉 , 𝐸⟩ 中，若存在从结点 𝑣𝑖 到 𝑣𝑗 (𝑣𝑖 ≠ 𝑣𝑗 ) 的通路，则称 𝑣𝑖 与 𝑣𝑗 是连通的(connected)，记作 𝑣𝑖 ∼ 𝑣𝑗 ．规定任意结点 𝑣𝑖 与自身是连通的，即 𝑣𝑖 ∼ 𝑣𝑖 ．

若无向图 𝐺 中任意两个结点都是连通的，则称图 𝐺 是连通图 (connected graph)．规定平凡图是连通图．

⭐设 𝐺 = ⟨𝑉 , 𝐸⟩ 为无向图，如果 𝑉 上的连通关系将 𝑉 划分为 𝑘(𝑘 ≥ 1) 个等价类 𝑉1 , 𝑉2 , … , 𝑉𝑘 ， 则称它们的导出子图 𝐺[𝑉1 ], 𝐺[𝑉2 ], … , 𝐺[𝑉𝑘 ] 为 𝐺 的连通分支 (connected component)，其中连通分支的个数 𝑘 记为 𝜔(𝐺)．(一个图可以划分成几个连通的子图)

• 若 𝐺 为连通图，则 𝜔(𝐺) = 1；若 𝐺 为非连通图，则 𝜔(𝐺) ≥ 2．
• 在所有的 𝑛 阶无向图中，连通分支最多的图为 𝑛 阶零图，其 𝜔(𝐺) = 𝑛．

有向图两个节点a到b之间有通路(单向的)，则两节点可达(若 b到a也有则相互可达)，并且自身总是可达自身

• 可达“→”不是 𝑉 上的等价关系．
• 相互可达“↔”是 𝑉 上的等价关系．

在图 𝐺 = ⟨𝑉 , 𝐸⟩ 中，从结点 𝑣𝑖 到 𝑣𝑗 的最短通路称为 𝑣𝑖 到 𝑣𝑗 的短程线，短程线的长度称为 𝑣𝑖到 𝑣𝑗 的距离 (distance)(最短通路长度)，记作 **𝑑(𝑣𝑖 , 𝑣𝑗 )．**若 𝑣𝑖 到 𝑣𝑗 不存在通路，则规定 𝑑(𝑣𝑖 , 𝑣𝑗 ) = ∞．

有向连通图

• 弱连通图 (weakly connected graph)：
若去掉有向图 𝐷 中各边的方向后所得的无向图 𝐺 是连通的．(两点之间可能不连通)
• 单向连通图 (unilaterally connected graph)：
若有向图 𝐷 中任意两个结点 𝑣𝑖 , 𝑣𝑗 之间，或者 𝑣𝑖 可达 𝑣𝑗 或者 𝑣𝑗 可达 𝑣𝑖 ．(两点至少存在一条单向通路)
• 强连通图 (strongly connected graph)：
若有向图 𝐷 中任意两个结点之间都互相可达．

• 若 𝐷 是单向连通图，则 𝐷 一定是弱连通图．
• 若 𝐷 是强连通图，则 𝐷 一定是单向连通图，也一定是弱连通图．

⭐𝑛 阶有向图 𝐷 是强连通图 当且仅当 𝐷 中存在一条经过每个结点至少一次的回路．

充分性．如果图 𝐷 存在一条回路，它至少经过每个结点一次，则 𝐷 中任意两个结点相互可达，故 𝐷 是强连通的．
必要性．设 𝑉 (𝐷) = {𝑣1 , 𝑣2 , ⋯ , 𝑣𝑛 }．由于 𝐷 是强连通的，则 𝑣𝑖 → 𝑣𝑖+1 (1 ≤ 𝑖 ≤ 𝑛 − 1)．设 𝑝𝑖 为 𝑣𝑖 到 𝑣𝑖+1 的通路．又因为 𝑣𝑛 → 𝑣1 ，设 𝑝𝑛 为 𝑣𝑛 到 𝑣1 的通路．则 𝑝1 , 𝑝2 , … , 𝑝𝑛−1 , 𝑝𝑛 所组成的回 路经过 𝐷 中的每个结点至少一次．

⭐𝑛 阶有向图 𝐷 是单向连通的当且仅当 𝐷 中存在一条经过每个结节至少一次的通路．

无向连通图

设无向图 𝐺 = ⟨𝑉 , 𝐸⟩，若存在 𝑉 ′ ⊆ 𝑉 且 𝑉 ′ ≠ ∅，使得 𝜔(𝐺 − 𝑉 ′ ) > 𝜔(𝐺)，而对任意 𝑉 ″ ⊂ 𝑉 ′ ，都有 𝜔(𝐺 − 𝑉 ″) = 𝜔(𝐺)(点割集中不能出现割点。)，则称 𝑉 ′ 是 𝐺 的点割集 (vertex-cut set)．若 𝑉 ′ = {𝑣} 为单点集，则称𝑣 为割点 (cut vertex)．（去除这些点后，图变得更加不连通。但是去除这些点的子集连通情况不变）

设 𝐺 为无向连通图且为非完全图，则称 𝜅(𝐺) = min{|𝑉 ′ | ∣ 𝑉 ′ 为 𝐺 的点割集} 为 𝐺 的点连通度 (vertex connectivity)，简称连通度 (connectivity)．若 𝜅(𝐺) ≥ 𝑘，则称 𝐺 为 𝑘− 连通图 (𝑘−connected graph)．(使无向连通图变得不连通所要去除的最少节点个数)

• 规定平凡图的连通度为 0；规定完全图 𝐾𝑛 的连通度为 𝑛 − 1．
• 非连通图的连通度为 0．
• 存在割点的连通图的连通度为 1．
• 𝑘− 连通图中任意删除 𝑘 − 1 个结点后仍然连通．

设无向图 𝐺 = ⟨𝑉 , 𝐸⟩，若存在 𝐸′ ⊆ 𝐸 且 𝐸′ ≠ ∅，使得 𝜔(𝐺 − 𝐸′ ) > 𝜔(𝐺)，而对任意 𝐸″ ⊂ 𝐸′ ，都有 𝜔(𝐺 − 𝐸 ″) = 𝜔(𝐺)，则称 𝐸′ 是 𝐺 的边割集 (edge-cut set)．若 𝐸′ = {𝑒} 为单点集，则称 𝑒为割边 (cut edge)或桥 (bridge)．（去除这些边后，图变得更加不连通。但是去除这些边的子集连通情况不变）

设 𝐺 为无向图连通图，则称 𝜆(𝐺) = min{|𝐸′ | ∣ 𝐸′ 为 𝐺 的边割集} 为 𝐺 的边连通度 (edge connectivity)．若 𝜆(𝐺) ≥ 𝑟，则称 𝐺 为 𝑟− 边连通图 (𝑟−edge−connected graph)．(使无相连通图变得不连通所要去除的最少边个数)

• 规定平凡图的边连通度为 0．
• 非连通图的边连通度为 0．
• 存在割边的连通图的边连通度为 1．
• 𝑘− 边连通图中任意删除 𝑘 − 1 条边后仍然连通．

对于任何无向图 𝐺 = ⟨𝑉 , 𝐸⟩，有 𝜅(𝐺) ≤ 𝜆(𝐺) ≤ 𝛿(𝐺)．(连通度<=边连通度<=最小度)

⭐设 𝐺 = ⟨𝑉 , 𝐸⟩ 为无向连通图，则结点 𝑣 是割点当且仅当存在结点 𝑢 和 𝑤，使得连接 𝑢 和 𝑤 的每条通路都经过 𝑣.(去除v后u与w就不连通了)

⭐设 𝐺 = ⟨𝑉 , 𝐸⟩ 为无向连通图，则边 𝑒 是割边当且仅当存在结点 𝑢 和 𝑤，使得连接 𝑢 和 𝑤 的每条通路都经过 𝑒．

⭐设 𝐺 = ⟨𝑉 , 𝐸⟩ 为无向连通图，则边 𝑒 是割边的充分必要条件是 𝑒 不包含在 𝐺 的任何简单回路中。

必要性．设 𝑒 = (𝑢, 𝑣) 为 𝐺 的割边，假设 𝑒 在 𝐺 的简单回路 𝑢𝑒𝑣𝑒′ … 𝑒″ 𝑢 中．则在 𝐺 − 𝑒 中存在 一条连接 𝑢, 𝑣 的通路 𝑣𝑒′ … 𝑒″ 𝑢，于是 𝐺 − 𝑒 为连通图，与 𝑒 为割边矛盾．
充分性．设边 𝑒 = (𝑢, 𝑣) 不包含在 𝐺 的任何简单回路中．下证 𝑒 是割边．假设 𝑢, 𝑣 在 𝐺 − 𝑒 中连 通，则 𝐺 − 𝑒 中存在路径 𝑢𝑒′ … 𝑒″ 𝑣．于是 𝑢𝑒′ … 𝑒″ 𝑣𝑒𝑢 为 𝐺 中的一条简单回路，与条件矛盾．故 𝑢, 𝑣 在 𝐺 − 𝑒 中不连通，即 𝑒 为 𝐺 的割边

极大路径法:

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为 𝑛 阶无向图，Γ𝑙 为 𝐺 中一条 𝑙 长的路径，若此路径的始点或终点与路径外的结点相邻，则将邻点扩充到路径中来，继续这一过程，直到路径的始点和终点不与路径外的结点相邻为止．设最后得到的 𝑙 + 𝑘 长路径为 Γ𝑙+𝑘 ，称 Γ𝑙+𝑘 为极大路径，称此方法为扩大路径法．

⭐设 𝐺 为 𝑛(𝑛 ≥ 4) 阶无向简单图，𝛿(𝐺) ≥ 3，则 𝐺 中存在长度大于或等于 4 的圈．

二部图及其判断:

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为无向图，若存在 𝑉 的划分 𝑉1 , 𝑉2 ，使得 𝐺 中任意的两个端点都分别属于 𝑉1 和𝑉2，则称 𝐺 为二部图 (bipartite graph)（或二分图，偶图等），称 𝑉1 和 𝑉2 为互补结点子集．常将二部图 𝐺 记为二部划分形式 ⟨𝑉1 , 𝑉2 , 𝐸⟩．(v1内与v2内所有点都不邻接)

称 ⟨𝑉1, 𝑉2, 𝑉1 &𝑉2 ⟩ 为完全二部图 (complete bipartite graph)，记为 𝐾𝑟,𝑠 ，其中 |𝑉1 | = 𝑟，|𝑉2 | = 𝑠

⭐无向图 𝐺 是二部图当且仅当 𝐺 中不含奇圈．(长度为奇数的圈，节点数也为奇数，不能二分)

图的矩阵表示：

关联矩阵

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为无向图，𝑉 = {𝑣1 , 𝑣2 , … , 𝑣𝑛 }，𝐸 = {𝑒1 , 𝑒2 , … , 𝑒𝑚 }，令𝑚𝑖𝑗 = 0, 若 𝑣𝑖 与 𝑒𝑗 不关联; 1, 若 𝑣𝑖 是 𝑒𝑗 的端点; 2, 若 𝑒𝑗 是 𝑣𝑖 上的环.称矩阵 (𝑚𝑖𝑗)𝑛×𝑚 为图 𝐺 的关联矩阵 (incidence matrix)，记为 𝑴 (𝐺)． 𝑚𝑖𝑗 计数的是结点 𝑣𝑖 与边 𝑒𝑗 关联的次数．

无环有向图的关联矩阵mij不关联为0，关联的话看i，i是起点为1,终点为-1.记为 𝑴 (𝐷)．

邻接矩阵

设 𝐷 = ⟨𝑉 , 𝐸⟩ 为有向图，𝑉 = {𝑣1 , 𝑣2 , … , 𝑣𝑛 }，令𝑎𝑖𝑗= 𝑘, 若从 𝑣𝑖 到 𝑣𝑗 的边有 𝑘 条; 0,若没有 𝑣𝑖 到 𝑣𝑗 的边. 称矩阵 (𝑎𝑖𝑗 )𝑛×𝑛 为图 𝐷 的邻接矩阵(adjacency matrix)，记为 𝑨(𝐷)，简记为 𝑨.

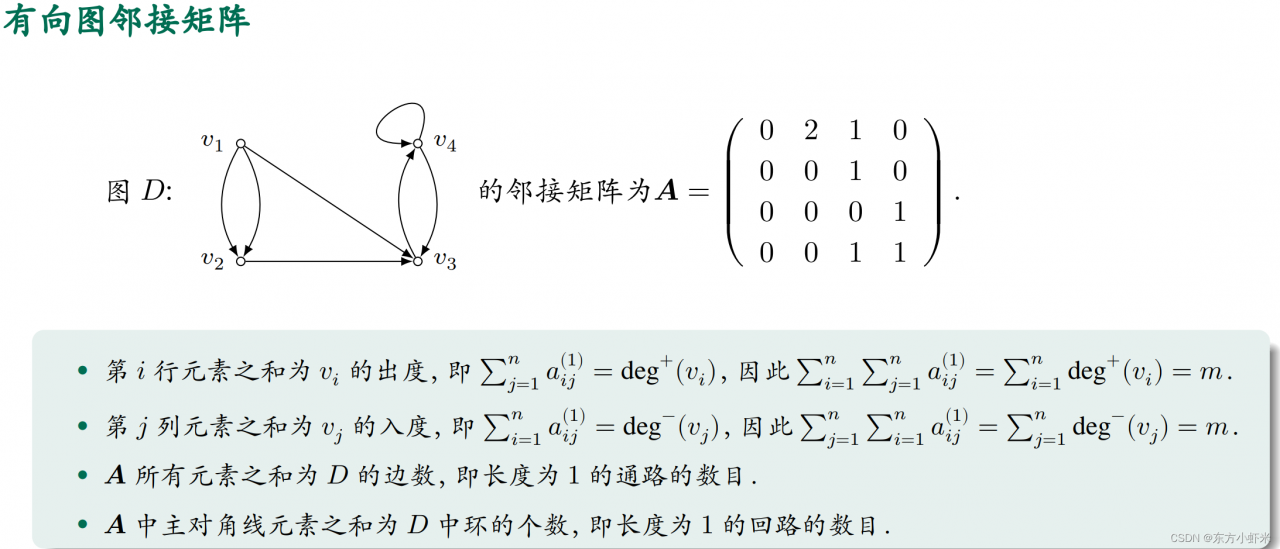
⭐设 𝐷 = ⟨𝑉 , 𝐸⟩ 为 𝑛 阶有向图，𝑉 = {𝑣1 , 𝑣2 , … , 𝑣𝑛 }，其邻接矩阵为 𝑨，则 𝑨^𝑘 (𝑘 = 1, 2, …) 中的(𝑖, 𝑗) 元 𝑎𝑖𝑗^(𝑘) 等于从结点 𝑣𝑖 到结点 𝑣𝑗 的长度为 𝑘 的通路的数目．

⭐设 𝐷 = ⟨𝑉 , 𝐸⟩ 为 𝑛 阶有向图，𝑉 = {𝑣1 , 𝑣2 , … , 𝑣𝑛 }，其邻接矩阵为 𝑨．对任意正整数 𝑟，令𝑩𝑟 = 𝑨 + 𝑨2 + ⋯ + 𝑨𝑟 = (𝑏𝑖𝑗^(𝑟) 则𝑏𝑖𝑗 ^(𝑟)表示从结点 𝑣𝑖 到结点 𝑣𝑗 的长度小于或等于 𝑟 的通路的总数，其中 𝑏𝑖𝑖 ^(𝑟)表示经过 𝑣𝑖 的长度小于或等于 𝑟 的回路的总数．

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为无向简单图，𝑉 = {𝑣1 , 𝑣2 , … , 𝑣𝑛 }，属于一条边则为1否则为0 。邻接矩阵 (adjacency matrix)，记为 𝑨(𝐺)，简记为 𝑨.

• 𝑨 为对称 0 − 1 矩阵，且主对角线元素均为 0．
• 第 𝑖 行（列）元素之和为 𝑣𝑖 的度．
• 𝑨 所有元素之和为 𝐺 中边数的两倍．

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为 𝑛 阶无向简单图，𝑉 = {𝑣1 , 𝑣2 , … , 𝑣𝑛 }，其邻接矩阵为 𝑨，则 𝑨𝑘 (𝑘 = 1, 2, …)中的 (𝑖, 𝑗) 元 𝑎^(𝑘)𝑖𝑗 等于从结点 𝑣𝑖 到结点 𝑣𝑗 的长度为 𝑘 的通路的数目．第二个推论bij也一样。

可达矩阵

两节点之间可达为1否则为0 可达矩阵 (reachability matrix)，记为 𝑷 (𝐷)，简记为 𝑷 .

可达矩阵的计算

为什么要加单位矩阵 𝑬？为什么只需要加到 𝑨𝑛−1 ？对角线自己一定可达自己,不存在长度为n的路径 最多只有n-1条边

可达矩阵是布尔矩阵，我们只关心两点之间是否存在通路，而不关心通过的长度及数目，所以我们可以对矩阵进行布尔运算．𝑷 = 𝑬 ∨ 𝑨 ∨ 𝑨^(2) ∨ 𝑨^(3) ……

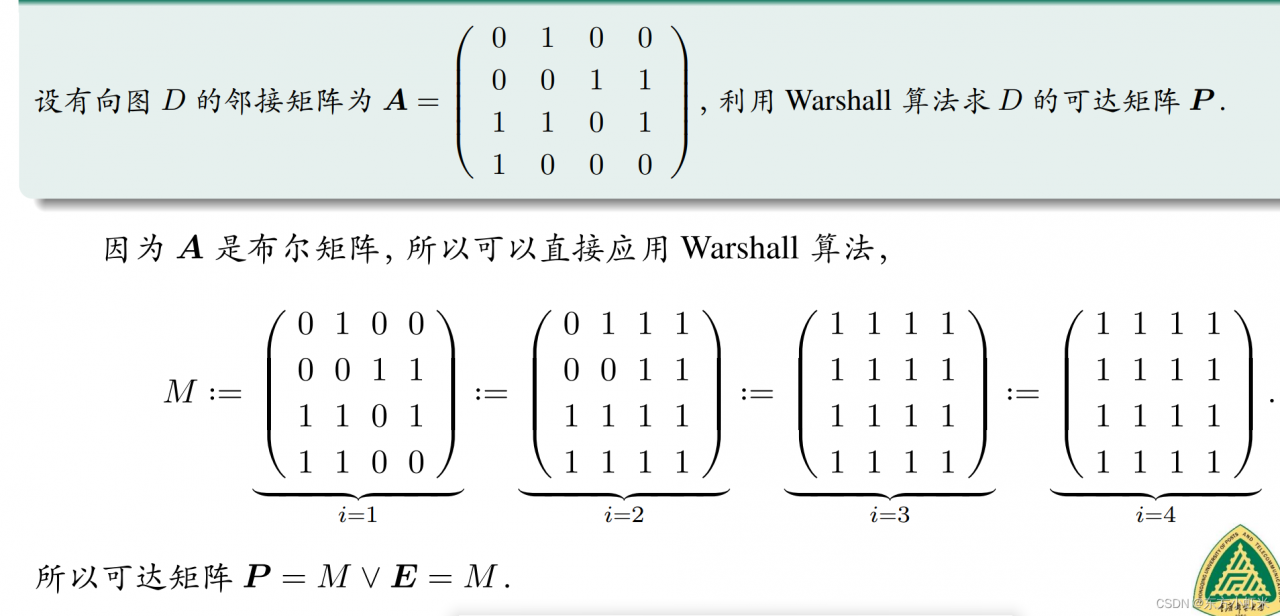
Warshall 算法计算可达矩阵．

设 𝑨 为有向图 𝐷 的邻接矩阵，
Step 1 将邻接矩阵 𝑨 转化为对应的布尔矩阵 𝑀 ；
Step 2 对布尔矩阵 𝑀 应用 Warshall 算法求得布尔矩阵 𝑀 ′
Step 3 可达矩阵 𝑷 ∶= 𝑀 ′ ∨ 𝑬．

⭐欧拉图的概念和判定定理:

柯尼斯堡七桥问题 最多智能有两个奇数度的节点(起点与终点)

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为无向图，
• 经过图 𝐺 的所有边一次且仅一次的回路称为欧拉回路，存在欧拉回路的图称为欧拉图 (Eulerian graph)．
• 经过图 𝐺 的所有边一次且仅一次的通路称为欧拉路，存在欧拉路而无欧拉回路的图称为半欧拉图 (semi-Eulerian graph)．

欧拉图和半欧拉图中除孤立点外是连通的．

⭐无向连通图 𝐺 = ⟨𝑉 , 𝐸⟩ 为欧拉图，当且仅当 𝐺 中无奇度结点．(可以理解一个点有奇数个节点的话，走出去为走进来为一对，那么总会有落单的一个)

⭐无向连通图 𝐺 = ⟨𝑉 , 𝐸⟩ 为半欧拉图，当且仅当 𝐺 中只有两个奇度结点．(而且这两点在欧拉路中是起点与终点)

设 𝐷 = ⟨𝑉 , 𝐸⟩ 为有向图，
• 经过图 𝐷 的所有边一次且仅一次的回路称为有向欧拉回路，存在有向欧拉回路的图称为有向欧拉图 (Eulerian digraph)．
• 经过图 𝐺 的所有边一次且仅一次的通路称为有向欧拉路，存在有向欧拉路而无有向欧拉回路的图称为有向半欧拉图 (semi-Eulerian digraph)．

连通的有向欧拉图一定是强连通的．(都经过所有边了，所有点也就都经过了)

⭐有向连通图 𝐷 = ⟨𝑉 , 𝐸⟩ 为有向欧拉图，当且仅当 𝐷 中所有结点的出度等于入度．

⭐有向连通图 𝐷 = ⟨𝑉 , 𝐸⟩ 为有向半欧拉图，当且仅当存在 𝑢, 𝑣 ∈ 𝑉 使得
1 deg+(𝑢) = deg−(𝑢) + 1, deg+(𝑣) = deg−(𝑣) − 1；
2 𝑉 − {𝑢, 𝑣} 中所有结点的出度等于入度．

• Fleury 算法可以在多项式时间内找出欧拉图 𝐺 中的一条欧拉回路．

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为连通的欧拉图，
Step 1 任取 𝑣0 ∈ 𝑉 ，令 𝑃0 = 𝑣0 ．
Step 2 设 𝑃𝑖 = 𝑣0 𝑒1 𝑣1 𝑒2 … 𝑒𝑖 𝑣𝑖 已经行遍，从 𝐸 − {𝑒1 , 𝑒2 , … , 𝑒𝑖 } 中选取边 𝑒𝑖+1 使得
1 𝑒𝑖+1 与 𝑣𝑖 相关联；
2 除非没有其他选择，𝑒𝑖+1 不应为 𝐸 − {𝑒1 , 𝑒2 , … , 𝑒𝑖 } 中的割边．
Step 3 当 Step 2 不能再执行时，停止．
Fleury 算法终止时得到的即是 𝐺 的欧拉回路．

⭐汉密尔顿图的概念和若干充分条件、必要条件：

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为无向图，
• 经过图 𝐺 的每个结点一次而且仅一次的回路称为哈密尔顿回路，存在哈密尔顿回路的图称为哈密尔顿图 (Hamiltonian graph)．
• 经过图 𝐺 的每个结点一次而且仅一次的通路称为哈密尔顿路，存在哈密尔顿路而无哈密尔顿回路的图称为半哈密尔顿图 (semi-Hamiltonian graph)．

哈密尔顿图和半哈密尔顿图是连通图．(存在每个点都在的路了)

⭐哈密尔顿图的必要条件：

1.如果 𝐺 = ⟨𝑉 , 𝐸⟩ 是哈密尔顿图，则对于任一非空真子集 𝑆 ⊂ 𝑉 ，均有 𝜔(𝐺 − 𝑆) ≤ |𝑆|．

设 𝐶 是 𝐺 中的一条哈密尔顿回路．若 𝑆 = {𝑣}，显然 𝜔(𝐶 − 𝑣) = 1 ≤ |𝑆| = 1．下设 |𝑆| ≥ 2．设 𝑆 中的结点在 𝐶 上分成 𝑟(1 ≤ 𝑟 ≤ |𝑆|) 条互不相邻的路，则 𝜔(𝐶 − 𝑆) = 𝑟 ≤ |𝑆|．注意到 𝐶 − 𝑆 是 𝐺 − 𝑆 的生成子图，所以𝜔(𝐺 − 𝑆) ≤ 𝜔(𝐶 − 𝑆) ≤ |𝑆|.

2.如果 𝐺 = ⟨𝑉 , 𝐸⟩ 是半哈密尔顿图，则对于任一非空真子集 𝑆 ⊂ 𝑉 ，均有 𝜔(𝐺 − 𝑆) ≤ |𝑆| + 1．

设 𝑃 是 𝐺 中一条哈密尔顿路，起点和终点分别为 𝑢 和 𝑣，则 𝐺′ = 𝐺 ∪ (𝑢, 𝑣) 为哈密尔顿图．由上一定理可知，𝜔(𝐺′ − 𝑆) ≤ |𝑆|，因此𝜔(𝐺 − 𝑆) = 𝜔 (𝐺′ − 𝑆 − (𝑢, 𝑣)) ≤ 𝜔 (𝐺′ − 𝑆) + 1 ≤ |𝑆| + 1.

3.⭐设二部图 𝐺 = ⟨𝑉1 , 𝑉2 , 𝐸⟩，2 ≤ |𝑉1 | ≤ |𝑉2 |，则
1 若 𝐺 是哈密尔顿图，则 |𝑉1 | = |𝑉2 |；
2 若 𝐺 是半哈密尔顿图，则 |𝑉1 | = |𝑉2 | 或 |𝑉1 | + 1 = |𝑉2 |；
3 若 |𝑉2| ≥ |𝑉1 | + 2，则 𝐺 不是哈密尔顿图，也不是半哈密尔顿图．

⭐含哈密尔顿路的充分条件:

1.⭐设 𝐺 为 𝑛 阶无向图简单图，若对 𝐺 中任意不相邻的结点 𝑢, 𝑣，均有 deg(𝑢) + deg(𝑣) ≥ 𝑛 − 1，则𝐺 中存在一条哈密尔顿路．

考虑以每天安排一门的原则，在 7 天内安排 7 门课程的考试，使得同一位教师所任的两门课程的考试不排在接连的两天中，试证明如果没有教师担任多于 4 门课程，则符合上述要求的考试安排总是可能的．

设 𝐺 为具有 7 个结点的图，每个结点对应于一门课程，如果两个结点对应的课程是由不同教师担任的，那么这两个结点之间有一条边．因为每个教师所任课程数不超过 4，故每个结点的度数至少是 3，说明任意两个结点的度数之和至少是 6，故 𝐺 总是包含一条哈密顿路，它对应于一个 7 门考试课目的一个适当的安排．

2.⭐设 𝐺 为 𝑛 阶无向图简单图，若对 𝐺 中任意不相邻的结点 𝑢, 𝑣，均有 deg(𝑢) + deg(𝑣) ≥ 𝑛，则 𝐺是哈密尔顿图．

在某次国际会议的预备会议中，共有 15 人参加，他们来自不同的国家．已知他们中任何两个无共同语言的人与其余有共同语言的人数之和大于或等于 15，问能否将这 15 个人排在圆桌旁，使其任何人都能与两边的人交谈．

作无向图 𝐺 = ⟨𝑉 , 𝐸⟩，将 15 人视为 15 个结点 𝑣1 , 𝑣2 , … , 𝑣15 ，任意不同两点 𝑣𝑖 , 𝑣𝑗 之间有边相连，当且仅当 𝑣𝑖 和 𝑣𝑗 有共同语言．由条件可知，任取 𝑣𝑖 , 𝑣𝑗 ∈ 𝑉 , 𝑖 ≠ 𝑗 且 (𝑣𝑖 , 𝑣𝑗 ) ∉ 𝐸，均有deg(𝑣𝑖) + deg(𝑣𝑗 ) ≥ 15．根据定理 𝐺 中存在哈密尔顿回路，则按照此回路中结点顺序安排圆桌座次即可．

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为 𝑛 阶无向图，图 𝐺 的闭包 (closure) 𝐶 (𝐺) 是指通过如下操作所得到的图：反复连接 𝐺 中度数之和大于或等于 𝑛 的不相邻的结点对 𝑢, 𝑣，直至没有这样的结点对为止．• 𝐺 的闭包 𝐶 (𝐺) 是唯一确定．

⭐哈密尔顿图的充要条件：

1.⭐设 𝑢, 𝑣 为 𝑛 阶无向图 𝐺 中两个不相邻的结点，且 deg(𝑢) + deg(𝑣) ≥ 𝑛，则 𝐺 为哈密尔顿图当且仅当 𝐺 ∪ (𝑢, 𝑣) 为哈密顿尔顿图．

2.一个简单图是哈密尔顿图当且仅当它的闭包是哈密尔顿图．

3.若 𝑛(𝑛 ≥ 3) 阶简单图 𝐺 的闭包 𝐶 (𝐺) 是完全图，则 𝐺 是哈密尔顿图．

4.𝑛(𝑛 ≥ 2) 阶竞赛图中一定存在哈密尔顿路．

对图 𝐺 的边 𝑒，赋以一个实数 𝑤(𝑒)，则称 𝑤(𝑒) 为边 𝑒 的权 (wight)．每条边都带权的图称为带权图 (weighted graph)．设 𝐻 是带权图 𝐺 的子图，则 𝐻 的权定义为 𝑊 (𝐻 ) = ∑𝑒∈𝐸(𝐻) 𝑤(𝑒).

第3章：

树的概念和树的性质：

不含圈的无向连通图称为树 (tree)．
• 树中度数为 1 的结点称为树叶 (leaf)．
• 树中度数大于 1 的结点称为内点 (internal vertex)或分枝点 (branch vertex)．
• 称每个连通分支均为树的无向图为森林 (forest)．

由于树无环且无重边（否则有圈），所以树必是简单图．

设 𝐺 = ⟨𝑉 , 𝐸⟩ 是结点数为 𝑛，边数为 𝑚 的连通图，则 𝑚 ≥ 𝑛 − 1．(连通图，每个点至少关联一条边)

⭐树的等价定义

给定无向图 𝐺 = ⟨𝑉 , 𝐸⟩，结点数记为 𝑛，边数记为 𝑚，则下列命题等价：
1 𝐺 是树．
2 𝐺 中无环且任意两个相异结点之间有且仅有一条路．
3 𝐺 中无圈且 𝑚 = 𝑛 − 1．
4 𝐺 连通且 𝑚 = 𝑛 − 1．
5 𝐺 连通且对任意 𝑒 ∈ 𝐸，均有 𝐺 − 𝑒 不连通．
6 𝐺 无圈且对任意 𝑒 ∈ 𝐸(𝐺)，𝐺 ∪ 𝑒 中有且仅有一个包含 𝑒 的圈．

树 𝐺 中的每一条边都是割边．

无向图 𝑇 是森林的充分必要条件是 𝑚 = 𝑛 − 𝜔，其中 𝑚 为 𝑇 的边数，𝑛 为 𝑇 的结点数，𝜔 为 𝑇的连通分支数．

树的性质

⭐非平凡树至少含有两个树叶（1 度结点）．

生成树：

若图 𝐺 = ⟨𝑉 , 𝐸⟩ 的生成子图 𝑇 是树，则称 𝑇 为 𝐺 的生成树 (spanning tree)．
• 𝑇 中的边称为树枝 (branch)；
• 𝐺 中不属于 𝑇 的边称为弦 (chord)；
• 所有弦导出的子图称为 𝑇 的余树 (cotree)，记为 𝑇 一把．

余树不一定是树

设 𝐺 是 𝑛 个结点 𝑚 条边的无向连通图，𝑇 为 𝐺 的生成树，则 𝑇 的余树 中有 𝑚 − 𝑛 + 1 条边．

图 𝐺 连通当且仅当 𝐺 中有生成树．

⭐连通图的任何一条回路与任何一棵生成树的余树至少有一条公共边。(若存在一条回路和一棵生成树的余树没有公共边，则这条回路包含在这个生成树中，则生成树中含圈，矛盾．)

⭐连通图的任何一个边割集和任何一棵生成树至少有一条公共边．（若有一个边割集和一棵生成树没有公共边，那么删去这个边割集后，所得子图必包含该生成树，这意味着删去边割集后仍是连通图，与边割集定义矛盾．）

⭐最小生成树

在一个带权图 𝐺 的所有生成树中，权最小的生成树称为 𝐺 的最小生成树．(最小生成树的权不用乘以层数)

算法思想： 先从图 𝐺 中找出权最小的一条边作为最小生成树的边，然后逐次从剩余边中选边加入最小生成树中，要求每次挑选不与已选边构成圈的边中权最小的一条，直至选出 |𝑉 (𝐺)| − 1 条边为止．(缺点是要判断会不会构成圈)

算法思想： 任取图 𝐺 中一点，先找出与该点关联的权最小的一条边作为最小生成树的边．在算法任一轮循环中，设已经选出的边导出子图为 𝐺′ ，从 𝐺′ 的结点向 𝐺′ 以外结 点的连边为 𝐸 ′，则选择 𝐸′ 中权最小的边向 𝐺′ 中添加，如此反复循环直至选出|𝑉 (𝐺)| − 1 条边为止．(可以用切割法理解，Prim算法的贪心策略是：每次选取连接U和V-U的所有边中的最短边。)

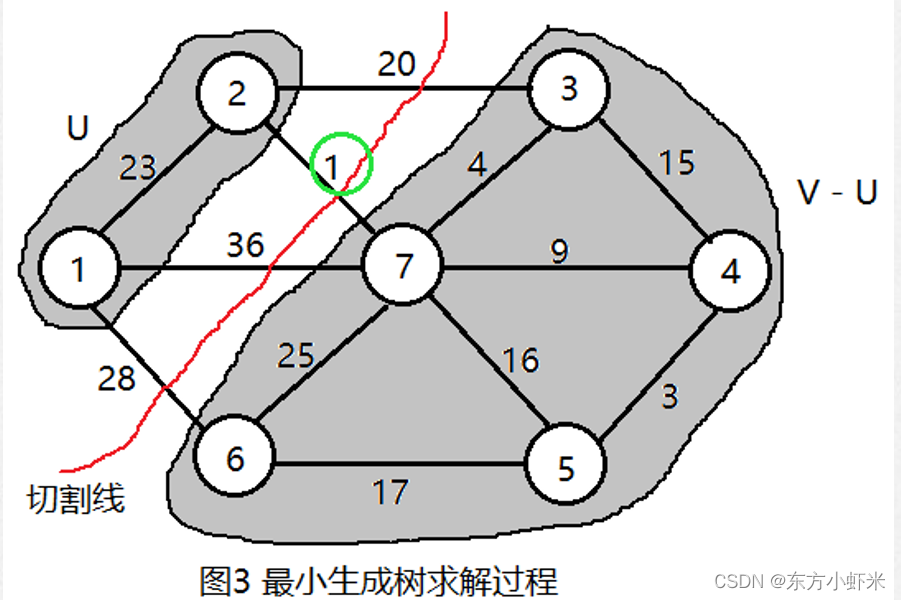
Kruskal 算法和 Prim 算法

• Kruskal 算法在保持无圈的基础上选权最小的边，并不要求每一步保持边生成子图连通．
• Kruskal 算法的添边过程可视为森林合并为树的过程．
• Prim 算法在保持连通性的基础上选权最小的边，并在过程中保持了边生成子图不含圈．
• Prim 算法的添边过程可视为树的生长过程．
• Kruskal 算法又称为避圈法，Prim 算法又称为边割法．

设𝐺为𝑛阶带权图， Kruskal 算法的复杂度为 𝑂(𝑛^2log 𝑛)，Prim 算法的复杂度为 𝑂(𝑛^3 )．

破圈法

算法思想： 设 𝐺 是 𝑛 阶无向连通带权图，若 𝐺 不是树，则 𝐺 中必含有圈．从 𝐺 中的任意圈开始，去掉该圈中权最大的一条边，称为破圈．不断破圈，直至 𝐺 中不含圈，最后剩下的边导出子图，即为 𝐺 中的生成树．

有向树、根树：

一个有向图，若不考虑边的方向，它是一个树，则称该有向图为有向树 (directed tree)．

一棵有向树，若恰有一个结点入度为 0，其余所有结点入度都为 1，则称为根树 (rooted tree)．
• 入度为 0 的结点称为树根 (root)；
• 出度为 0 的结点称为树叶 (leaf)；
• 出度不为 0 的结点称为内点 (internal vertex)或分枝点 (branch vertex)．

出度不为 0 的根点也是分枝点．

在根树中，称从树根到结点 𝑣 的距离为 𝑣 的层次 (level)或高 (height)．称所有结点的高的最大值为根树的高 (height)，即树的高等于从树根出发的最长路的长度．

在根树中，
• 若 𝑣𝑖 到 𝑣𝑗 可达，则称 𝑣𝑖 是 𝑣𝑗 的祖先 (ancestor)，𝑣𝑗 是 𝑣𝑖 的后代 (descendant)；
• 若 ⟨𝑣𝑖, 𝑣𝑗⟩ 是 𝑇 的有向边，则称 𝑣𝑖 是 𝑣𝑗 的父亲 (parent)，𝑣𝑗 是 𝑣𝑖 的儿子 (child)；
• 若 𝑣𝑖 和 𝑣𝑗 是同一结点的儿子，则称 𝑣𝑖 和 𝑣𝑗 是**兄弟 (**siblings)．

根树 𝑇 中，任意结点 𝑣 及其后代的导出子图 𝑇𝑣 称为 𝑇 的以 𝑣 为根的根子树 (rooted subtree)；任意结点 𝑢 的子树 (subtree)是以 𝑢 的某个儿子为根的根子树．

如果对根树中每一层次上结点都标定了从左至右的次序，则称该根树为有序树 (ordered rooted tree)．

一个有向图，如果它的每个连通分支是有向树，则称该有向图为(有向) 森林 ((directed) forest)；在森林中，如果所有树都是有序树且给树指定了次序，则称此森林是有序森林 (ordered forest)．

在根树 𝑇 中，
• 若结点的最大出度为 𝑚，则称 𝑇 为 𝑚 叉树 (𝑚−array tree)；
• 若每个分枝点的出度均为 𝑚，则称 𝑇 为完全 𝑚 叉树 (full 𝑚−array tree)；
• 若完全 𝑚 叉树的所有树叶都在同一层，则称为正则 𝑚 叉树 (regular 𝑚−array tree)．
• 若 𝑇 是 𝑚 叉树且是有序树，则称 𝑇 为𝑚 元有序树 (𝑚-array ordered tree)．

⭐在完全 𝑚 叉树中，若树叶数为 𝑡，分枝点数为 𝑖，则有 (𝑚 − 1)𝑖 + 1 = 𝑡.(因为树叶数为 𝑡，分枝点数为 𝑖，所以该数有 𝑖 + 𝑡 个结点．根据树的等价定义，该树的边数为 𝑖 + 𝑡 − 1．由握手定理可知，所有结点的出度等于边数，根据完全 𝑚 叉树的定义，所以我们有𝑚𝑖 = 𝑖 + 𝑡 − 1，即 (𝑚 − 1)𝑖 + 1 = 𝑡．对于完全 𝑚 叉树，已知结点数 𝑛，分枝点数 𝑖，树叶数 𝑡 中的任意一个，则其它两个可求．)

二叉树 (binary tree)的每个结点 𝑣 至多有两棵子树，分别称为 𝑣 的左子树 (left subtree)和右子树(right subtree)．若结点 𝑣 只有一棵子树，则称它为 𝑣 的左子树或右子树均可．

⭐最优二元树及最佳前缀码:

设二叉树 𝑇 有 𝑡 片树叶，对其树叶分别赋权 𝑤1 , 𝑤2 , … , 𝑤𝑡 ，则称 𝑇 为带权二叉树 (weighted binary tree),它的权 𝑊 (𝑇 ) 定义为𝑊 (𝑇 ) = ∑ 𝑤𝑖 ⋅ 𝐿(𝑤𝑖 ),其中 𝐿(𝑤𝑖) 表示权为 𝑤𝑖 的树叶的层次．

在所有带权 𝑤1 , 𝑤2 , … , 𝑤𝑡 的二叉树中，权 𝑊 (𝑇 ) 最小的树称为最优二叉树 (optimal binary tree)．

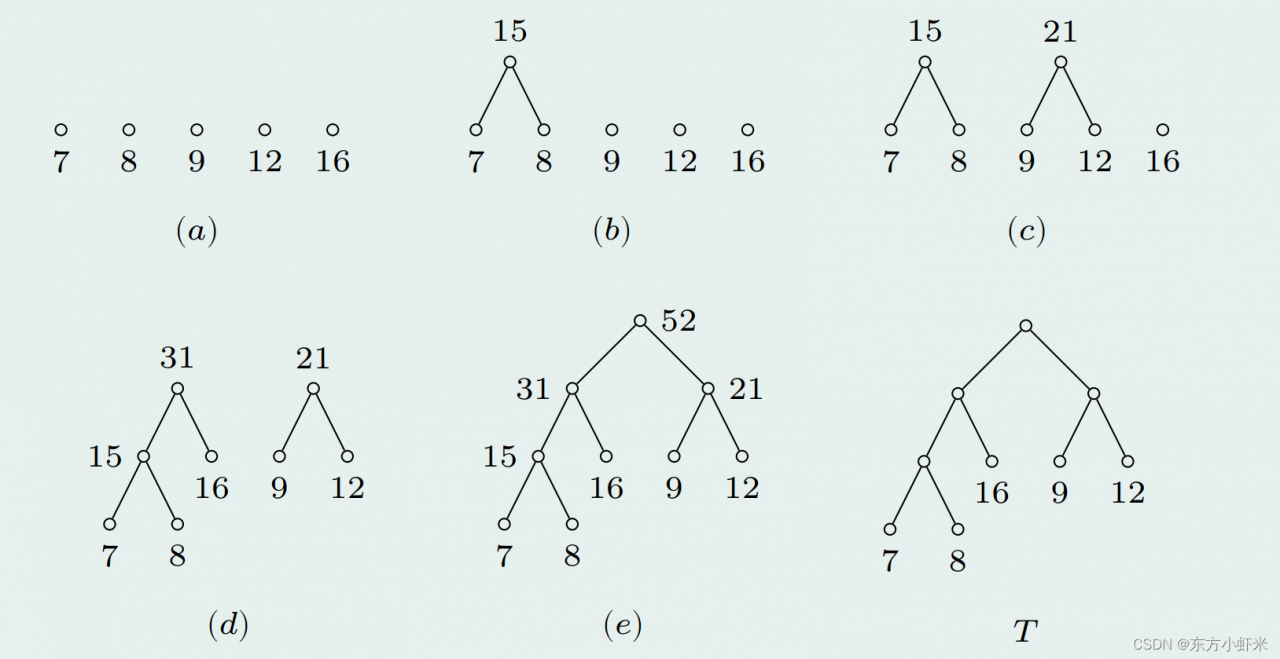
前缀码

• 设 𝑎1𝑎2 ⋯ 𝑎𝑛 是长度为 𝑛 的符号串，称其子串 𝑎1 , 𝑎1 𝑎2 , … , 𝑎1 𝑎2 ⋯ 𝑎𝑛−1 为该符号串的长度为 1, 2, … , 𝑛 − 1 的前缀 (prefix)．
• 设 𝐴 = {𝛽1, 𝛽2, … , 𝛽𝑛} 为一个符号串集合，若 𝐴 中任意两个不同的符号串 𝛽𝑖 和 𝛽𝑗 互不为前缀，则称 𝐴 为一组前缀码 (prefix code)．

• 由 0, 1 组成的字符串集 {00, 001, 0011} 不是前缀码，因为 00 是 001 的前缀．
• 由 0, 1 组成的字符串集 {0, 10, 110, 1110, 1111} 是前缀码．

任意一个二叉树对应一组由 0, 1 组成的前缀码．

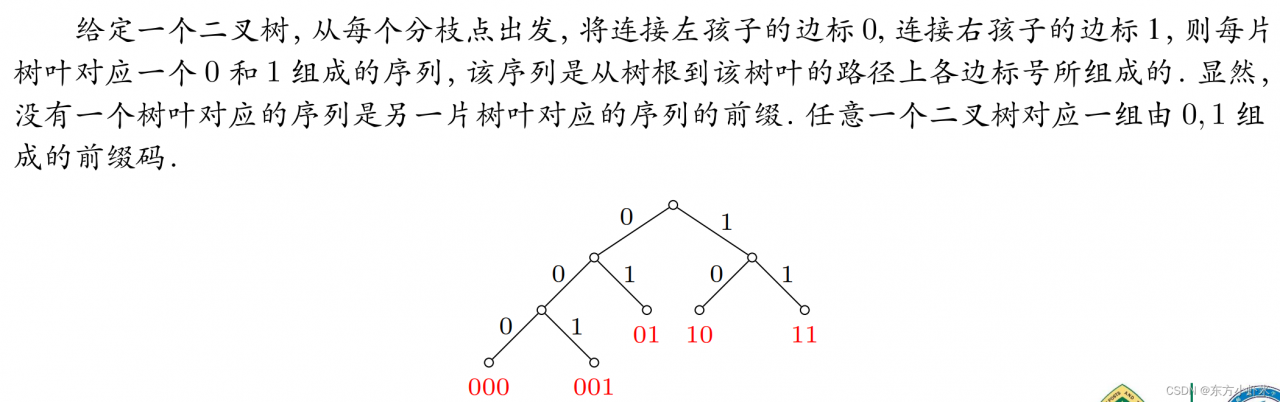
最佳编码

设 26 个英文字母出现的概率分别为 𝑝1 , 𝑝2 , … , 𝑝26 ．最佳编码 (optimal code)是一组码长的数学期望值 ∑p𝑖 𝑙𝑖 最小的前缀码，其中 𝑙𝑖 是第 𝑖 个字母对应的码的长度，对应的图论模型是给定权 𝑝1, 𝑝2 , … , 𝑝26 ，寻找有一个带权 𝑝1 , 𝑝2 , … , 𝑝26 的最优二叉树．

例题:

在某种通信中, 使用八进制数字串．0 − 7 各数字出现的频率如下:
25%; 1 ∶ 20%; 2 ∶ 15%; 3 ∶ 10%; 4 ∶ 10%; 5 ∶ 10%; 6 ∶ 5%; 7 ∶ 5%．
1 求传输这些数字的最佳前缀码;
2 求传输 10𝑛 个按上述比例出现的数字需要多少个八进制数字位？
3 如果用长为 3 的等长码字传输 10𝑛 个按上述比例出现的数字，需要多少个八进制数字位？

1 将频率的百分比作为权，并按从小到大的顺序排列，得到𝑤7 = 5, 𝑤6 = 5, 𝑤5 = 10, 𝑤4 = 10, 𝑤3 = 10, 𝑤2 = 15, 𝑤1 = 20, 𝑤0 = 25.则由 Huffman 算法得到一组最佳前缀码 {0000, 0001, 001, 010, 011, 100, 101, 11}，分别对应 0000 传 7，0001 传 6，001 传 5，010 传 4，011 传 3，100 传 2，101 传 1，11 传 0．

2 由 Huffman 算法得到一组最佳前缀码 {0000, 0001, 001, 010, 011, 100, 101, 11}，分别对应 0000 传 7，0001 传 6，001 传 5，010 传 4，011 传 3，100 传 2，101 传 1，11 传 0．按照给定频传输 100 个数字所用的八进制数字位的个数为100 × (2 × 25% + 3 × 20% + 3 × 15% + 3 × 10% + 3 × 10% + 3 × 10% + 4 × 5% + 4 × 5%) = 285. 所以, 传输 10𝑛 个按上述比例出现的数字需要 2.85 × 10𝑛 个八进制数字位．

3 如果用长为 3 的等长码{000, 001, 010, 011, 100, 101, 110, 111}传输 10𝑛 个按上述频率出现的数字需要 3 × 10𝑛 个八进制数字位．

⭐最短路算法（如Dijkstra算法）：

给定带权图 𝐺 = (𝑉 , 𝐸) 及 𝐺 中两个结点 𝑢, 𝑣，求 𝑢 到 𝑣 的最短路 (the shortest path)，即 𝑢 到 𝑣的具有最小权的路．

Dijkstra 算法

算法思想
• 若 𝑃 = 𝑣0𝑣1 ⋯ 𝑣𝑘−1𝑣𝑘 是 𝑣0 到 𝑣𝑘 的最短路，则 𝑃 ′ = 𝑣0 𝑣1 ⋯ 𝑣𝑘−1 必为 𝑣0 到 𝑣𝑘−1 的最短路．基于此原理，由近及远逐次求出 𝑣0 到其余结点的最短路．

通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。

此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。

初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是”起点s到该顶点的路径”。

然后，从U中找出路径最短的顶点，并将其加入到S中；

接着，更新U中的顶点和顶点对应的路径。 然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。

dijkstra的算法思想是从以上最短距离数组中每次选择一个最近的点，将其作为下一个点，然后重新计算从起始点经过该点到其他所有点的距离，更新最短距离数据。已经选取过的点就是确定了最短路径的点，不再参与下一次计算。

Dijkstra 算法的遗憾
• Dijkstra 算法只能求出了指定结点到其余结点中的最短路，无法一次性得到任意两结点之间的最短路．
• Dijkstra 算法只能作用于所有边都具有非负权的带权图．

Floyd 算法
算法思想： 设 𝐺 = ⟨𝑉 , 𝐸⟩ 为 𝑛 阶带权图，对任意结点 𝑢, 𝑣 ∈ 𝑉 ，设 0 ≤ 𝑘 ≤ 𝑛 − 2，则 𝑢 和 𝑣的距离，即 𝑢 和 𝑣 间的最短路长必定是 𝑢 经过另外 𝑘 个结点到达 𝑣 的最短路长．因此，只需确定 𝑢, 𝑣 间通过 0 个结点，1 个结点，直至 𝑛 − 2 个结点过渡的最短路长的最小值，即能确定 𝑢 到 𝑣 的最短路长．

设 𝐺 为 𝑛 阶带权图，𝐷 = (𝑑𝑖𝑗 )𝑛 为 𝐺 的距离矩阵．
Step 1 输入 𝐷 ∶= 𝐷(0)，置 𝑘 ∶= 1；
Step 2 置 𝑖 ∶= 1；
Step 3 置 𝑗 ∶= 1；
Step 4 𝑑𝑖𝑗 ∶= min {𝑑𝑖𝑗 , 𝑑𝑖𝑘 + 𝑑𝑘𝑗 }；
Step 5 𝑗 ∶= 𝑗 + 1，若 𝑗 ≤ 𝑛，转 Step 4；
Step 6 𝑖 ∶= 𝑖 + 1，若 𝑖 ≤ 𝑛，转 Step 3；
Step 7 𝑘 ∶= 𝑘 + 1，若 𝑘 ≤ 𝑛，转 Step 2；
Step 8 算法终止，𝑑𝑖𝑗 表示 𝑣𝑖 到 𝑣𝑗 的距离．

Floyd–Warshall 算法的算法复杂度为 𝑂(𝑛3 )．

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为带权图，𝑑(𝑢, 𝑣) 为结点 𝑢 到结点 𝑣 的距离，则定义
• 𝐺 中结点 𝑢 的离径 (eccentricity): 𝑒(𝑢) = max𝑣∈𝑉 {𝑑(𝑢, 𝑣)};(u到另一点最远的距离)
• 𝐺 的半径 (radius): rad(𝐺) = min𝑢∈𝑉 {𝑒(𝑢)};
• 𝐺 的直径 (diameter): diam(𝐺) = max𝑢∈𝑉 {𝑒(𝑢)}.
• 𝐺 的中心 (center): 满足 𝑒(𝑢) = rad(𝐺) 的结点 𝑢 称为 𝐺 的中心．

设 𝑃 = 𝑣1𝑣2 ⋯ 𝑣𝑙 𝑣𝑙+1 是树 𝑇 中的一条最长路，则
• 𝑇 的直径为 𝑙；
• 若 𝑙 = 2𝑘 − 1，则 rad(𝑇 ) = 𝑘，𝑇 有两个相邻的中心 𝑣𝑘 , 𝑣𝑘+1 ，且任意长为 𝑙 的路都通过这两
个中心；
• 若 𝑙 = 2𝑘 为偶数，则 rad(𝑇 ) = 𝑘，𝑇 只有一个中心 𝑣𝑘+1 ，且任意长为 𝑙 的路都经过该中心

第5章：

独立集：

设简单无向图 𝐺 = ⟨𝑉 , 𝐸⟩, 𝑆 ⊆ 𝑉 , 𝑆 ≠ ∅.
• 若对任意 𝑢, 𝑣 ∈ 𝑆，有 (𝑢, 𝑣) ∉ 𝐸，则称 𝑆 为 𝐺 的独立集 (independent set)．(s中任二顶点均不相邻)
• 若 𝑆 是独立集，且加入任意结点 𝑢 ∈ 𝑉 − 𝑆 后 𝑆 不再是独立集, 则称 𝑆 为 𝐺 的极大独立集 (maximal independent set)．
• 令 𝛼(𝐺) = max{|𝑆| ∣ 𝑆 是 𝐺 的独立集}，称 𝛼(𝐺) 为 𝐺 的独立数 (independent number)．
• 若 𝑆 是独立集且 |𝑆| = 𝛼(𝐺)，则称 𝑆 为 𝐺 的最大独立集 (maximum independent set)．

• 最大独立集必是一个极大独立集，反之不然．
• 极大独立集不唯一，最大独立集一般也不唯一．

⭐求极大独立集的布尔运算：

给定 𝐺 = ⟨𝑉 , 𝐸⟩，𝑆 ⊆ 𝑉 是 𝐺 的独立集，当且仅当对任意 (𝑣𝑖 , 𝑣𝑗 ) ∈ 𝐸，结点 𝑣𝑖 ∉ 𝑆 或 𝑣𝑗 ∉ 𝑆．(任意一边两端点只有一个在独立集之中)

因 𝐺 的独立集不包含任何一边的两个端点，故表达式 𝜑 在任一独立集上取布尔值 1(𝑇 )；反之，使 𝜑 取值为 1 的结点都是独立集．

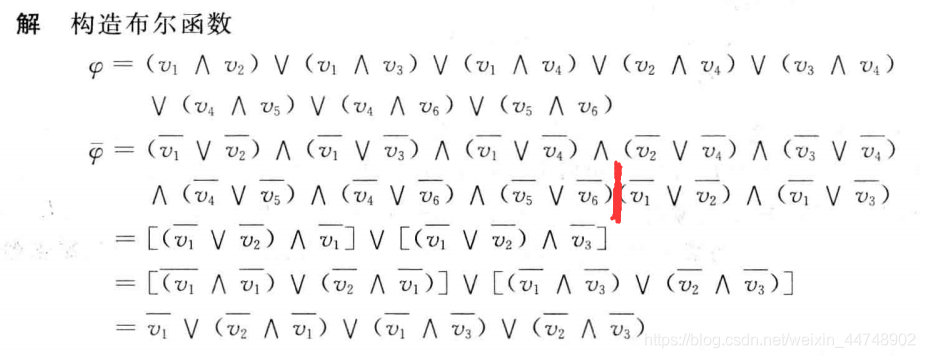
点覆盖：

设简单无向图 𝐺 = ⟨𝑉 , 𝐸⟩, 𝑆 ⊆ 𝑉 , 𝑆 ≠ ∅.
• 若 𝐸 中的每条边都与 𝑆 中的某个结点关联，则称 𝑆 为 𝐺 的点覆盖集 (vertex covering set)，简称点覆盖 (vertex covering)；(任意一条边至少有一个端点在S中)
• 若点覆盖 𝑆 的任意真子集都不是点覆盖，则称 𝑆 为极小点覆盖 (minimal vertex covering)；
• 令 𝛽(𝐺) = min{|𝑆| ∣ 𝑆 是 𝐺 的点覆盖}，则称 𝛽(𝐺) 为 𝐺 的点覆盖数 (vertex covering
number)；
• 若 𝑆 是点覆盖且 |𝑆| = 𝛽(𝐺)，则称 𝑆 为 𝐺 的最小点覆盖 (minimum vertex covering)．

V-S为极大独立集

1 最小点覆盖必是一个极小点覆盖，反之不然．
2 极小点覆盖，最小点覆盖一般不唯一．
3 任意点覆盖，必含有一极小点覆盖．

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为简单无向图，则 𝑆 ⊆ 𝑉 是 𝐺 的点覆盖，当且仅当对任意边 (𝑣𝑖 , 𝑣𝑗 ) ∈ 𝐸(𝐺)，或者 𝑣𝑖 ∈ 𝑆，或者 𝑣𝑗 ∈ 𝑆．

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为简单无向图，对 𝑣 ∈ 𝑉 ，令 𝑁𝐺 (𝑣) = {𝑢 ∣ (𝑣, 𝑢) ∈ 𝐸}，即 𝑁𝐺 (𝑣) 为结点 𝑣 的邻点集，则 𝑆 ⊆ 𝑉 是 𝐺 的点覆盖，当且仅当对任意 𝑣𝑖 ∈ 𝑉 ，或者 𝑣𝑖 ∈ 𝑆，或者 𝑁𝐺 (𝑣𝑖 ) ⊆ 𝑆．(对于任意一点，要么他自己，要么它的邻接点属于S)

⭐点覆盖的布尔计算：

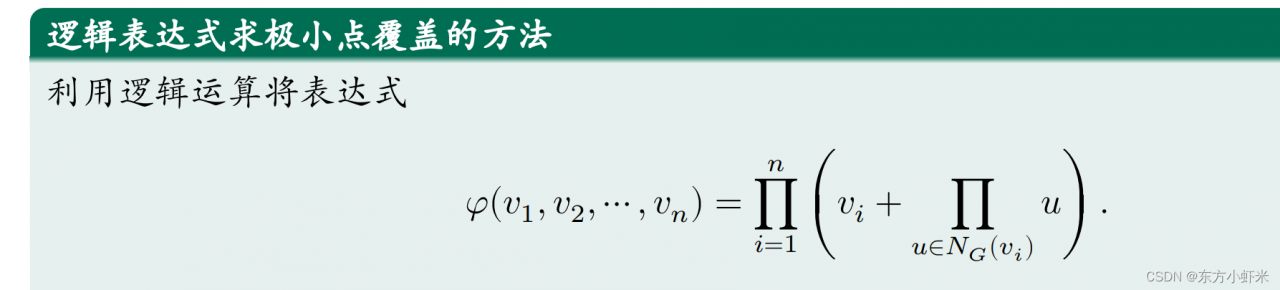
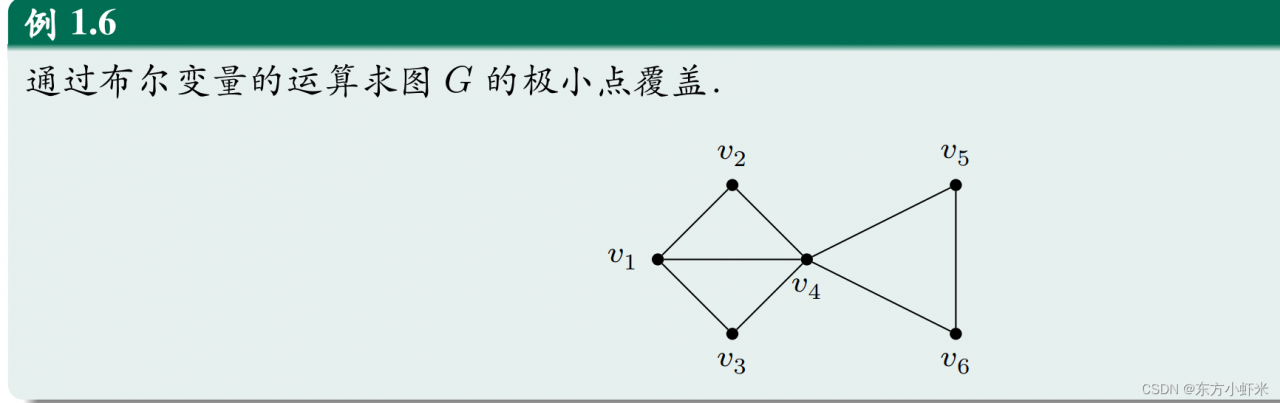
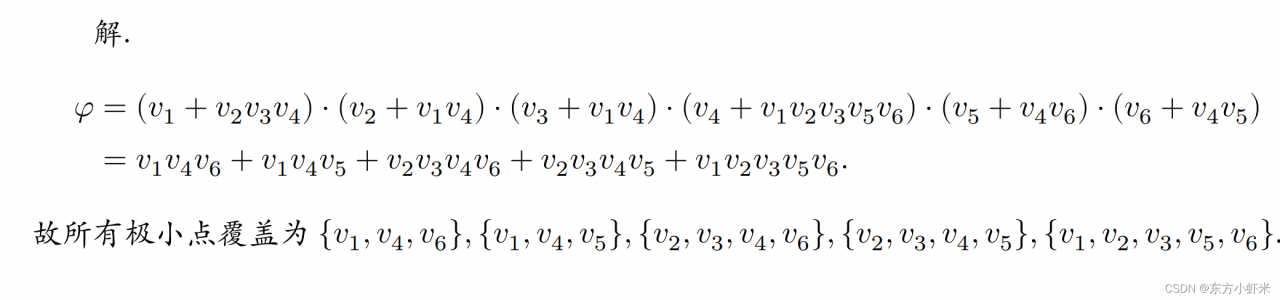
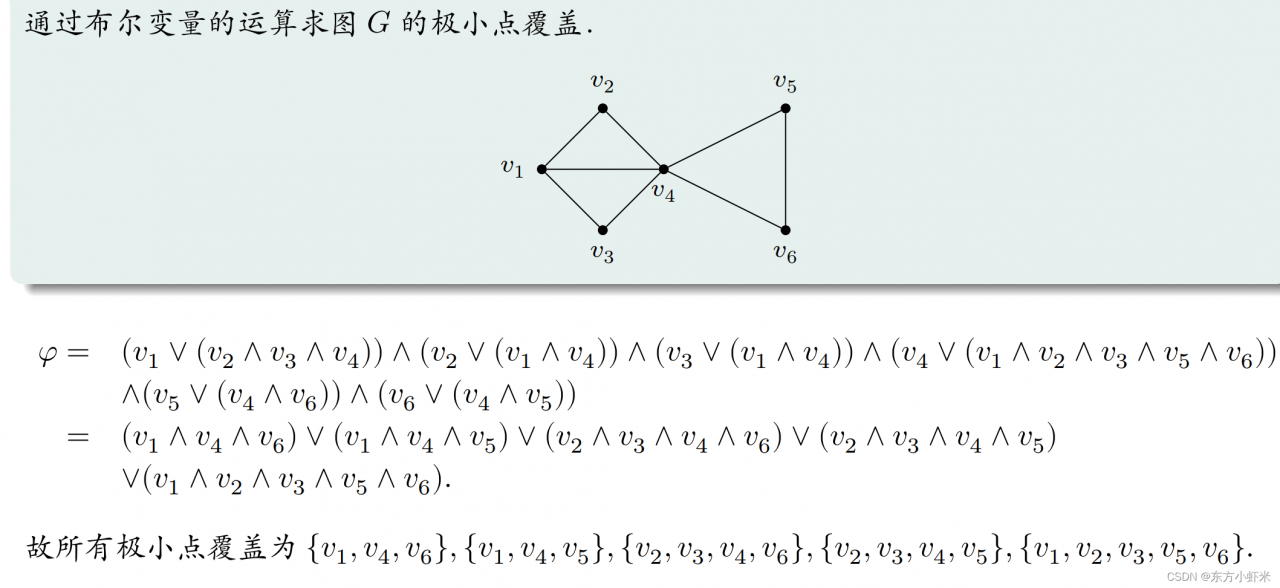
设 𝐺 = ⟨𝑉 , 𝐸⟩ 是简单无向图，𝑆 ⊆ 𝑉 且 𝑆 ≠ ∅，则 𝑆是独立集当且仅当 𝑉 − 𝑆 是 𝐺的点覆盖．(点覆盖比较好求 一般先求点覆盖，再得出独立集)

结点集 𝑆 是图 𝐺 = ⟨𝑉 , 𝐸⟩ 的极大独立集当且仅当 𝑉 − 𝑆 是极小点覆盖．

图 𝐺 = ⟨𝑉 , 𝐸⟩ 的点覆盖数与独立数之和为图 𝐺 的结点数，即 𝛼(𝐺) + 𝛽(𝐺) = |𝑉 |.

边覆盖的定义

设简单无向图 𝐺 = ⟨𝑉 , 𝐸⟩, 𝐿 ⊆ 𝐸, 𝐿 ≠ ∅.
• 若 𝐺 中的每个结点都与 𝐿 中的某条边关联，则称 𝐿 为 𝐺 的边覆盖集 (edge covering set)， 简称边覆盖 (edge covering)；(边集关联的点是所有点)
• 若边覆盖 𝐿 的任意真子集都不是边覆盖，则称 𝐿 为极小边覆盖 (minimal edge covering)；
• 令 𝜃(𝐺) = min{|𝐿| ∣ 𝐿 是 𝐺 的边覆盖}，则称 𝜃(𝐺) 为 𝐺 的边覆盖数 (edge covering number)；
• 若 𝐿 是边覆盖且 |𝐿| = 𝜃(𝐺)，则称 𝐿 为 𝐺 的最小边覆盖 (minimum edge covering)．

支配集:

设简单无向图 𝐺 = ⟨𝑉 , 𝐸⟩, 𝑆 ⊆ 𝑉 , 𝑆 ≠ ∅.
• 若对任意 𝑥 ∈ 𝑉 − 𝑆，有 𝑆 ∩ 𝑁𝐺 (𝑥) ≠ ∅（𝑁𝐺 (x) 为结点 x 的邻点集），则称 𝑆 为 𝐺 的支配集 (domination set)．(对于任一点，要么 u∈S 要么 u 与S 中某顶点相邻)
• 若 𝑆 是支配集，且 𝑆 的任何真子集都不是支配集，则称 𝑆 为 𝐺 的极小支配集 (minimal domination set)．
• 令 𝛾(𝐺) = min{|𝑆| ∣ 𝑆 是 𝐺 的支配集}，称 𝛾(𝐺) 为 𝐺 的支配数 (domination number)．
• 若 𝑆 是支配集且 |𝑆| = 𝛾(𝐺)，则称 𝑆 为 𝐺 的最小支配集 (minimum domination set)．

1 一个图若含孤立结点，则孤立结点必在支配集里．
2 最小支配集必是一个极小支配集，反之不然．
3 任一支配集必含有一个极小支配集．
4 极小支配集不唯一，最小支配集一般也不唯一
5 对二部图 𝐺(𝑋, 𝑌 ) 而言，𝑋 和 𝑌 都是支配集．

⭐求极小支配集的布尔运算：

给定 𝐺 = ⟨𝑉 , 𝐸⟩，𝑆 ⊆ 𝑉 是 𝐺 的支配集，当且仅当对任意 𝑣𝑖 ∈ 𝑉 (𝐺)，或者 𝑣𝑖 ∈ 𝑆，或者 𝑁𝐺(𝑣𝑖) ∩ 𝑆 ≠ ∅.

图 𝐺 = ⟨𝑉 , 𝐸⟩ 的支配集 𝑆 是极小支配集当且仅当 𝑆 中的每个结点 𝑥 满足如下条件之一:
1 存在 𝑦 ∈ 𝑉 − 𝑆 使得 𝑁 (𝑦) ∩ 𝑆 = {𝑥}；
2 𝑁 (𝑥) ∩ 𝑆 = ∅.

若图 𝐺 = ⟨𝑉 , 𝐸⟩ 中无孤立点，且 𝑆 是 𝐺 的极小支配集，则 𝑉 − 𝑆 也是 𝐺 的支配集

若图 𝐺 = ⟨𝑉 , 𝐸⟩ 中无孤立点，则对 𝐺 中任意极小支配集 𝑆1 ，总存在极小支配集 𝑆2 ，使得𝑆1 ∩ 𝑆2 = ∅.

若图 𝐺 = ⟨𝑉 , 𝐸⟩ 中无孤立点，则在 𝐺 中必存在最小支配集 𝑆，使得对任意 𝑥 ∈ 𝑆，总存在𝑦 ∈ 𝑉 − 𝑆，使得 𝑁 (𝑦) ∩ 𝑆 = {𝑥}．

图 𝐺 的结点集 𝑆 是一个独立支配集当且仅当 𝑆 是一个极大独立集.

图 𝐺 的每个极大独立集是一个极小支配集.

对于任何图 𝐺，其独立数大于等于支配数，即 𝛼(𝐺) ≥ 𝛾(𝐺)．

𝛼(𝐺) ≥ 𝛾(𝐺) 中的等号未必总成立，即最大独立集必是极小支配集，但未必是最小支配集．

匹配：

设非空无环图 𝐺 = ⟨𝑉 , 𝐸⟩，𝑀 ⊆ 𝐸(𝐺), 𝑀 ≠ ∅.
• 若 𝑀 中任意两条边在 𝐺 中都不相邻，则称 𝑀 为 𝐺 的匹配 (matching)．
• 若 𝑀 是匹配，且增加任何边后 𝑀 都不是匹配，则称 𝑀 为 𝐺 的极大匹配 (maximal matching)．
• 令 𝜂(𝐺) = max{|𝑀 | ∣ 𝑀 是 𝐺 的匹配}，称 𝜂(𝐺) 为 𝐺 的匹配数 ( matching number)．
• 若 𝑀 是匹配且 |𝑀 | = 𝜂(𝐺)，则称 𝑀 为 𝐺 的最大匹配 (maximum matching)．

设 𝑀 是图 𝐺 的匹配，称 𝐺 中与 𝑀 中的边关联的结点称为 𝑀 的饱和点 (saturated vertex)．若图 𝐺 的结点都是匹配 𝑀 的饱和点，则称 𝑀 为 𝐺 的完美匹配 (perfect matching)．

设 𝑀 是图 𝐺 的匹配，𝑃 是 𝐺 的一条路，且 𝑀 的边和 𝐸(𝐺) − 𝑀 的边在路 𝑃 中交替出现，则称 𝑃 为𝑴 交错路 (alternating path)．若 𝑀 交错路 𝑃 的两个端点为 𝑀 的非饱和点，则称 𝑃 为𝑴 增广路 (augmenting path)．

设无向图 𝐺 = ⟨𝑉 , 𝐸⟩，𝑀 为 𝐺 的最大匹配当且仅当 𝐺 中不含 𝑀 增广路．

求最大匹配的可行方法

给定一个初始匹配 𝑀 = ∅，
• 若 𝐺 存在不饱和点 𝑣，则可通过一定的方法搜索以 𝑣 为端点的 𝑀 增广路，从而扩展 𝑀 ．
• 若 𝐺 中无不饱和点，则 𝑀 是最大匹配．

图 𝐺 的含有奇数个结点的连通分支称为 𝐺 的奇分支 (odd component)．𝐺 的奇分支的个数用 𝜔𝑜(𝐺) 表示．

图 𝐺 有完美匹配的充要条件是对任意真子集 𝑆 ⊂ 𝑉 ，均有 𝜔𝑜 (𝐺 − 𝑆) ≤ |𝑆|．

设 𝐺 = ⟨𝑉 , 𝐸⟩ 为 3− 正则图，且不含割边，则 𝐺 中必存在完美匹配．

设 𝑀 是 𝐺 的一个匹配，𝑆 是 𝐺 的一个点覆盖，且 |𝑀 | = |𝑆|，则 𝑀 是 𝐺 的一个最大匹配，𝑆 是 𝐺 的一个最小点覆盖．

设 𝑛 阶图 𝐺 = ⟨𝑉 , 𝐸⟩ 中无孤立点，则 𝜂(𝐺) + 𝜃(𝐺) (最小边覆盖) = 𝑛．

⭐二部图的匹配：

Hall 定理

设 𝐺 = ⟨𝑋, 𝑌 , 𝐸⟩ 为二部图, 则 𝐺 有饱和 𝑋的匹配当且仅当对任意 𝑆 ⊆ 𝑋，都有 |𝑁 (𝑆)| ≥ |𝑆|．

设 𝐺 = ⟨𝑋, 𝑌 , 𝐸⟩ 为二部图，𝐺 中完美匹配当且仅当 |𝑉1 | = |𝑉2 | 且对任意 𝑆 ⊆ 𝑋(或 𝑌 )，都有|𝑁 (𝑆)| ≥ |𝑆|．

设 𝑘 > 0，𝐺 是 𝑘− 正则二部图，则 𝐺 有完美匹配．

设 𝐺 = ⟨𝑋, 𝑌 , 𝐸⟩ 为简单二部图，且 |𝑋| = |𝑌 | = 𝑛，若 𝛿(𝐺) ≥ 𝑛/2 ，则 𝐺 有完美匹配．

设 𝐺 = ⟨𝑋, 𝑌 , 𝐸⟩ 为连通二部图，则 𝐺 的每条边都含在一个完美匹配中的充分必要条件是 |𝑋| = |𝑌 |，且对 𝑋 中的每一个非空真子集 𝑆，均有|𝑁 (𝑆)| ≥ |𝑆| + 1.

最大匹配问题

指派问题 (assignment problem)
欲安排 𝑛 个人员 𝑥1 , 𝑥2 , … , 𝑥𝑛 从事 𝑛 项工作 𝑦1 , 𝑦2 , … , 𝑦𝑛 ．已知每个人能胜任其中一项或几项 工作．试问：能否给每个人 𝑥𝑖 分配一项他所胜任的工作 𝑦𝑗 ？若能，如何求出这种安排．

图论模型
构造二部图 𝐺 = ⟨𝑋, 𝑌 , 𝐸⟩，其中 𝑋 = {𝑥1 , 𝑥2 , … , 𝑥𝑛 }，𝑌 = {𝑦1 , 𝑦2 , … , 𝑦𝑛 }，(𝑥𝑖 , 𝑦𝑗 ) ∈ 𝐸 当且仅当 𝑥𝑖 胜任工作 𝑦𝑗 ．

理论基础

设无向图 𝐺 = ⟨𝑉 , 𝐸⟩，𝑀 为 𝐺 的最大匹配当且仅当 𝐺 中不含 𝑀 增广路．

设 𝐺 = ⟨𝑋, 𝑌 , 𝐸⟩ 为二部图, 则 𝐺 有饱和 𝑋的匹配当且仅当对任意 𝑆 ⊆ 𝑋，都有 |𝑁 (𝑆)| ≥ |𝑆|．

匈牙利算法

设 𝐺 = ⟨𝑋, 𝑌 , 𝐸⟩ 为二部图，𝑀 为 𝐺 的任意匹配．
1 若 𝑀 饱和 𝑋，则 𝑀 为最大匹配，算法结束．
2 若 𝑀 不能饱和 𝑋, 则在 𝑋 中选择一个 𝑀 非饱和点 𝑥,
• 若 𝐺 中存在以 𝑥 为起点的 𝑀 增广路 𝑃 ，则 𝑀 ′ = 𝑀 ⊕ 𝑃 就是比 𝑀 更大的匹配，以 𝑀 ′ 代替 𝑀 ，并重复这个过程．
• 若 𝐺 中不存在以 𝑥 为起点的 𝑀 增广路，则 𝐺 中不存在饱和 𝑋 的匹配．称 𝑥 为检验过的 𝑀 非 饱和点．对 𝑋 中其余未检验过的 𝑀 非饱和点重复该过程，直到 𝑋 中的所有 𝑀 非饱和点全部 检验过为止．当整个过程结束时，由于 𝐺 中不存在 𝑀 增广路，从而 𝑀 为 𝐺 的最大匹配．

最优匹配问题

图论模型
给定带权完全二部图 𝐾𝑛,𝑛 = ⟨𝑋, 𝑌 , 𝐸⟩，其中 𝑋 = {𝑥1 , 𝑥2 , … , 𝑥𝑛 }，𝑌 = {𝑦1 , 𝑦2 , … , 𝑦𝑛 }，边(𝑥𝑖, 𝑦𝑗) 带非负权 𝑤𝑖𝑗（𝑤𝑖𝑗 = 0 表示 𝑥𝑖 不能胜任工作 𝑦𝑗 ）．

给定带权二部图 𝐺 = ⟨𝑋, 𝑌 , 𝐸⟩ 及结点集 𝑋 ∪ 𝑌 上的一个标号 𝑙，令 𝑙(𝑣) 表示结点 𝑣 的标号．若对任意 (𝑥, 𝑦) ∈ 𝐸，均有 𝑙(𝑥) + 𝑙(𝑦) ≥ 𝑤(𝑥, 𝑦)，则称这个标号为 𝐺 的一个可行结点标号 (feasible vertex labeling)．(其实就是取权值最大的一组x，y。)

根据该网址的例子很好理解https://www.cnblogs.com/wenruo/p/5264235.html

第 6 章:

平面图:

若图 𝐺 能画在曲面 𝑆 上，使得任意两边互不交叉，则称 𝐺 可嵌入曲面𝑆．若图 𝐺 可嵌入平面，则称 𝐺 是可平面图 (planar graph)，否则称为不可平面图 (nonplanar graph)．

可平面图 𝐺 在平面上画出的无交叉边的图示称为 𝐺 的平面嵌入 (planar embedding)．可平面图的任何一个平面嵌入都称为一个平面图 (plane graph)．

将一个可平面图 𝐺 嵌入平面，它平面嵌入不是唯一的.

设 𝐺 是一个的平面图,
• 𝐺 的边将平面划分成若干个区域 (region)；每个区域称为 𝐺 的一个面 (face)；
• 面积有限的面称为有界面 (bounded face)或内部面 (interior face)；
• 面积无限的面称为无界面 (unbounded face)或外部面 (exterior face)；
• 包围一个面的所有边称为该面的边界 (boundary)；
• 面 𝑓 的边界上的边数（割边按两次计）称为该面的度数 (degree of face)，记作 deg(𝑓 )．

平面图 𝐺 中所有面的度数之和等于 𝐺 的边数的两倍

同一个可平面图 𝐺 的平面嵌入中，外部面的度数可以不同

设 𝐺 是简单的可平面图，若对 𝐺 中任意不相邻结点 𝑢 和 𝑣，有 𝐺 + (𝑢, 𝑣) 为不可平面图，则称 𝐺 是极大可平面图 (maximal planar graph)．极大可平面图的任何平面嵌入都称为极大平面图 (maximal plane graph)．

• 𝐾1, 𝐾2, 𝐾3, 𝐾4, 𝐾5 − 𝑒 均为极大可平面图．
• 极大平面图必是连通图．
• 当图的阶数 𝑛 ≥ 3 时，有割点或者桥的平面图不是极大平面图．

设 𝐺 为 𝑛(𝑛 ≥ 3) 阶简单连通平面图，𝐺为极大平面图当且仅当 𝐺的每个面的度数为 3．

如果在不可平面图 𝐺 中任意去掉一条边，所得到的图为可平面图，则称 𝐺 为极小不可平面图 (minimal nonplanar graph)．

⭐欧拉公式:

设 𝐺 是连通的平面图，𝑛, 𝑚, 𝑟 分别是其结点数、边数、面数，则 𝑛 − 𝑚 + 𝑟 = 2．

设 𝐺 是平面图，𝑛, 𝑚, 𝑟, 𝜔 分别是其结点数、边数、面数、连通分支数，则 𝑛 − 𝑚 + 𝑟 = 𝜔 + 1．

设 𝐺 是连通的平面图，𝑛, 𝑚 分别是其结点数和边数，若 𝐺 中各面的度数至少为 𝑙(𝑙 ≥ 3)，则𝑚≤(𝑙/(𝑙 − 2)) (𝑛 − 2).

设 𝐺 是平面图，𝑛, 𝑚, 𝜔 分别是其结点数、边数、连通分支数，若 𝐺 中各面的度数至少为 𝑙(𝑙 ≥ 3)，则𝑚≤(𝑙/(𝑙 − 2)) (𝑛 − 𝜔 − 1).

设 𝐺 是简单平面图，𝑛, 𝑚 分别是其结点数和边数，且 𝑛 ≥ 3，则 𝑚 ≤ 3𝑛 − 6．

设 𝐺 是连通简单平面图，𝑛, 𝑚 分别是其结点数和边数，其中 𝑛 ≥ 3，且 𝐺 中无 3 长圈，则𝑚 ≤ 2𝑛 − 4．

设 𝐺 是任意 𝑛(𝑛 ≥ 3) 阶平面简单图，则 𝛿(𝐺) ≤ 5．

极大平面图的判定

设 𝐺 为连通简单平面图，𝑛, 𝑚, 𝑟 分别是其结点数、边数、面数，且 𝑛 ≥ 3，则下列命题等价：
1 𝐺 是极大平面图．
2 𝐺 中每个面的度数都是 3．
3 3𝑟 = 2𝑚．
4 𝑚 = 3𝑛 − 6．

设 𝑒 = (𝑢, 𝑣) 是图 𝐺 的一条边，在边 𝑒 上加入一个新的结点 𝑤, 将其分为两条新边 (𝑢, 𝑤) 和 (𝑤, 𝑣)，而 𝑤 成为新图的 2 度结点，这个过程称为对边 𝑒 的剖分 (edge subdivision of 𝑒)；对图 𝐺 的边进行一系列剖分后所得之图称为图 𝐺 的剖分图 (subdivision)．

规定图 𝐺 为自身的一个剖分图．

设 𝑒 是图 𝐺 的一条边，从 𝐺 中删去 𝑒 并将 𝑒 的两个端点粘合在一起，删去由此得到的环和重边，这个过程称为边 𝑒 的收缩 (edge contraction of 𝑒)；若图 𝐺1 可通过一系列对边的收缩得到与 𝐺2 同构的图，则称 𝐺1 可收缩到 𝐺2 ．

规定图 𝐺 可收缩到自身．

设 𝑣 是图 𝐺 的一个 2 度结点，将 𝑣，以及与 𝑣 关联的边 (𝑢, 𝑣) 和 (𝑣, 𝑤) 删去，并用新边 (𝑢, 𝑤) 替换，这个过程称为图 𝐺 的2 度结点内收缩．

图 𝐺 为可平面图，当且仅当 𝐺 中即不含 𝐾5 的剖分图，也不含 𝐾3,3 的剖分图．

图 𝐺 是可平面图，当且仅当 𝐺 中既无可收缩为 𝐾5 的子图，也无可收缩到 𝐾3,3 的子图．

图的预处理
• 判断一个图是否是可平面图时，可以对图做一些预处理，使图得到简化．
1 若图 𝐺 非连通，则分别检测每一个连通分支．当且仅当所有的连通分支都是可平面图时，𝐺 是可平面图．
2 若 𝐺 中存在割点 𝑣，可将图 𝐺 从 𝑣 处分离，形成若干个不含割点的连通子图．

3 删去图 𝐺 中的环和重边，环和重边不影响图的可平面性．
4 将图 𝐺 进行 2 度结点内收缩．图 𝐺 是可平面图当且仅当经过 2 度结点内收缩后的新图是可平面图．重复 ❸ ❹ 直至无法进行为止．在所得简单图中做如下判断．
5 若边数 𝑚 < 9，或结点数 𝑛 < 5，则图 𝐺 是可平面图．
6 若边数 𝑚 和结点数 𝑛 满足 𝑚 > 3𝑛 − 6，或最小度 𝛿 > 5，则图 𝐺 是不可平面图．
7 若不满足 ❺ 和 ❻ ，图 𝐺 的平面性不能确定，需要进行进一步检测．

对偶图：

设 𝐺 是无孤立结点的平面图，且 𝐺 有 𝑟 个面 𝑅1 , 𝑅2 , ⋯ 𝑅𝑟 ．按下列过程构造图 𝐺∗ ：
1 在 𝐺 的每个面内设置一个结点 𝑣𝑖 (1 ≤ 𝑖 ≤ 𝑟)．
2 过 𝑅𝑖 与 𝑅𝑗 的每一条公共边 𝑒𝑘 作一条且仅作一条边 (𝑣𝑖 , 𝑣𝑗 ) 与 𝑒𝑘 相交．
3 仅当 𝑒𝑘 只是 𝑅𝑖 的边界时，在 𝑣𝑖 上作一环边与 𝑒𝑘 相交．
称图 𝐺∗ 称为图 𝐺 的对偶图 (dual graph)．若 𝐺∗ 与 𝐺 同构，称 𝐺 是自对偶图 (self-dual graph)．

对偶图的性质
不含孤立结点的平面图 𝐺 的对偶图 𝐺∗ 有如下结论：
• 𝐺∗ 是平面图，而且是平面嵌入；
• 𝐺∗ 是连通图；
• 若边 𝑒 为 𝐺 中的环，则 𝐺∗ 与 𝑒 对应的边 𝑒∗ 为桥；若 𝑒 为桥，则 𝐺∗ 中与 𝑒 对应的边 𝑒∗ 为环；
• 在多数情况下，𝐺∗ 含有平行边；
• 同构的平面图的对偶图不一定同构．

设 𝑛, 𝑚, 𝑟 分别为平面图 𝐺 的结点数，边数及面数，𝑛∗ , 𝑚∗ , 𝑟∗ 分别为 𝐺 的对偶图 𝐺∗ 的结点数，
边数及面数，则：
1 𝑛∗=𝑟,𝑚∗=𝑚;
2 𝑟∗ = 𝑛 − 𝜔 + 1，其中 𝜔 为 𝐺 的连通分支数；
3 设 𝐺∗ 的结点 𝑣𝑖∗ 在 𝐺 的面 𝑅𝑖 中，则 𝑣𝑖∗ 的度数等于 𝑅𝑖 的度数, 即 deg𝐺∗ (𝑣𝑖∗ ) = deg𝐺 (𝑅𝑖 )．

图的点着色:

设 𝐺 是无环边的图．
• 对图 𝐺 的每个结点指定一种颜色，使得相邻的两个结点被指定为不同的颜色，称为对图 𝐺 的点着色 (vertex coloring)，或简称着色 (coloring)．
• 若对图 𝐺 可用 𝑘 种颜色着色，则称 𝐺 为 𝑘 点可着色 (vertex 𝑘−colorable)，或简称 𝑘 可着色 (𝑘−colorable)．
• 若图 𝐺 是 𝑘 可着色，但非 𝑘 − 1 可着色的，则称图的点色数 (vertex chromatic number)或色数 (chromatic number)为 𝑘，记为 𝜒(𝐺) = 𝑘，即 𝜒(𝐺) = min{𝑘 ∣ 𝐺 是 𝑘 可着色的}．

• 图 𝐺 = ⟨𝑉 , 𝐸⟩ 一定是 |𝑉 | 可着色的．
• 若图 𝐺 是 𝑘 可着色的，则对任何整数 𝑚 ≥ 𝑘，图 𝐺 亦是 𝑚 可着色的．
• 对图 𝐺 的任何子图 𝐻 ⊆ 𝐺，均有 𝜒(𝐻 ) ≤ 𝜒(𝐺)．

设 𝐺 是无环边的图．
• 对图 𝐺 的每条边指定一种颜色，使得相邻的两条边被指定为不同的颜色，称为对图 𝐺 的边着色 (edge coloring)．
• 若对图 𝐺 可用 𝑘 种颜色边着色，则称 𝐺 为 𝑘 边可着色 (vertex 𝑘-colorable)．
• 若图 𝐺 是 𝑘 边可着色，但非 𝑘 − 1 边可着色的，则称图的边色数 (vertex chromatic number)为 𝑘，记为 𝜒′(𝐺) = 𝑘，即 𝜒′ (𝐺) = min{𝑘 ∣ 𝐺 是 𝑘 边可着色的}．

试确定 𝑛 长圈 𝐶𝑛 的色数．
若 𝑛 = 2𝑘 (𝑘 ≥ 0)，则 𝜒(𝐶2𝑘 ) = 2；若 𝑛 = 2𝑘 + 1 (𝑘 ≥ 0)，则 𝜒(𝐶2𝑘+1 ) = 3．

试确定 𝑛 阶完全图 𝐾𝑛 和完全二部图 𝐾𝑚,𝑛 的色数．
由于 𝐾𝑛 中任意两个结点都相邻，而相邻结点必须指定不同颜色，故 𝜒(𝐾𝑛 ) = 𝑛．显然 𝜒(𝐾𝑚,𝑛) = 2，即用一种颜色着色 𝑚 个结点，用另一种颜色着色 𝑛 个结点．

点着色的性质

• 若 𝐺 为 𝑛 (𝑛 ≥ 1) 阶零图，则 𝜒(𝐺) = 1;
• 若 𝐺 为至少含有一条非环边的图，则 𝜒(𝐺) ≥ 2;
• 若 𝐺 是完全图 𝐾𝑛，则 𝜒(𝐺) = 𝑛;
• 若 𝐺 是至少有一条边的二部图，则 𝜒(𝐺) = 2;
• 偶圈的色数为 2，奇圈的色数为 3．

⭐图 𝐺 是 2 可着色的当且仅当 𝐺 中不含奇圈．

设 𝑢, 𝑣 为图 𝐺 中不相邻的两个结点，将 𝑢, 𝑣 收缩成一个结点 𝑤，使得 𝐺 中与 𝑢, 𝑣 关联的一切边 均与 𝑤 关联，并删去平行边和环，这种操作称为 𝑢 和 𝑣 的粘合，粘合后的新图记为 𝐺.(𝑢, 𝑣)．

设 𝑢 和 𝑣 是图 𝐺 中不相邻的两个结点，则𝜒(𝐺) = min{𝜒(𝐺 + (𝑢, 𝑣)), 𝜒(𝐺.(𝑢, 𝑣))}.

五色定理: 简单平面图的色数不超过 5．四色猜想: 简单平面图的色数不超过 4.

顺序着色算法

顺序着色法
设 𝐺 = ⟨𝑉 , 𝐸⟩ 为简单无向图，且 𝑉 = {𝑣1 , 𝑣2 , ⋯ , 𝑣𝑛 }．规定对结点 𝑣𝑖 着色 𝑐，记为 𝜋(𝑣𝑖 ) = 𝑐．
Step 1 置 𝑖 ∶= 1．
Step 2 置 𝑐 ∶= 1．
Step 3 若对任意 𝑢 ∈ 𝑁 (𝑣𝑖 )，均有 𝜋(𝑢) ≠ 𝑐，则令 𝜋(𝑣𝑖 ) = 𝑐，转 Step 5．否则，转 Step 4．
Step 4 置 𝑐 ∶= 𝑐 + 1，转 Step 3．
Step 5 若 𝑖 < 𝑛, 置 𝑖 ∶= 𝑖 + 1，转 Step 2．否则，算法停止．

设 𝐺 是简单连通图，顺序着色法产生 𝐺 的一个 Δ(𝐺) + 1 着色，所以 𝜒(𝐺) ≤ Δ(𝐺) + 1．

⭐图的色多项式：

设图 𝐺 为 𝑛 阶标定图，称图 𝐺 的两个 𝑘 着色是不同的，当且仅当至少存在一个结点 𝑣0 在两个 𝑘 着色中被指定为不同颜色．图 𝐺 的不同 𝑘 着色方式的总数称为图 𝐺 的色多项式 (chromatic polynomial)，记作 𝑓 (𝐺, 𝑘)．

设 𝑢, 𝑣 为图 𝐺 中任意两个不相邻的结点, 则 𝑓 (𝐺, 𝑘) = 𝑓 (𝐺 + (𝑢, 𝑣), 𝑘) + 𝑓 (𝐺.(𝑢, 𝑣), 𝑘).

给定图 𝐺 的一个 𝑘 着色，
• 若 𝑢, 𝑣 被指定不同颜色，则此着色亦是图 𝐺.(𝑢, 𝑣) 的一个 𝑘 着色．
• 若 𝑢, 𝑣 被指定相同颜色，则此着色亦是图 𝐺 + (𝑢, 𝑣) 的一个 𝑘 着色．
因此，
𝑓 (𝐺, 𝑘) = 𝑓 (𝐺 + (𝑢, 𝑣), 𝑘) + 𝑓 (𝐺.(𝑢, 𝑣), 𝑘).

设 𝑒 = (𝑢, 𝑣) 为图 𝐺 中的任意边，则 𝑓 (𝐺, 𝑘) = 𝑓 (𝐺 − 𝑒, 𝑘) − 𝑓 (𝐺\𝑒, 𝑘).

设 𝐺 为连通简单图，则存在完全图 𝐾𝑛1 , 𝐾𝑛2 , … , 𝐾𝑛𝑟 使得𝑓 (𝐺, 𝑘) = 𝑓 (𝐾𝑛1 , 𝑘) + 𝑓 (𝐾𝑛2 , 𝑘) + ⋯ + 𝑓 (𝐾𝑛𝑟 , 𝑘),其中 𝜒(𝐺) = min{𝑛1 , 𝑛2 , … , 𝑛𝑟 }．

设 𝐺 为 𝑛 阶标定图，则色多项式 𝑓 (𝐺, 𝑘) 的首项为 𝑘^𝑛 ，常数项为 0，且系数的符号为正负相间．

否则，转 Step 4．
Step 4 置 𝑐 ∶= 𝑐 + 1，转 Step 3．
Step 5 若 𝑖 < 𝑛, 置 𝑖 ∶= 𝑖 + 1，转 Step 2．否则，算法停止．

设 𝐺 是简单连通图，顺序着色法产生 𝐺 的一个 Δ(𝐺) + 1 着色，所以 𝜒(𝐺) ≤ Δ(𝐺) + 1．

⭐图的色多项式：

设图 𝐺 为 𝑛 阶标定图，称图 𝐺 的两个 𝑘 着色是不同的，当且仅当至少存在一个结点 𝑣0 在两个 𝑘 着色中被指定为不同颜色．图 𝐺 的不同 𝑘 着色方式的总数称为图 𝐺 的色多项式 (chromatic polynomial)，记作 𝑓 (𝐺, 𝑘)．

设 𝑢, 𝑣 为图 𝐺 中任意两个不相邻的结点, 则 𝑓 (𝐺, 𝑘) = 𝑓 (𝐺 + (𝑢, 𝑣), 𝑘) + 𝑓 (𝐺.(𝑢, 𝑣), 𝑘).

给定图 𝐺 的一个 𝑘 着色，
• 若 𝑢, 𝑣 被指定不同颜色，则此着色亦是图 𝐺.(𝑢, 𝑣) 的一个 𝑘 着色．
• 若 𝑢, 𝑣 被指定相同颜色，则此着色亦是图 𝐺 + (𝑢, 𝑣) 的一个 𝑘 着色．
因此，
𝑓 (𝐺, 𝑘) = 𝑓 (𝐺 + (𝑢, 𝑣), 𝑘) + 𝑓 (𝐺.(𝑢, 𝑣), 𝑘).

设 𝑒 = (𝑢, 𝑣) 为图 𝐺 中的任意边，则 𝑓 (𝐺, 𝑘) = 𝑓 (𝐺 − 𝑒, 𝑘) − 𝑓 (𝐺\𝑒, 𝑘).

设 𝐺 为连通简单图，则存在完全图 𝐾𝑛1 , 𝐾𝑛2 , … , 𝐾𝑛𝑟 使得𝑓 (𝐺, 𝑘) = 𝑓 (𝐾𝑛1 , 𝑘) + 𝑓 (𝐾𝑛2 , 𝑘) + ⋯ + 𝑓 (𝐾𝑛𝑟 , 𝑘),其中 𝜒(𝐺) = min{𝑛1 , 𝑛2 , … , 𝑛𝑟 }．

设 𝐺 为 𝑛 阶标定图，则色多项式 𝑓 (𝐺, 𝑘) 的首项为 𝑘^𝑛 ，常数项为 0，且系数的符号为正负相间．
做题方法 左加边，右收缩边,都为完全图时相加(当为减边时，相减，减边后一个点和一个其他图，色多项式为k乘以这个图的多项式)