0.本系列目的
理解
与
运用
LQR
理解
六个问题
解释什么是LQR,并梳理LQR求解过程。
大家可以思考这么几个问题:
- LQR控制的是什么(什么是LQR)?
- LQR的适用场景是(使用条件)?
- LQR的变量是什么,输入是什么,输出是什么?
- LQR是怎么解决这些问题的?
- LQR中有没有为了优化问题设置的假设条件?
- 在实际控制中,怎么改变状态变量的初值,如果我想让LQR控制器控制的某个状态变量存在稳态误差,该怎么设置参数?
- 可能需要一点自控理论知识,不过对聪明人来说,学过矩阵乘法就行^ ^
如果看不懂就看下面的参考文章,
保证好懂
本文部分片段搬运自以下文章,并根据学校课件和个人理解进行修改,侵删!
(个人感觉最好✨→)
线性二次型调节器(LQR)原理详解
https://blog.csdn.net/qq_36133747/article/details/123413115
LQR最优控制方法小结
https://zhuanlan.zhihu.com/p/363033191
RoboMaster平衡步兵机器人控制系统设计
https://zhuanlan.zhihu.com/p/563048952
运用
一阶倒立摆
matlab+simscape multibody实现
-
对
一阶倒立摆
模型进行建模,设计LQR参数 -
在
matlab
上,实现模型的框图设计 -
通过
simscape multibody
将这一过程可视化
见下一期
LQR的理解与运用 第二期——一阶倒立摆在matlab上的LQR实现
简单的轮足模型(二阶倒立摆)
参考
RoboMaster平衡步兵机器人控制系统设计
构造以下模型
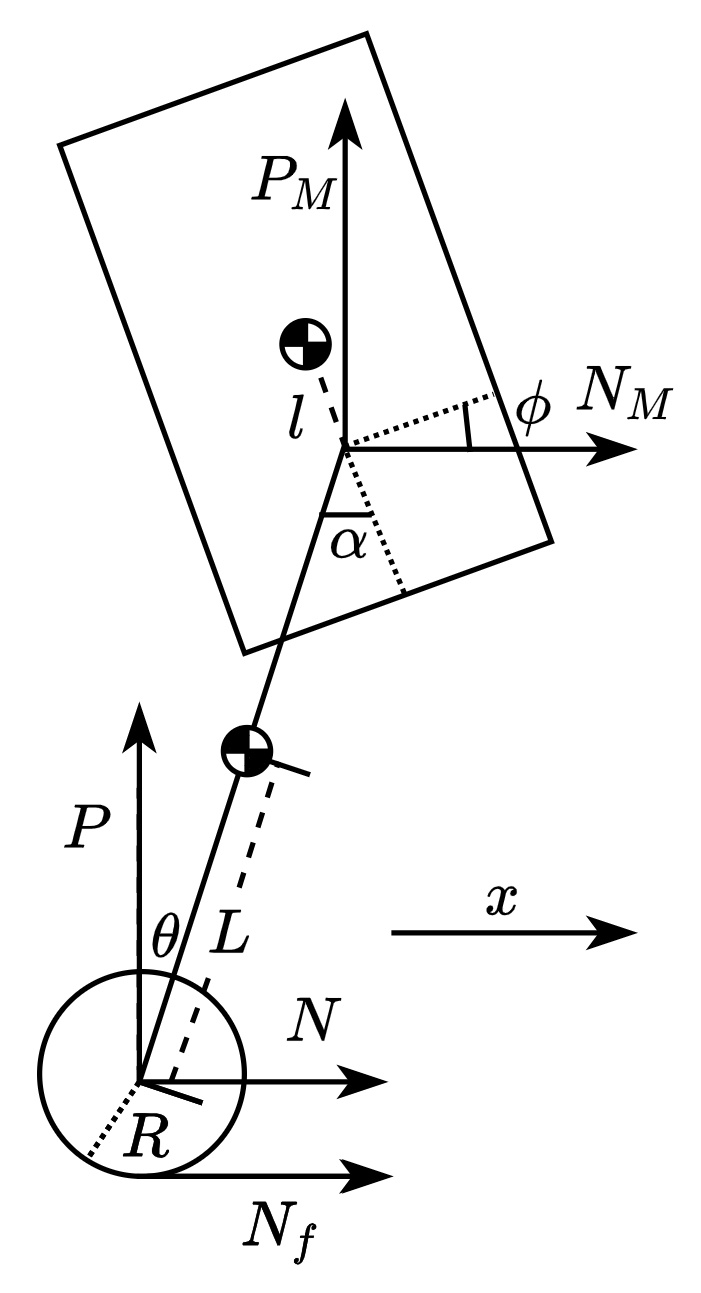
1 理解LQR
写在前面
本文讨论LQR基本原理时,被控对象都是线性定常系统,即系统状态不随时间变化的系统。状态空间表达如下:
x
˙
=
A
x
+
B
u
y
=
C
x
+
D
u
(1)
\begin{array}{l} \dot{x}=A x+B u \\ y=C x+D u \end{array}\tag{1}
x
˙
=
A
x
+
B
u
y
=
C
x
+
D
u
(
1
)
| 符号 | 意义 |
|---|---|
|
A A A |
状态转移矩阵,描述了系统状态的演化规律。 |
|
B B B |
输入矩阵,描述了外部输入对系统状态的影响。 |
|
C C C |
输出矩阵,描述了状态变量如何映射到输出信号。 |
|
D D D |
直接传递矩阵,描述了外部输入直接传递到输出信号的影响。 |
|
x x x |
状态变量,系统的内部状态,可以描述系统的动态特性。 |
|
u u u |
输入变量,系统的外部输入,可以是一个或者多个变量。 |
|
Q Q Q |
控制效果矩阵,表示控制器对状态变量的重视程度。 |
|
R R R |
状态效果矩阵,表示控制器对控制输入的重视程度。 |
Q1:LQR控制的是什么
结论
:LQR控制的是线性时不变系统的
状态变量
x
x
x
的变化。
具体而言,LQR通过对系统状态变量的反馈控制,使系统状态向着期望的状态稳定,并且能够实现一定的性能指标要求,如响应速度、稳态误差等。
我们设定一个线性反馈控制器
u
=
−
K
x
u=-K x
u
=
−
K
x
,用以得到
输入参数
u
{u}
u
与
状态变量
x
{x}
x
的关系(求解矩阵
K
K
K
的方法会在后面提到),此时第一行可以写为
x
˙
=
A
x
−
B
K
x
=
(
A
−
B
K
)
⏟
A
c
l
x
(2)
\dot{x}=A x-B K x=\underbrace{(A-B K)}_{A_{c l}} x\tag{2}
x
˙
=
A
x
−
B
K
x
=
A
c
l
(
A
−
B
K
)
x
(
2
)
让系统稳定的条件是矩阵
A
c
l
A_{cl}
A
c
l
的特征值的实部均为负数(?),我们当然可以
手动选择
几个满足上述条件的特征值,然后反解
K
K
K
,从而得到控制器。
而LQR的出现,就是为了让几个参数的选择更为合理,从而使得控制器
控制效果更好
。其实现方式正是通过设计代价函数
J
J
J
实现的。
本文讨论
无限时间
的LQR问题(有限时间的LQR问题属于状态时变的问题,这里暂时不考虑),无限时间的LQR问题设计的成本代价泛函
J
J
J
为:
J
=
∫
0
∞
(
x
T
Q
x
+
u
T
R
u
)
d
t
,
Q
=
Q
T
,
R
=
R
T
,
Q
≥
0
,
R
>
0
(3)
J=\int_{0}^{\infty}\left(x^{T} Q x+u^{T} R u\right) d t, Q=Q^{T}, R=R^{T}, Q \geq 0, R>0\tag{3}
J
=
∫
0
∞
(
x
T
Q
x
+
u
T
R
u
)
d
t
,
Q
=
Q
T
,
R
=
R
T
,
Q
≥
0
,
R
>
0
(
3
)
一般来说,Q阵和R阵为
对角阵
,分别确定了状态变量
x
x
x
和输入参数
u
u
u
的权重。对角阵上的
值越大
说明我们设计时对于该量的
重视程度越大
,即希望这个量在变化过程中保持较小的值,换种说法就是对于该量的“惩罚”越大。我们的设计目标就是得到一系列的控制序列使代价累积的最小。
代价函数的解释,举例:

图片内容及部分文字来自
线性二次型调节器(LQR)原理详解
因此,问题转变为了选择合适的反馈矩阵
K
K
K
使得代价函数
J
J
J
最小。
(见Q3)
Q2:LQR的适用场景与形式
-
LQR是一个多输入,多输出(MIMO)的
调节器
(仅适用于线性系统);其
目的
是在给定
代价为二次的
代价方程中找出最小代价。 -
在多个输入参数中,可分别设置不同权重。
此外,由于LQR为
状态方程形式
,因此输入参数为
n*1
的形式,而权重矩阵(下文
Q,
R
Q,R
Q
,
R
)往往是
n*n
的对角矩阵,即除了主对角线均为0;故为了表现
加权
、
二次
、
多输入
,代价函数往往为以下形式:(
xx
x
,
uu
u
的位置见上文状态空间表达形式)
J=
x
T
(
t
)
Q
x
(
t
)
+
u
T
(
t
)
R
u
(
t
)
J = x^{T}(t) Q x(t)+u^{T}(t) R u(t)
J
=
x
T
(
t
)
Q
x
(
t
)
+
u
T
(
t
)
R
u
(
t
)
Q3:LQR的变量、输入、输出
-
变量
:状态变量
xx
x
和输入变量
uu
u
,作用在前面表格中已列出。 -
输入
:在LQR设计中,我们需要选择合适的状态反馈矩阵K,使得反馈控制器能够有效地控制系统状态的变化,并实现期望的性能指标。
在状态方程
Q4:LQR的解决思路
接Q1,下一步是选择合适的反馈矩阵
K
K
K
使得代价函数
J
J
J
最小。
根据式
(
3
)
(3)
(
3
)
,我们另定义一个辅助常量矩阵
P
P
P
,
d
d
t
x
T
P
x
=
−
(
x
T
Q
x
+
u
T
R
u
)
(4)
\frac{\mathrm{d}}{\mathrm{d} t} x^{T} P x=-\left(x^{T} Q x+u^{T} R u\right)\tag{4}
d
t
d
x
T
P
x
=
−
(
x
T
Q
x
+
u
T
R
u
)
(
4
)
(?)
P
P
P
是对称矩阵,
P
=
P
T
>
0
P=P^T>0
P
=
P
T
>
0
-
PP
P
的作用
将
(4
)
(4)
(
4
)
带入
(3
)
(3)
(
3
)
有
J=
−
∫
0
∞
d
d
t
x
T
P
x
d
t
=
−
(
x
T
P
x
∣
∞
−
x
T
P
x
∣
0
)
=
−
(
0
−
x
T
P
x
∣
0
)
=
x
T
(
0
)
P
x
(
0
)
(5)
\begin{aligned} J & =-\int_{0}^{\infty} \frac{\mathrm{d}}{\mathrm{d} t} x^{T} P x \mathrm{~d} t \\ & =-\left(\left.x^{T} P x\right|_{\infty}-\left.x^{T} P x\right|_{0}\right) \\ & =-\left(0-\left.x^{T} P x\right|_{0}\right) \\ & =x^{T}(0) P x(0) \end{aligned}\tag{5}
J
=
−
∫
0
∞
d
t
d
x
T
P
x
d
t
=
−
(
x
T
P
x
∞
−
x
T
P
x
0
)
=
−
(
0
−
x
T
P
x
0
)
=
x
T
(
0
)
P
x
(
0
)
(
5
)
当系统稳定时,
t⟶
∞
,
x
⟶
0
t \longrightarrow \infty , x \longrightarrow 0
t
⟶
∞
,
x
⟶
0
可见代价函数只跟初始状态和矩阵
PP
P
有关
带入
u
=
K
x
u = Kx
u
=
K
x
,结合式
(
2
)
(2)
(
2
)
、
(
4
)
(4)
(
4
)
,有
x
˙
T
P
x
+
x
T
P
x
˙
+
x
T
Q
x
+
x
T
K
T
R
K
x
=
0
x
T
A
c
l
T
P
x
+
x
T
P
A
c
l
x
+
x
T
Q
x
+
x
T
K
T
R
K
x
=
0
x
T
(
A
c
l
T
P
+
P
A
c
l
+
Q
+
K
T
R
K
)
x
=
0
(6)
\begin{aligned} \dot{x}^{T} P x+x^{T} P \dot{x}+x^{T} Q x+x^{T} K^{T} R K x & =0 \\ x^{T} A_{c l}^{T} P x+x^{T} P A_{c l} x+x^{T} Q x+x^{T} K^{T} R K x & =0 \\ x^{T}\left(A_{c l}^{T} P+P A_{c l}+Q+K^{T} R K\right) x & =0 \end{aligned}\tag{6}
x
˙
T
P
x
+
x
T
P
x
˙
+
x
T
Q
x
+
x
T
K
T
R
K
x
x
T
A
c
l
T
P
x
+
x
T
P
A
c
l
x
+
x
T
Q
x
+
x
T
K
T
R
K
x
x
T
(
A
c
l
T
P
+
P
A
c
l
+
Q
+
K
T
R
K
)
x
=
0
=
0
=
0
(
6
)
代入
A
c
l
=
A
−
B
K
A_{c l}=A-B K
A
c
l
=
A
−
B
K
可以得到
A
c
l
T
P
+
P
A
c
l
+
Q
+
K
T
R
K
=
0
(
A
−
B
K
)
T
P
+
P
(
A
−
B
K
)
+
Q
+
K
T
R
K
=
0
A
T
P
+
P
A
+
Q
+
K
T
R
K
−
K
T
B
T
P
−
P
B
K
=
0
(7)
\begin{aligned} A_{c l}^{T} P+P A_{c l}+Q+K^{T} R K & =0 \\ (A-B K)^{T} P+P(A-B K)+Q+K^{T} R K & =0 \\ A^{T} P+P A+Q+K^{T} R K-K^{T} B^{T} P-P B K & =0 \end{aligned}\tag{7}
A
c
l
T
P
+
P
A
c
l
+
Q
+
K
T
R
K
(
A
−
B
K
)
T
P
+
P
(
A
−
B
K
)
+
Q
+
K
T
R
K
A
T
P
+
P
A
+
Q
+
K
T
R
K
−
K
T
B
T
P
−
PB
K
=
0
=
0
=
0
(
7
)
将
K
=
R
−
1
B
T
P
K=R^{-1}B^TP
K
=
R
−
1
B
T
P
(暂不推导,见
Q4
)代入,有
A
T
P
+
P
A
+
Q
+
(
R
−
1
B
T
P
)
T
R
(
R
−
1
B
T
P
)
−
(
R
−
1
B
T
P
)
T
B
T
P
−
P
B
(
R
−
1
B
T
P
)
=
0
A
T
P
+
P
A
+
Q
−
P
B
R
−
1
B
T
P
=
0
(8)
\begin{array}{l} A^{T} P+P A+Q+\left(R^{-1} B^{T} P\right)^{T} R\left(R^{-1} B^{T} P\right)-\left(R^{-1} B^{T} P\right)^{T} B^{T} P-P B\left(R^{-1} B^{T} P\right)=0 \\\\ A^{T} P+P A+Q-P B R^{-1} B^{T} P=0 \end{array}\tag{8}
A
T
P
+
P
A
+
Q
+
(
R
−
1
B
T
P
)
T
R
(
R
−
1
B
T
P
)
−
(
R
−
1
B
T
P
)
T
B
T
P
−
PB
(
R
−
1
B
T
P
)
=
0
A
T
P
+
P
A
+
Q
−
PB
R
−
1
B
T
P
=
0
(
8
)
上式也被称为
微分Riccati方程
(Algebraic Riccati Equation ,ARE)
到这一步就可以认为
PP
P
是solvable的了,现在已经有很完善的方法能求解ARE了
Q4.1 LQR控制器设计步骤:
步骤一:根据我们想要的期望状态,初步设计好
Q
Q
Q
,
R
R
R
(一般凭借经验,可以通过迭代不断调整)
步骤二:根据
代数Riccati方程
(由系统矩阵组成的等式),情况下求解矩阵P用的是数值解法,很少的情况可以求其解析解。
步骤三:根据
P
P
P
,得到反馈矩阵
K
K
K
的表达式,得到最优控制序列:
Q5:LQR中做出的…假设?
K
=
R
−
1
B
T
P
K=R^{-1} B^{T} P
K
=
R
−
1
B
T
P
并不是假设,而是推导的结果,过程如下
反馈矩阵K的推导*
如果只是应用LQR方法,那么推导过程
可以不用细看
,记住下面的表达式就可以,现在用matlab或是python中的一些库就可以直接求解,应用时理解K的含义就可以。
推导过程应用到矩阵求导相关公式,推荐一个在线矩阵求导网站:
Matrix Calculus
,可以用来验证自己算的对不对。
推导过程:
观察式
(
7
)
(7)
(
7
)
,
A
,
B
,
Q
,
R
,
P
A,B,Q,R,P
A
,
B
,
Q
,
R
,
P
都是常值矩阵,唯一可变的是
K
K
K
阵,所以问题转换为找到一个
K
K
K
使得代价函数最小,下面用到了一些构造,主要关注带
K
K
K
的部分,求解的想法是要将
K
K
K
包含在一个满足一定约束的式子里面或许可以得到
K
K
K
的计算表达式,一种思路是如果我们可以把含有
K
K
K
的部分转换成类似
(
M
+
N
)
T
(
M
+
N
)
(M+N)^T(M+N)
(
M
+
N
)
T
(
M
+
N
)
的结构,那么要使得代价最小,就会有
M
+
N
=
0
M + N = 0
M
+
N
=
0
,那么
K
K
K
就可以求。
令
R
=
T
T
T
R=T^TT
R
=
T
T
T
,代入式
(
7
)
(7)
(
7
)
,有
A
T
P
+
P
A
+
Q
−
K
T
B
T
P
−
P
B
K
+
K
T
T
T
T
K
=
0
A
T
P
+
P
A
+
Q
−
K
T
B
T
P
−
P
B
K
+
(
T
K
)
T
T
K
=
0
(9)
A^{T} P+P A+Q-K^{T} B^{T} P-P B K+K^{T} T^{T} T K=0\\\\ A^{T} P+P A+Q-K^{T} B^{T} P-P B K+(T K)^{T} T K=0\tag{9}
A
T
P
+
P
A
+
Q
−
K
T
B
T
P
−
PB
K
+
K
T
T
T
T
K
=
0
A
T
P
+
P
A
+
Q
−
K
T
B
T
P
−
PB
K
+
(
T
K
)
T
T
K
=
0
(
9
)
为向
(
M
+
N
)
T
(
M
+
N
)
(M+N)^{T}(M+N)
(
M
+
N
)
T
(
M
+
N
)
$ 上面靠,将目标形式展开:
M
T
M
+
N
T
N
+
M
T
N
+
N
T
M
M^{T} M+N^{T} N+M^{T} N+N^{T} M
M
T
M
+
N
T
N
+
M
T
N
+
N
T
M
,令
M
=
T
K
M=T K
M
=
T
K
,刚好可以满足上面其中一项,剩下的用待定系数,带进去解
N
N
N
的表达式:
M
T
M
+
N
T
N
+
M
T
N
+
N
T
M
=
−
K
T
B
T
P
−
P
B
K
+
(
T
K
)
T
T
K
,
M
=
T
K
⇒
N
T
N
+
K
T
T
T
N
+
N
T
T
K
=
−
K
T
B
T
P
−
P
B
K
(10)
M^{T} M+N^{T} N+M^{T} N+N^{T} M=-K^{T} B^{T} P-P B K+(T K)^{T} T K, M=T K\\\\ \Rightarrow N^{T} N+K^{T} T^{T} N+N^{T} T K=-K^{T} B^{T} P-P B K\tag{10}
M
T
M
+
N
T
N
+
M
T
N
+
N
T
M
=
−
K
T
B
T
P
−
PB
K
+
(
T
K
)
T
T
K
,
M
=
T
K
⇒
N
T
N
+
K
T
T
T
N
+
N
T
T
K
=
−
K
T
B
T
P
−
PB
K
(
10
)
注意
(10
)
(10)
(
10
)
左右并不一定相等,只是为了
让等式右凑出等式左的样子
继续观察,等式两边都有含
K
T
K^T
K
T
项和含
K
K
K
项 ,先用含
K
K
K
项拼凑出
N
N
N
:
N
T
T
K
=
−
P
B
K
⇒
N
=
[
−
P
B
(
T
−
1
)
]
T
⇒
N
=
−
(
T
−
1
)
T
B
T
P
T
=
N
=
−
(
T
−
1
)
T
B
T
P
(11)
\begin{array}{l} N^{T} T K=-P B K \Rightarrow N=\left[-P B\left(T^{-1}\right)\right]^{T} \Rightarrow N=-\left(T^{-1}\right)^{T} B^{T} P^{T}=N= \\ -\left(T^{-1}\right)^{T} B^{T} P \end{array}\tag{11}
N
T
T
K
=
−
PB
K
⇒
N
=
[
−
PB
(
T
−
1
)
]
T
⇒
N
=
−
(
T
−
1
)
T
B
T
P
T
=
N
=
−
(
T
−
1
)
T
B
T
P
(
11
)
将
N
N
N
代入,求剩下的部分:
N
T
N
+
K
T
T
T
N
+
N
T
T
K
=
−
K
T
B
T
P
−
P
B
K
,
N
=
−
(
T
−
1
)
T
B
T
P
(12)
N^{T} N+K^{T} T^{T} N+N^{T} T K=-K^{T} B^{T} P-P B K, \quad N=-\left(T^{-1}\right)^{T} B^{T} P\tag{12}
N
T
N
+
K
T
T
T
N
+
N
T
T
K
=
−
K
T
B
T
P
−
PB
K
,
N
=
−
(
T
−
1
)
T
B
T
P
(
12
)
发现含
K
T
K^T
K
T
项也消掉了,仅剩下不含
K
K
K
的第一项:
N
T
N
=
[
(
T
−
1
)
T
B
T
P
]
T
[
(
T
−
1
)
T
B
T
P
]
=
P
B
R
−
1
B
T
P
(13)
N^{T} N=\left[\left(T^{-1}\right)^{T} B^{T} P\right]^{T}\left[\left(T^{-1}\right)^{T} B^{T} P\right]=P B R^{-1} B^{T} P\tag{13}
N
T
N
=
[
(
T
−
1
)
T
B
T
P
]
T
[
(
T
−
1
)
T
B
T
P
]
=
PB
R
−
1
B
T
P
(
13
)
带到代数Riccati方程中有:
A
T
P
+
P
A
+
Q
+
[
T
K
−
(
T
−
1
)
T
B
T
P
]
T
[
T
K
−
(
T
−
1
)
T
B
T
P
]
−
P
B
R
−
1
B
T
P
=
0
(14)
A^{T} P+P A+Q+\left[T K-\left(T^{-1}\right)^{T} B^{T} P\right]^{T}\left[T K-\left(T^{-1}\right)^{T} B^{T} P\right]-P B R^{-1} B^{T} P=0\tag{14}
A
T
P
+
P
A
+
Q
+
[
T
K
−
(
T
−
1
)
T
B
T
P
]
T
[
T
K
−
(
T
−
1
)
T
B
T
P
]
−
PB
R
−
1
B
T
P
=
0
(
14
)
因为:
x
T
[
T
K
−
(
T
−
1
)
T
B
T
P
]
T
[
T
K
−
(
T
−
1
)
T
B
T
P
]
x
≥
0
(15)
x^T\left[T K-\left(T^{-1}\right)^{T} B^{T} P\right]^{T}\left[T K-\left(T^{-1}\right)^{T} B^{T} P\right]x \ge 0\tag{15}
x
T
[
T
K
−
(
T
−
1
)
T
B
T
P
]
T
[
T
K
−
(
T
−
1
)
T
B
T
P
]
x
≥
0
(
15
)
令
T
K
−
(
T
−
1
)
T
B
T
P
=
0
T K-\left(T^{-1}\right)^{T} B^{T} P = 0
T
K
−
(
T
−
1
)
T
B
T
P
=
0
,可以解出
K
=
R
−
1
B
T
P
K=R^{-1} B^{T} P
K
=
R
−
1
B
T
P
怎么理解u=-Kx
u
=
−
K
x
u=-Kx
u
=
−
K
x
是将输入向量
u
u
u
用状态变量
x
x
x
的线性表达,不妨把这理解为LQR的特征,或者说LQR这一形式就意味着这一假设
稳定性分析
想要分析系统的稳定性,一般采用李雅普诺夫稳定性理论来证明。
首先,定义李雅普诺夫函数:
V
(
x
)
=
x
T
P
x
,
P
=
P
T
P
>
0
(16)
V(x)=x^{T} P x, P=P^{T} P>0\tag{16}
V
(
x
)
=
x
T
P
x
,
P
=
P
T
P
>
0
(
16
)
P
P
P
为正定常数矩阵,所以
V
(
x
)
V(x)
V
(
x
)
是 正定的。(?)
然后,对
V
(
x
)
V(x)
V
(
x
)
求
x
x
x
的一阶导数:
V
˙
(
x
)
=
x
˙
T
P
x
+
x
T
P
x
˙
(17)
\dot{V}(x)=\dot{x}^{T} P x+x^{T} P \dot{x}\tag{17}
V
˙
(
x
)
=
x
˙
T
P
x
+
x
T
P
x
˙
(
17
)
将
x
˙
=
A
x
+
B
u
,
u
=
−
K
x
=
−
R
−
1
B
T
P
x
\dot{x}=A x+B u, u=-K x=-R^{-1} B^{T} P x
x
˙
=
A
x
+
B
u
,
u
=
−
K
x
=
−
R
−
1
B
T
P
x
带入上式,得到:
V
˙
(
x
)
=
x
T
[
A
T
P
−
K
T
B
T
P
+
P
A
−
P
B
K
]
x
(18)
\dot{V}(x)=x^{T}\left[A^{T} P-K^{T} B^{T} P+P A-P B K\right] x\tag{18}
V
˙
(
x
)
=
x
T
[
A
T
P
−
K
T
B
T
P
+
P
A
−
PB
K
]
x
(
18
)
再代入
K
K
K
,得到:
V
˙
(
x
)
=
x
T
[
A
T
P
+
P
A
−
2
P
B
R
−
1
B
T
P
]
x
(19)
\dot{V}(x)=x^{T}\left[A^{T} P+P A-2 P B R^{-1} B^{T} P\right] x\tag{19}
V
˙
(
x
)
=
x
T
[
A
T
P
+
P
A
−
2
PB
R
−
1
B
T
P
]
x
(
19
)
因为通过无限时间LQR设计的
P
P
P
会满足上面的代数Riccati方程
(
8
)
(8)
(
8
)
,带进来,得到:
V
˙
(
x
)
=
−
x
T
[
Q
+
P
B
R
−
1
B
T
P
]
x
(20)
\dot{V}(x)=-x^{T}\left[Q+P B R^{-1} B^{T} P\right] x\tag{20}
V
˙
(
x
)
=
−
x
T
[
Q
+
PB
R
−
1
B
T
P
]
x
(
20
)
因为:
Q
>
0
,
R
>
0
,
P
>
0
Q>0, R>0, P>0
Q
>
0
,
R
>
0
,
P
>
0
,故
V
˙
(
x
)
<
0
\dot{V}(x)<0
V
˙
(
x
)
<
0
, 系统是渐进稳定的。
上面是从别处搬运的,我只是看了一遍公式无误,自己其实也看不太懂
也有一种说法,是说稳定性取决于状态矩阵A的特征值的符号,利用MATLAB语句
[V,F] = eig(A)
求得状态矩阵A的特征值以及对应的特征向量。
当全部为实根的时候,只有它们都小于零,系统才是稳定的。
可控性分析
只要满足一些基本条件,LQR的设计过程就能保证得到一个让系统稳定的反馈控制器。
-
LQR定理
令系统
(A
,
B
)
(A,B)
(
A
,
B
)
可控,
RR
R
和
QQ
Q
都是正定的,则闭环系统
(A
−
B
K
)
( A − B K )
(
A
−
B
K
)
近稳定。注意,不管系统的开环稳定性如何,这都是成立的。
回顾现控的相关知识:可控性可以通过检查可控性矩阵
U=
[
B
A
B
A
2
B
⋯
A
n
−
1
B
]
U=\left[\begin{array}{lllll} B & A B & A^{2} B & \cdots & A^{n-1} B \end{array}\right]
U
=
[
B
A
B
A
2
B
⋯
A
n
−
1
B
]
是否满秩来判断
✨matlab实现LQR可视化
模型介绍
物理模型
我们以经典的一阶倒立摆模型为例,进行建模【模型如图】
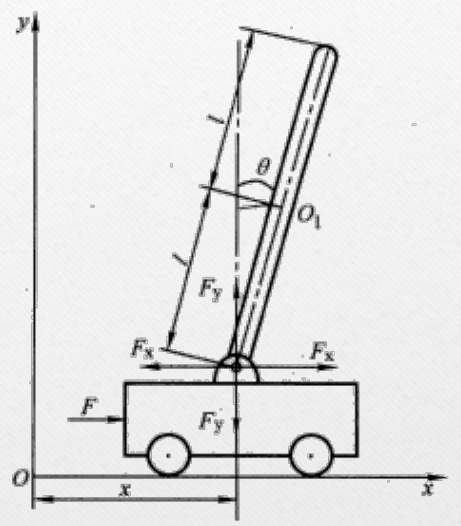
在此模型中,设
| 物理量 | 符号 |
|---|---|
| 滑块质量 |
M M M |
| 摆杆质量 |
m m m |
| 摆杆转动轴心到杆质心长度【半杆长】 |
l l l |
| 摆杆在转轴处转动惯量 |
J J J |
| 小车受到外力 |
F F F |
| 小车位置 |
x x x |
|
摆杆与竖直方向夹角【本文 顺时针 为正】 |
θ \theta θ |
x
=
[
x
1
x
2
x
3
x
4
]
=
[
θ
θ
˙
x
x
˙
]
,
u
=
F
x=\left[\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{array}\right]=\left[\begin{array}{c} \theta \\ \dot{\theta} \\ x \\ \dot{x} \end{array}\right],u=F
x
=
x
1
x
2
x
3
x
4
=
θ
θ
˙
x
x
˙
,
u
=
F
状态方程模型
通过物理建模及化简,最终能得到状态方程
A
、
B
、
C
、
D
A、B、C、D
A
、
B
、
C
、
D
四个矩阵的表达式【表达式推导见第二期】
x
˙
=
A
x
+
B
u
y
=
C
x
+
D
u
(1)
\begin{array}{l} \dot{x}=A x+B u \\ y=C x+D u \end{array}\tag{1}
x
˙
=
A
x
+
B
u
y
=
C
x
+
D
u
(
1
)
代码
% ------------------------------------------
% 本代码使用最经典的一阶倒立摆模型建模
%
% ------------------------------------------
clc;clear;close all;
g = 9.80665;
m = 1;
M = 0.1;
l = 0.18; % 半杆长
J = 1/3 * m * (2 * l)^2;
% ------------------------------------
% 创建一个状态空间模型
A21 = m*g*l*(M+m)/(J*(M+m)+M*m*l^2);
A41 = -m^2*g*l^2/(J*(M+m)+M*m*l^2);
A = [0 1 0 0;
A21 0 0 0;
0 0 0 1;
A41 0 0 0];
% [theta, dtheta, x, dx]
B2 = -m*l/(J*(M+m)+M*m*l^2);
B4 = (J+m*l^2)/(J*(M+m)+M*m*l^2);
B = [0;B2;0;B4];
C=[1 0 0 0;0 0 1 0];
D=[0;0];
% ------------------------------------
% 检验状态空间模型的可控性、稳定性分析
eig(A)
%% Qc=ctrb(A,B)
%% rank(Qc)
Qb=obsv(A,C);
rank(Qb)
% ------------------------------------
% 设计 LQR 控制器
Q = [1 0 0 0
0 1 0 0
0 0 10 0
0 0 0 10];
R = 1;
K = lqr(A,B,Q,R)
% ------------------------------------
% 定义输入信号和时间向量
t = 0:0.02:4;
u = 20 * sin(4*t);
%u = zeros(size(t)) * 0.2;
% ------------------------------------
% 模拟系统的响应
% [theta, dtheta, x, dx]
x0 = [30;0;10;0]; % 初始状态
sys=ss(A-B*K,B,C,D); %经过状态量反馈后的新状态矩阵
[y, t, x] = lsim(sys, u, t, x0);
% ------------------------------------
% 绘制系统的输出信号和状态变量的时间响应
figure;
subplot(2,1,1);
plot(t, u, 'r--', t, y(:,1), 'b-', t, y(:,2), 'r-');
legend('输入信号', '输出信号-theta', '输出信号-x');
xlabel('时间');
ylabel('幅值');
title('系统的输入输出信号');
subplot(2,1,2);
plot(t, x(:,1), 'r-', t, x(:,2), 'b--', t, x(:,3), 'black-', t, x(:,4), 'g--');
legend('theta', 'omega', 'x', 'v');
xlabel('时间');
ylabel('幅值');
title('系统的状态变量');
% =========================================
运行结果
Q单位阵,R=10
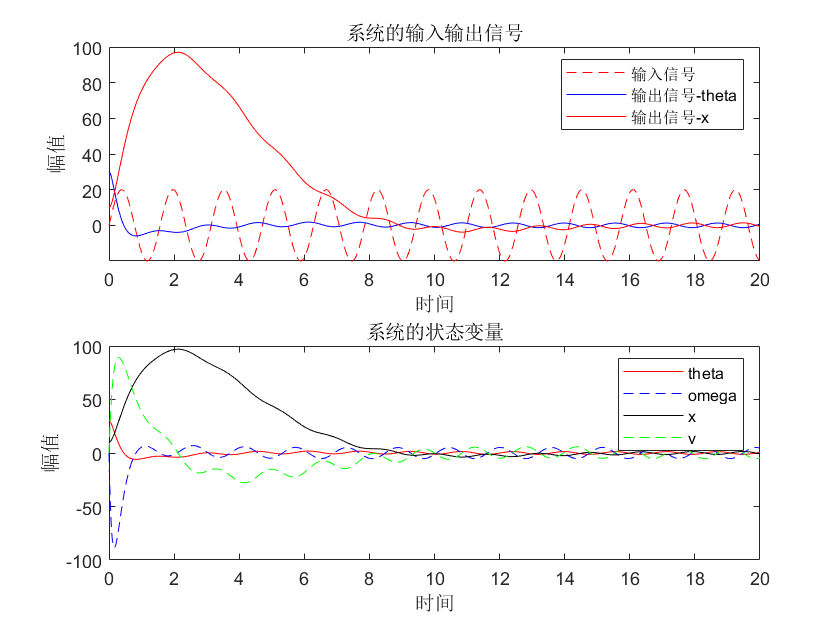
Q为eig(10,1,10,1),R=1
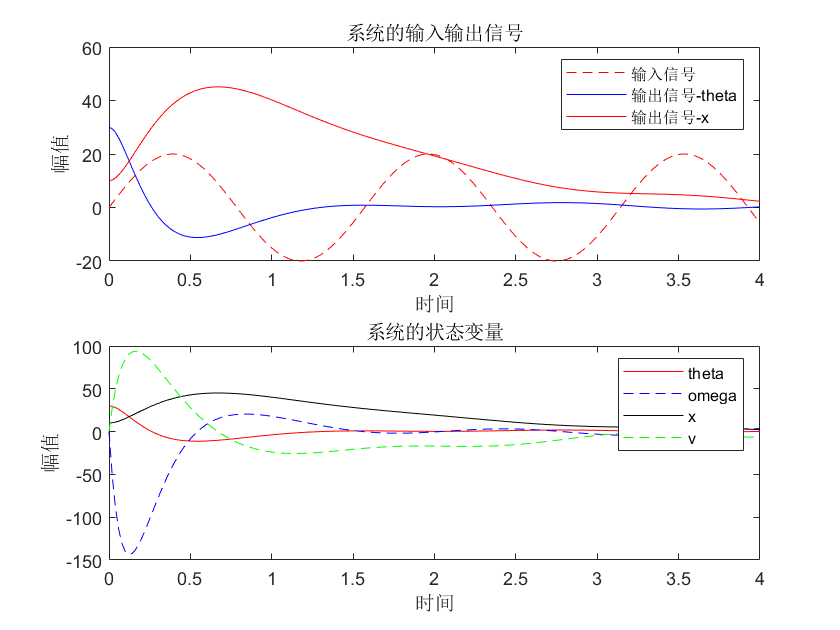
可以发现,输入信号的变化对于状态变量的收敛影响不大。
Q6:稳态误差相关控制
先贴ChatGPT的回答,有待笔者补充完善
Q:如果我想让LQR控制器控制结果中出现可被我准确控制的稳态误差,该怎么做?
回答一:Q后加常数
要让LQR控制器在系统稳定后出现可控的稳态误差,可以在成本函数中添加一个稳态误差的惩罚项。这个惩罚项可以使用系统输出与期望输出之间的偏差来表示。
具体来说,在LQR的成本函数中加入一个与系统输出偏差成比例的惩罚项。这可以通过在
Q
Q
Q
矩阵中增加一个与输出偏差平方成比例的权重来实现。可以通过试验和调整权重的大小,以实现对稳态误差的控制。
以下是一个例子,演示如何在LQR控制器中添加一个稳态误差惩罚项:
假设我们有一个二阶系统,其状态空间表示为:
A = [0 1; 0 0];
B = [0; 1];
C = [1 0];
D = 0;
我们希望控制系统的稳态误差,并使其快速响应。我们可以使用LQR控制器来优化控制器参数,同时在成本函数中添加一个与输出偏差平方成比例的惩罚项。具体而言,我们可以将
Q
Q
Q
矩阵设置为:
Q = [1 0; 0 10];
这样做可以增加对状态
x
2
x_2
x
2
的权重,从而加速系统的响应。然后,我们可以添加一个惩罚项来惩罚输出偏差,例如:
Q(2,2) = Q(2,2) + 1000;
这样可以增加对输出偏差的权重,从而减小稳态误差。
最后,我们可以使用lqr函数计算LQR控制器的增益矩阵,并将其应用于系统:
R = 1;
K = lqr(A, B, Q, R);
sys_cl = ss(A-B*K, B, C, D);
通过这样的设置,LQR控制器将通过调整输入信号来控制系统状态,并在稳态时保持输出与期望输出之间的偏差尽可能小。
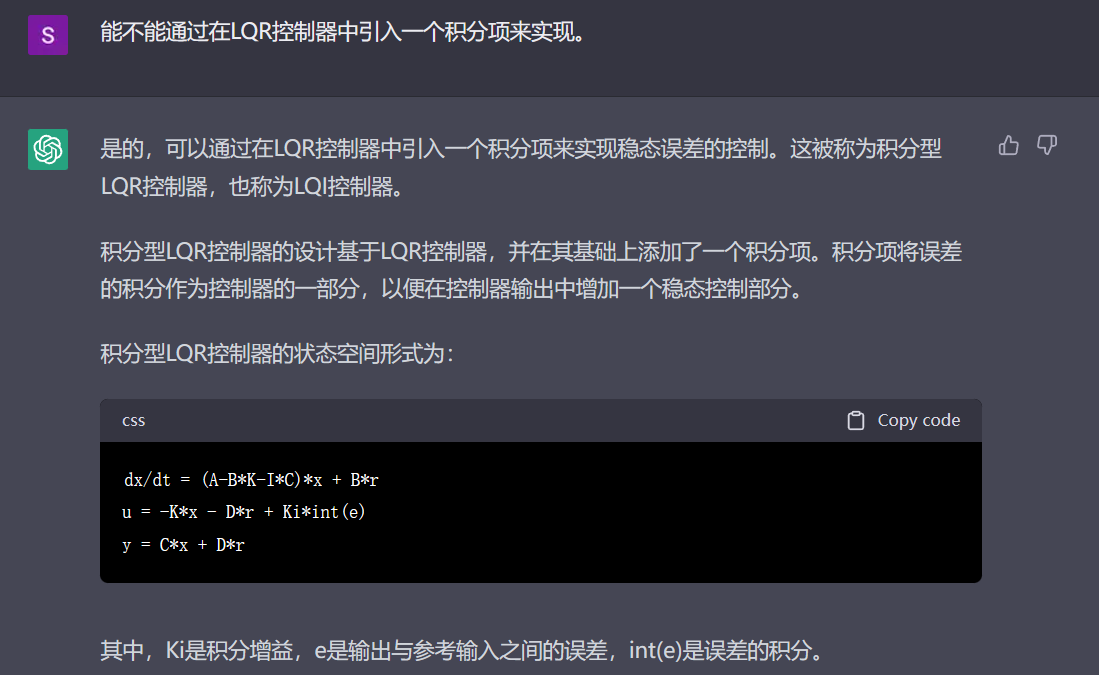
回答二:加入积分项【LQI】


下一期指路
LQR的理解与运用 第二期——一阶倒立摆在matlab上的LQR实现
参考文档
(个人感觉最好✨→)
线性二次型调节器(LQR)原理详解
https://blog.csdn.net/qq_36133747/article/details/123413115
(推导K→)
LQR最优控制方法小结
https://zhuanlan.zhihu.com/p/363033191
(应用篇)
RoboMaster平衡步兵机器人控制系统设计
https://zhuanlan.zhihu.com/p/563048952当时的