
行列式几何意义,
维平行体的有向体积:
任意
法线与最后一个向量的内积,就是
。
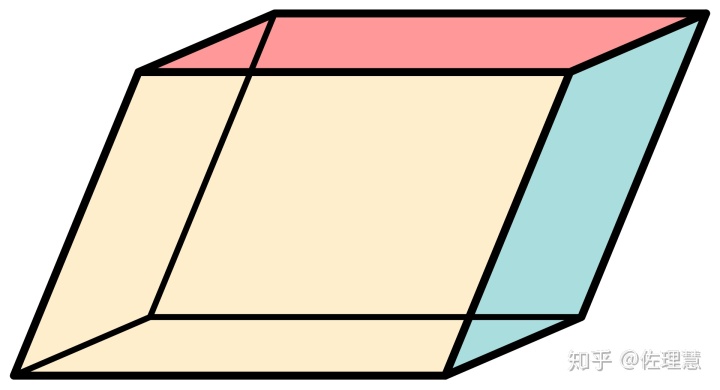
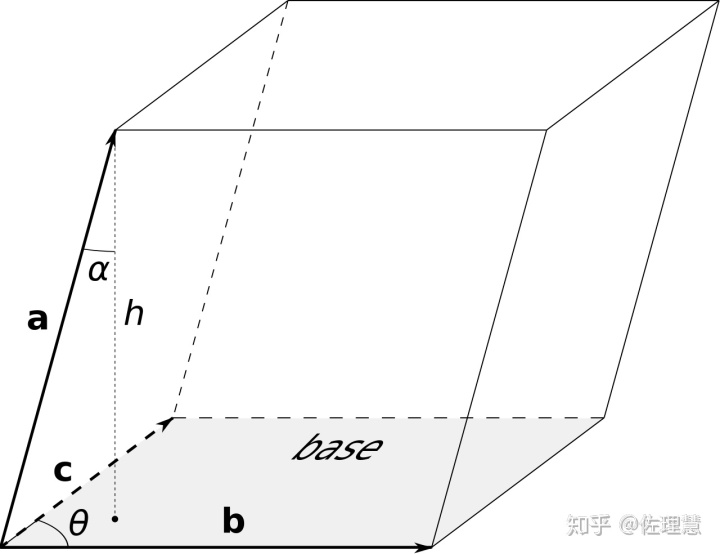
上图中的体积就是:
假设
而
构造下面行列式,高维外积:
利用拉普拉斯展开可以得到:
显然,
其中,
旋转矩阵是正交矩阵。必然存在一个旋转矩阵
其中
此时,
所以
这就归约到
只要当
根据二维叉乘的定义:
多元函数求积分中的变量代换:
当我们计算多元函数积分时
有时候我们会进行变量替换。即使用
其中:
令
如何替换呢?我们在
这就得到了从:
这个矩阵就称之为雅可比矩阵:
根据行列式可以表示
版权声明:本文为weixin_42421284原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。