motivation：

平衡隐私保护和实用性，当用户很多，中心DP有瓶颈。

methods：

LDP+relaxation==》Network DP，local view（local memory and messages received）

experiments

：求和，离散直方图，梯度优化

conclusion：

对比LDP，隐私收益O（1/根号n）；避免用户共谋，在完全图中在LDP下，与相同算法比较提出的算法隐私放大结果O（1/根号n的1/4）

Abstract

1.在LDP中提出了一个relaxation，在图结构中沿这边去交换信息，这种relaxation称为network DP。

2.在求和计算，离散直方图计算，随机梯度下降方法优化做实验。

3.we propose simple algorithms on ring and complete topologies.

1 Introduction

1.每个user保持自己的数据，并且和中心只分享结果。

问题：中心有瓶颈，当参与方很大的时候

LDP背景：each participant (user) does not trust anyone and assumes that an adversary may observe everything that she/he shares。问题：utility great loss。Best possible error under LDP is a factor √n larger than in the centralized model of DP

2.amplify methods：shuffling，subsampling，iteration。这些方法很难应用在联邦/去中心化设置中: the former requires that the identity of the subsampled participants remain secret, while the latter assumes that only the final model is revealed。

1.2 贡献

1.提出的放松LDP只可以观察临近的数据。Network DP也可以解释用户之间碰撞。

2.对于不同任务，提出了simple algorithms，相比于LDP，隐私收益为O(1/√n) 。

3.环图对于用户共谋不够robust，所以提出了完全图（complete graph）。对于求和问题提出了算法，相比于LDP放大结果为

4.对于随机梯度下降优化中，提出了decentralized SGD algorithm。在某些情况下，隐私放大为

nearly matching the utility of centralized private SGD。

5.有趣的是，上述算法可以容忍恒定数量的碰撞，但代价是减少了隐私放大效果。

2.1 Network Differential Privacy

1.

对于图的差分隐私之间的关系是弱于本地差分隐私的，但是提供了更好的隐私保障。但是前者保护的是整个数据集的数据，所以说提供了更好的隐私保障。

A是去中心算法，两个D就是相邻数据集。提出了一个满足（epsilon ,delta）network DP。NetworkDP是被认为讲操作O和算法A结合起来的一种分析，主要就是希望结合起来的隐私要比单独的A要好（与DP比）。

In other words，applying Ov amplifies the privacy guarantees of A.

但是又考虑到用户之间的勾结，根据定义1，假设一个一个upper bound上界c，代表用户可能串通的数量。在这种setting下，希望保护聚集的信息Ov’

2.2 Decentralized Computation on a Walk

T 代表token；X是用户u的局部损失函数在τ处的(随机)梯度；

3 Walking on a Ring

3.1在

有向环图

上的真实求和

边E从第一个用户u开始walk，范围是u到n-1。Token从用户1开始经过k次。背景：环是公开的。在LDP中，在发送数据给中心之前，需要给每一个single contribution添加随机扰动（标准差standard deviation）。所以在这个求和问题中，也是考虑了一个抽象机制Perturb(x; σ) 去添加噪声（高斯机制或者拉普拉斯）Let

σloc

be the standard deviation of the noise required so that Perturb(·; σloc) satisfifies (ε, δ)-LDP。添加的噪声的标准差是满足 (ε, δ)-LDP的。标准差每n-1次添加一次。

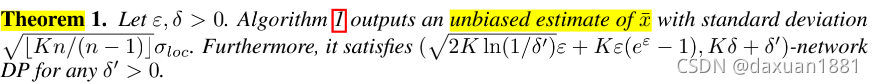
LDP的标准差是

，因此算法1提供了O(1/√n) reduction in error，就等同于O(1/√n) gain in ε。Algorithm 1 achieves the same privacy-utility trade-off as a trusted aggregator 。

注意：算法1假设用户之间是不共谋的。

输出的其实是对于真实值的一个分布，并不是真实数值。

假设用高斯噪声，添加标准差为

全部添加的噪声为

，这就和算法1有一样的utility。

3.2 离散直方图计算

并不是环直方图，是

用户之间的关系

可以看作是一个ring，本质上还是单值的频数估计。

目标：计算

在LDP中，classic的方法就是

L-ary randomized response

（Kairouz, P., Oh, S., and Viswanath, P. (2014). Extremal mechanisms for local differential privacy. In NIPS.）用户以概率为1-y提交真是值，y是均匀随机值，使用RR(y)作为随机扰动。初始化：token用足够的随机元素去隐藏第一个贡献，包含着部分的直方图，等价于shuffling。

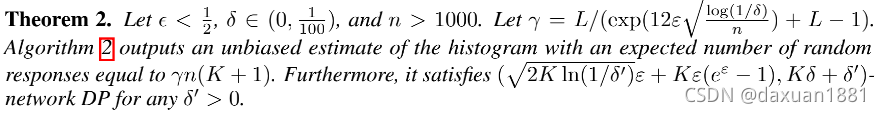
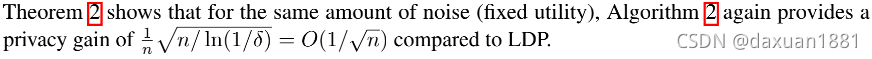
为了简单地表示，定理2依赖于(Amplifification by Shufflfling: From Local to Central Differential Privacy via Anonymity. )，它有一个简单的封闭形式。

3.3 Discussion

局限：1.对于用户共谋算法不够强壮，在算法1假设是不共谋的。如果两个用户串通冰鞋share 他们的信息，算法就不满足DP了。即使加了noise，也没有保护了。当一个用户在两个共谋节点之间，他的隐私保障就会degrade。对于直方图也有类似推理。

2.固定环拓扑不适合扩展到梯度下降，所以准备用iteration进行隐私放大。在这种放大方案中，对给定用户（数据点）的隐私保证随着其之后的梯度步数的增加而增加。因此，在固定环中，用户u相对于另一个用户v的隐私取决于它们在环中的相对位置(例如，当v在u之后时，不会有隐私放大)。这些限制促使我们考虑在一个

完整图（complete graph）

上的随机walk。

4 Walking on a Complete Graph

换句话说，在每一步中，token都被发送给在V中均匀随机选择的用户。我们考虑固定长度的随机行走T > 0，因此给定用户贡献的次数本身是随机的。

4.1 真实求和

用户u接受第k次的token并且用

进行更新，与之前ring中的一样，也是满足LDP。在LDP下，对比了相同的算法，并且得到隐私放大是

求和任务本质：随机选取用户，通过扰动之后叠加。

which relies on the intermediate aggregations of values between two visits of the token to a given user and the secrecy of the path of the token.

我们fix了用户v，并且量化了在token访问的时候，用户u有多少私人数据泄漏给用户v。对v的访问次数遵循二项式定律

我们可以用Nv,以

（无偏性：估计参数的期望为他的真实值）的概率bound住（采用切比雪夫）。在两次访问v之间，行走的步数遵循参数1-1/n的几何定律。我们区分小于根号n/2的小循环和较大的循环。利用霍夫丁不等式，通过

我们bound的了小循环的数量，而且对于每一个小循环的隐私损失最多为

。对于较大的循环，the contribution of u is aggregated with at least √ n/2 others, leading to a privacy loss of at most√2ε/n1/4 . 因为循环对于用户v是保密的，所以可以看作是在n-1个选择中替换根号n/2个用户用作下采样（subsampling）。用采样方法去bound隐私损失。

4.2离散直方图计算

4.3使用随机梯度下降做优化 （不看）

5 Experiments

理论界限的比较。

我们数值计算了定理3对于实求和任务(算法3)的理论边界，并将其与局部DP进行了比较。回想一下，用户贡献的数量是随机的(期望值为T /n)。因此，为了提供网络DP和本地DP之间的公平比较，我们推导了一个类似定理3的本地DP，我们使用相同的Chernoff界来控制用户贡献的数量，并使用高级合成来衡量总的隐私损失。此外，为了隔离贡献数量的影响(这在网络DP和本地DP中是相同的)，我们还报告了在假设每个用户贡献固定次数T /n下得到的边界。图1a绘制了变化n的边界的值。我们看到，当n > 100时，我们的理论结果提供了与局部DP相比的增益，并且这些增益随着n的增加变得越来越显著。我们注意到，在每个用户贡献的固定数量下获得的曲线也表明，在边界内更好地控制Nv可以使我们的放大结果明显更紧凑。

经验行为的差距

。我们的形式分析包括控制用户贡献的数量，以及使用集中不等式控制周期的大小，这导致了一些近似。然而，在实际部署中，可以使用这些数量的实际值来计算隐私损失。因此，我们研究了我们的理论隐私保障和通过运行随机walk的模拟可以在实践中获得的差距。具体来说，我们对大小为T = 100n的随机walk进行采样。然后，对每一对用户，根据实际行走的特点和高级组合机制计算隐私损失。我们在10次随机漫步中重复这个实验，然后我们可以报告在所有用户对和所有随机运行中观察到的平均、最好和最坏的隐私损失。图1b报告了基于高斯机制的真实求和情况下的经验结果，其中隐私以因子√m增长，其中m为元素聚集在一起的数量(即，我们观察到，网络DP实现的增益在实践中明显强于我们的理论边界保证(见图1a)。特别是，即使对于较小的n，增益也是显著的。这些结果再次表明，在我们的分析中还有改进的空间，例如诉诸于更好的集中界限。

我们对离散直方图计算进行了类似的实验，这些实验证实，通过去中心化来扩大隐私的经验收益对于这项任务也很重要，参见附录F。