前言

为了与课本那难以理解的表述区分，部分定义会用自己的话来解释，以课本为准。

谓词逻辑

命题符号化

存在量词 与 合取 搭配

全称量词 与 蕴含 搭配

析取、合取范式

只要看式子中连接每一项的连接词是∧还是∨，连接词是∧则式子为合取范式，为∨是析取范式。

前束范式

量词（全称、存在）都在前面。

1、使用换名规则：

2、分配律

全称量词 对 合取 有分配律

存在量词 对 析取 有分配律

3、蕴含等值式（p->q）

前件p，后件q

p的量词做结合律要取反

q的量词做结合律保持不变

例题1

例题2

构造推理证明

9条推理定律

对于附加律和化简律：

附加律中：A是前提，也就是A为真，所以（A V B）一定也为真：

化简律中：（A ^ B）是前提，也就是A和B都为真，所以A一定为真

全称量词与存在量词 的 添加与消去

∀xA(x)：x是指导变元，A是辖域

举例：

例题1

例题2

集合

对称差

​ A ⊕ B = ( A U B ) – ( A ∩ B )

广义并、广义交

广义并：集合A元素的元素 构成的 集合。

特殊的，当元素不是集合时（就没有元素的元素了）：

A = { {a,b,c} , a , {d,e} }

UA = a U { a,b,c,d,e }

广义交：集合A所有元素的公共元素 构成的集合。

特殊的，当元素不是集合时（就没有元素的元素了）：

A = { {a,b,c} , a , { c,d,e} }

∩ A = a ∩ { c }

包含排斥原理（容斥原理）

例如全集是：S = A U B U C

|S| = |A| + |B| + |C| – ( |A∩B| + |A∩C| + |B∩C| ) + |A∩B∩C|

例题1

例题2

关系

< x,y >

x称为第一元素

y称为第二元素

R为A上的关系：R中的关系的元素都是A中的元素，也就是如果<x,y>∈R，x和y必须∈A

关系运算

复合运算（左复合、右复合）

运算技巧

另一种写法：

• R○R就是R²，将R写两遍（2次幂，n次幂就写n+1遍）。
• 列出R的所有元素（第一元素和第二元素）
• 将R中的二元关系用线连接
• 只看有连续连接的线（这里【第二层】的1并没有上一层的元素与它相连，所以不用再看它）

三种性质

R为A上的关系

自反、对称，传递

自反：R中任意一个元素x，都有<x,x>在R中，则R是自反的，否则R是反自反的。（说明I_A⊆R，R就是自反的，否则是反自反）

对称：对R中的所有元素进行【逆运算】（对调第一元素和第二元素），如果逆运算后的元素不在R上，则R是反对称的，否则是对称的。

传递：R中的两个元素<x,y>和<y,t>，如果R中有<x,t>说明R是传递的，否则就不是。

闭包

自反、对称、传递闭包：拥有这些性质的集合，且集合元素的数量最少。

一般地，R的自反闭包记作 r® ，对称闭包记作 s® ，传递闭包记作 t® 。

• 1）r® = RUR⁰

• 2）s® = RUR^-1

• 3）t® = RUR¹UR²UR³U…

集合元素最少的意思是，只要满足性质就可以，不需要额外的元素。

等价关系

R是A上的关系，如果R是自反的、对称的和传递的，那么称R为A上的等价关系。

虽然课本上这么写，但看了等于没看。

通俗的讲：

如果R是A上的等价关系，R中的某两个个关系是<x,y>，<y,z>。

• 自反：x和x自己是等价的。

• 对称：如果x和y是等价的，那么y和x也一定是等价的。

• 传递：如果x和y是等价的，y和z是等价的，那么x和z是等价的。

还没懂？

有人会说，地球上还有其他水果，是的，但是画不完 ：）

那么苹果和西瓜都是等价的（都是水果），西瓜和橙子也是等价的，当然苹果和橙子也是等价的咯。

例题1

商集

商集就是等价类作为元素的集合。

例题1中的商集为 { {1,4,7},{2,5,8}, {3,6} }。

偏序关系

偏序关系是自反的、反对称的、传递的。

如果<x,y>∈R，那么x≼y，读作x“小于等于”y，注意“小于等于”并不是数值意义上的，而是根据R的定义。

• 为什么是反对称？

• 可比

如果<x,y>在偏序关系R中，那么称x和y是可比的，否则称作不可比。

例题1

特别的，如果A中所有的元素在R中都是可比的，称R为A上的全序关系。

哈斯图

覆盖：

如果偏序集A中存在<x,y>，但是不存在<x,z>和<z,y>，那么称y覆盖x。

也就是x和y没有中间元素。

举个例子：

R为A = { 1,4,6 }上的整除关系，则称4和6覆盖1；

如果A = { 1,2,4,6 }，那么4和6就没有覆盖1了，因为1整除2（即<1,2>）而2都能整除4和6（即<2,4>，<2,6>）。

哈斯图能够直观的表示偏序集合的关系。

如果<x,y>在偏序集中，那么x在y的下方。

哈斯图中不同的两个元素x和y，如果y覆盖x，那么就用一条线段连接。

例题1

最小元、极小元

当然也有最大元和极大元。

• 最小元：比所有元素都小，体现在R中的<x,y>，最小元是x，y必须是其他所有元素。

• 极小元：没有比它更小的元素，体现在R中的<x,y>，只要极小元出现，必然在x位置。

例题1

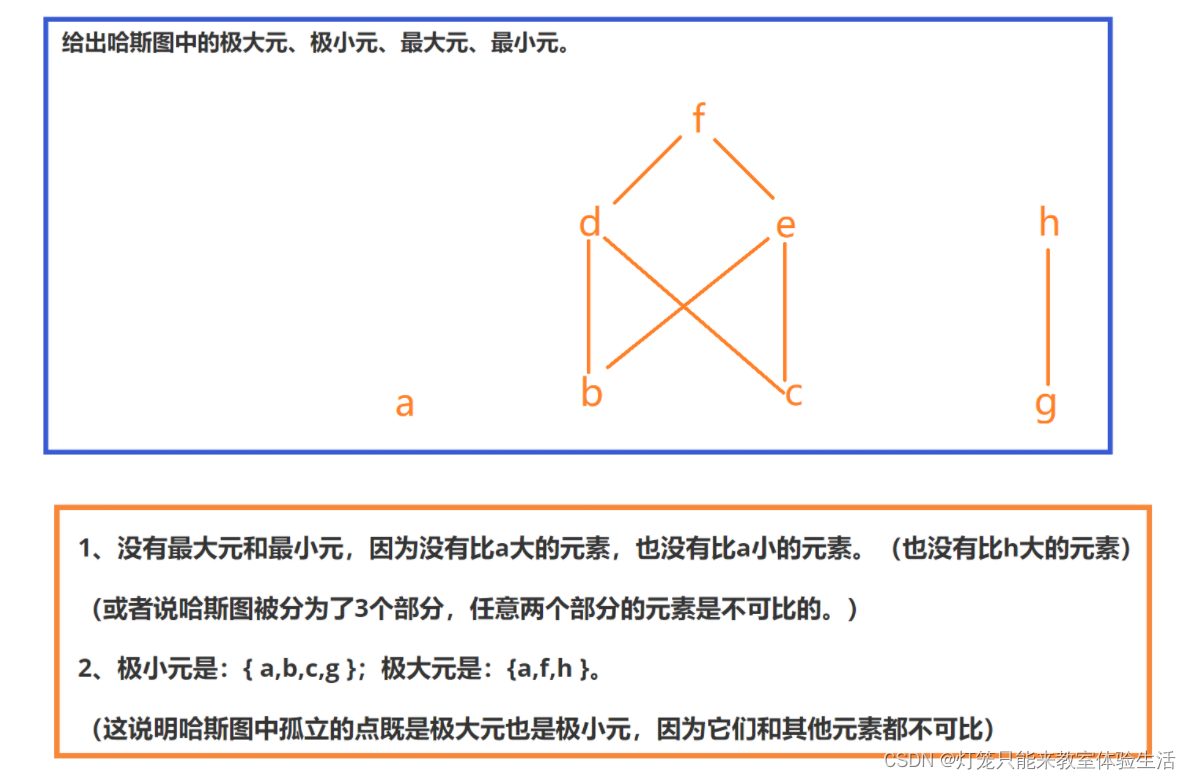
上界、最小上界

当然也有下界和最大下界了。

• 上界：大于等于B中的所有元素组成的集合。

• 最小上界（也称作上确界）：上界的最小元，因为上界是相对的，所以大于等于B的元素也可能小于某些元素。

例题1

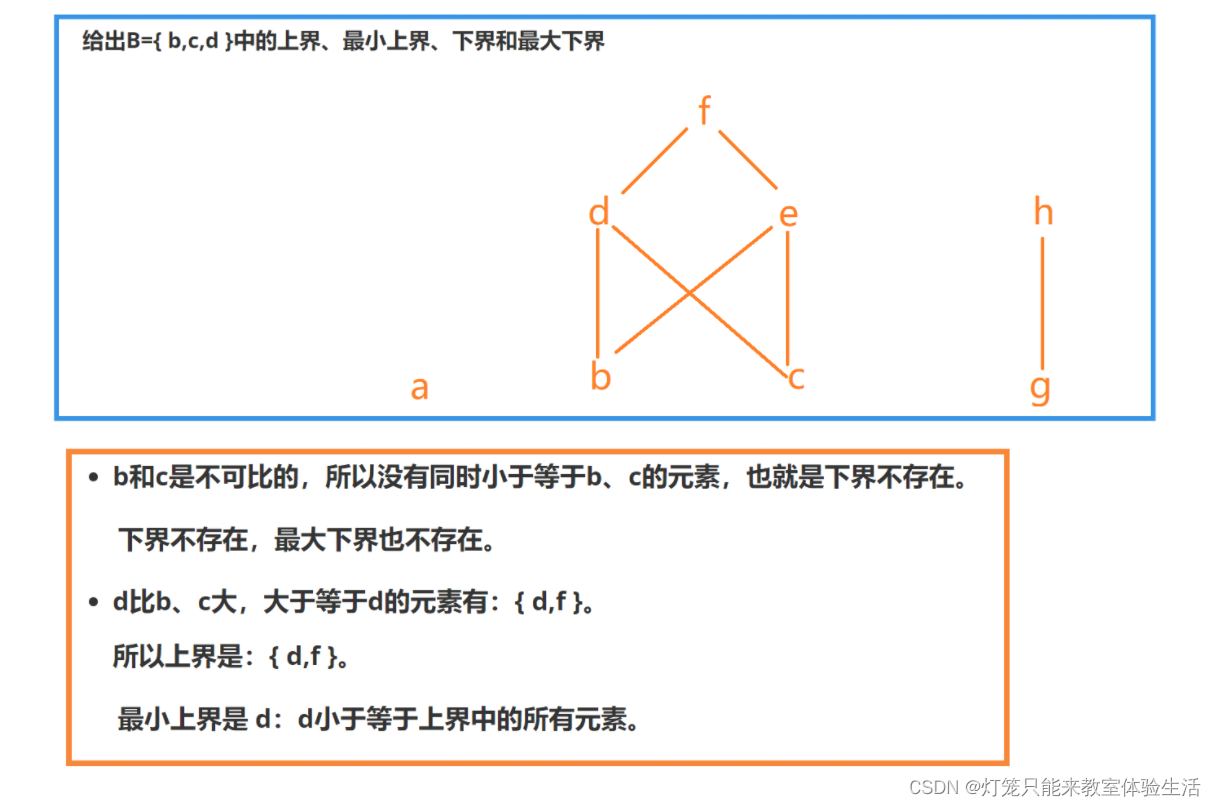
函数

对于二元关系F，如果任意一个x∈domF，并且只存在着一个y∈ranF，使得xFy成立，那么F是函数。

• domF 表示 F中的第一元素，也就是<x,y>中的x。
• ranF 表示 F中的第二元素，也就是<x,y>中的y。

像与完全原像

一个函数f：A->B（A是函数的定义域domf，B是函数的值域 ranf）。

• 如果 A₁ ⊆ A，则 f(A₁) = { f(x)| x∈A₁ }，也就是A₁中所有元素对于的值。特别的，如果A₁ = A，那么称 f(A)为函数的像。
• 如果 B₁ ⊆ B，则 f^-1(B₁) = { f(x)| x∈A ^ f(x)∈B₁ }，也就是B₁中所有元素对于的自变量（键值对中的键）。特别的，如果B₁ = B，那么称 f^-1(B)为函数的完全原像像。

例题1

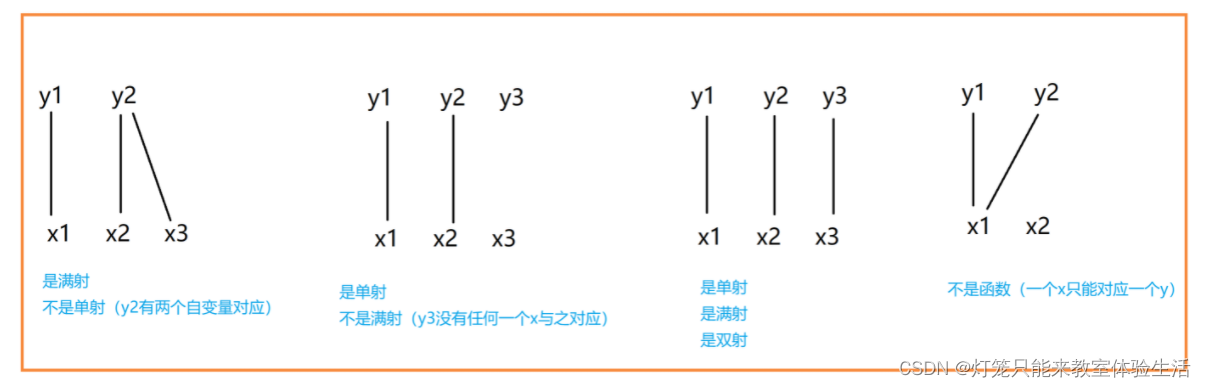
满射、单射、双射

设 f : A->B,f有<x,y>

• 如果ranf = B，那么f是满射的。也就是说所有的 y 都有一个 x 与之对应。

• 如果任意的 y 都只有一个 x 与之对应，那么f是单射的。

• 如果既是满射又是单射，称为双射

复合函数

设F和G都是函数，那么F○G也是函数，称作复合函数（F与G复合）。

设 H = F○G

domH = { x| x∈domF ^ F(x) ∈domG }，也就是 H(x) = G( F(x) )。

推论

如果f : A->B，g : B->C都是满射，那么 f○g : A->C 也是满射。

如果f : A->B，g : B->C都是单射，那么 f○g : A->C 也是单射。

如果f : A->B，g : B->C都是双射，那么 f○g : A->C 也是双射。

反函数

f : A->B，f的反函数 f^-1 : B -> A，也就是函数的值域是反函数的定义域，函数的定义域是反函数的值域。

图

图是由顶点集和边集组成的。 ——-沃兹基·硕德

图的概念多的可怕。 ——-沃兹基·硕德

超多概念 ：）

• 图的顶点个数称为图的阶，n个顶点的图叫n阶图。

• 没有边的图叫零图。

• 没有顶点的图叫空图。

• 只有一个顶点的图称为平凡图。

• 如果给边和顶点指定一个记号，称这样的图为标定图。

• 将有向图的边改为无向边后的图称为基图。

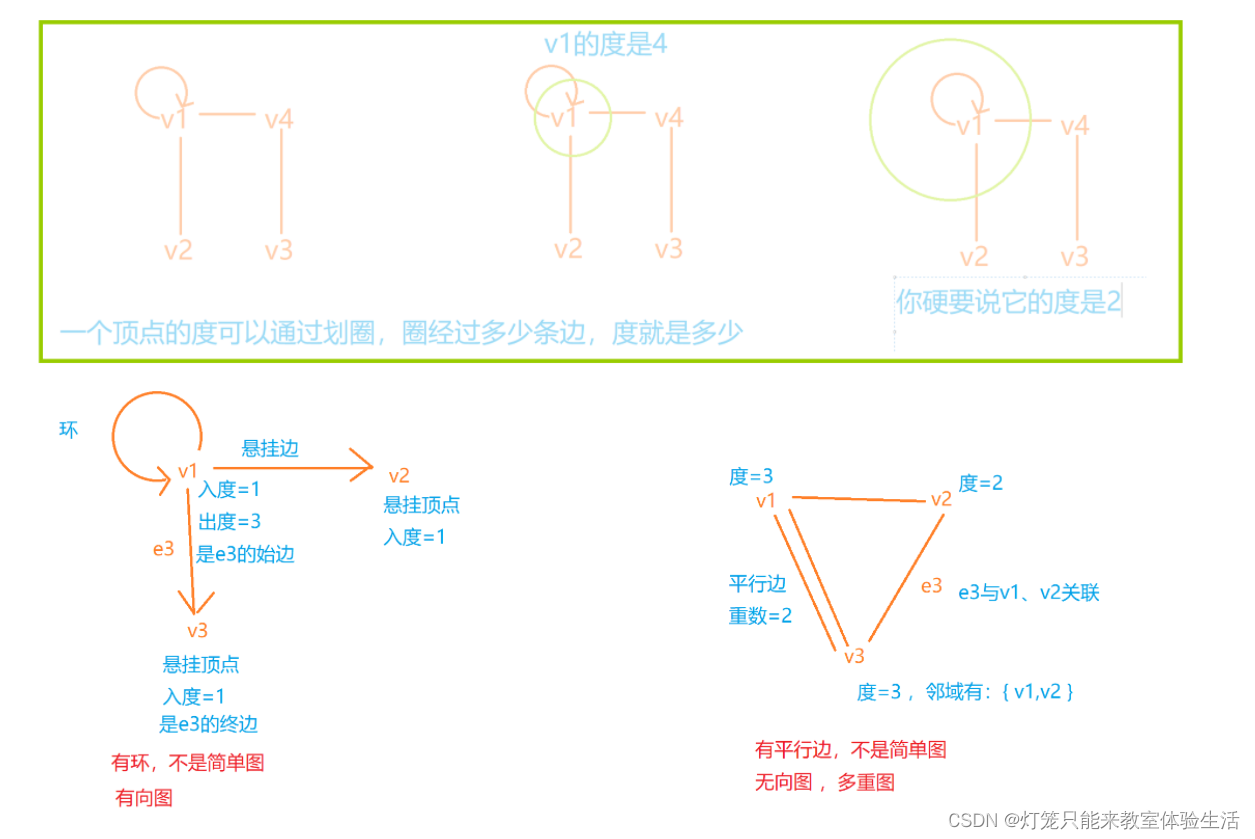
• 边e有两个端点<v₁，v₂>，称e与v₁，v₂关联，如果v1≠v2，则称e与v₁，v₂的关联次数为1，

  如果v₁= v₂ = v，称关联次数为2，如果 v₃不是边的两个端点中的任何一个，则称e与v₃的关联次数为0。

• 如果两个顶点之间有边，则这两个顶点相邻。

• 如果一条边的两个端点相同，则这条边称为环。

• 与一个顶点v相邻的 顶点集 称为v的邻域。

• v的领域加上v，称为闭邻域。

• 与v关联的边（包括环），组成的集合称为关联集。

• 如果关联一对顶点的无向边多于1条，称这些边为平行边。

• 平行边的条数称为重数。

• 含有平行边的图称为多重图。

• 没有平行边和环的图，称为简单图。

• 无向图中 v 作为边端点的次数称为 v的度，记作d(v)。

• 有向图中 v 作为边的始点的次数称为 v的出度，记作d⁺(v)。

• 有向图中 v 作为边的终点的次数称为 v的入度，记作d^–(v)。

• 有向图中d⁺(v) + d^–(v) 称为 有向图的度。

• 无向图中，度最大的顶点的 度 称为最大度。

• 无向图中，度最小的顶点的 度 称为最小度。

• 有向图中，出度最大的顶点的 出度 称为最大出度。

• 有向图中，出度最小的顶点的 出度 称为最小出度。

• 有向图中，出度最大的顶点的 入度 称为最大入度。

• 有向图中，出度最小的顶点的 入度 称为最小入度。

• 称度为1的顶点为 悬挂顶点。

• 与悬挂顶点关联的边称为悬挂边。

握手定理

• 无向图中，所有顶点的度数之和 = 边数的两倍。
• 有向图中，所有顶点的度数之和 = 边数的两倍。
• 有向图中，所有顶点的入读之和 = 所有顶点的出度之和 = 边数。
• 握手定理推论：任何图中，奇度顶点的个数是偶数。

为什么叫握手，而不是握脚呢(●’◡’●)

• 因为握手，至少要两个人（好好好，你可以自己和自己握手）。

• 而人们伸出的手握在一起相当于边，人相当于顶点。

• 如果是有向图可以理解为A向B伸手（A伸出的手是出度），每握一次手（一条边，边关联两个点），需要两只手（度数）。

• 人伸出手的数量=握手次数的2倍。

• 如果一个人和3个人握手怎么办？………………

又是超多概念 ：|

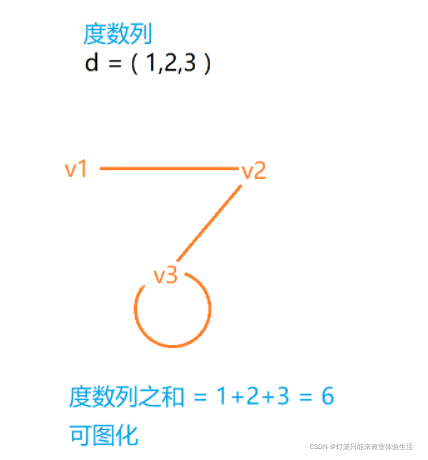
• 无向图中，顶点集V的度组成的数列称为度数列，d(v_i) = d_i。

• 以V为顶点集的图，并且度与V的度数列d对应，称d是可图化的。

• 如果通过d图化后的图是简单图，那么称d是可简单图化的。

• 度数列可图化的充分必要条件是度数列之和为偶数。

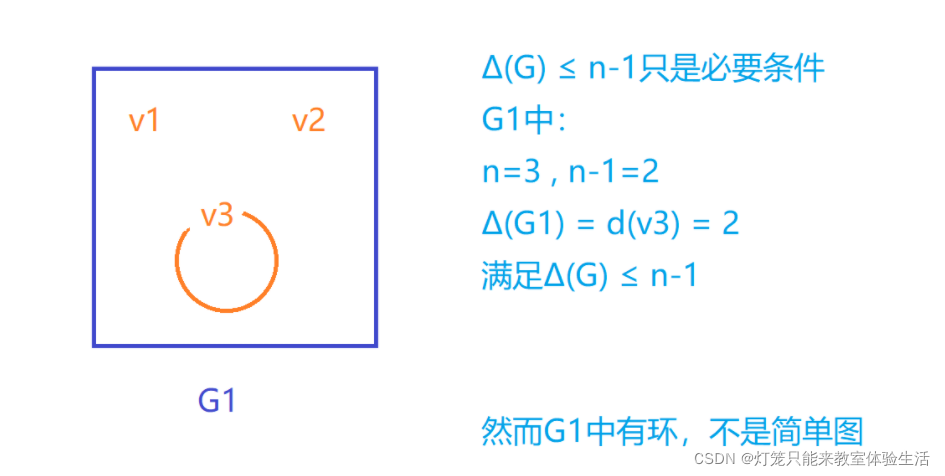
• 如果G是n阶无向简单图，则Δ(G) ≤ n-1（G有n个顶点，G的顶点中最大度不超过n-1）。

• G为n阶无向简单图，若G中每个顶点都与剩余的顶点相邻，则称G为n阶无向完全图，简称为n阶完全图。
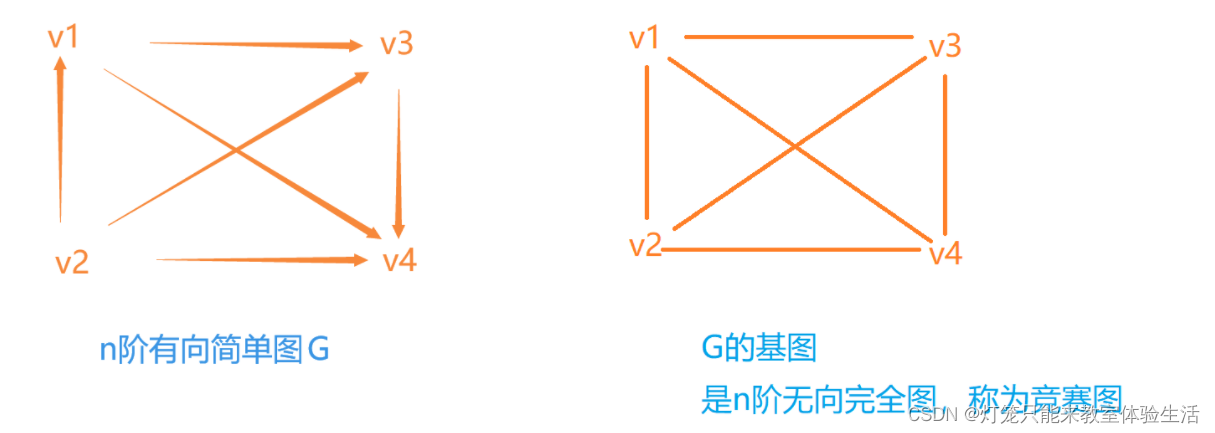
• G为n阶有向简单图，如果G中的每个顶点都邻接到（该顶点做始点）其余顶点，则称G为n阶有向完全图。
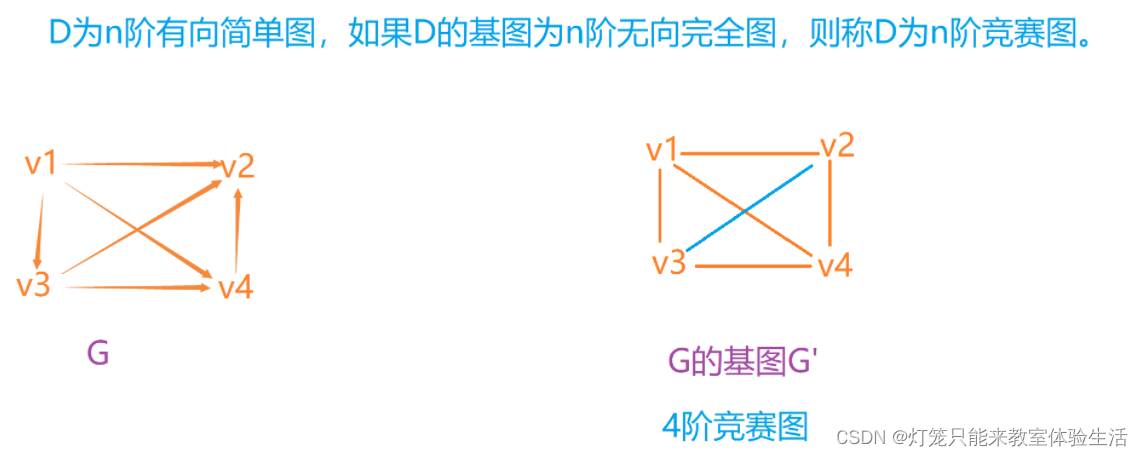
• D为n阶有向简单图，如果D的基图为n阶无向完全图，则称D为n阶竞赛图。
• 两个图的顶点集合之间能够建立一一对应的映射，对应的顶点之间保持边的一一对应关系。那么称这两个图同构。（一个图的邻接矩阵经过有限次的互换行或列的变换变成另一个图的邻接矩阵，则两个图同构。）
• 若G为n阶无向简单图，G中的顶点均有d(v)=k【顶点v的度为k】，那么称G为k-正则图。

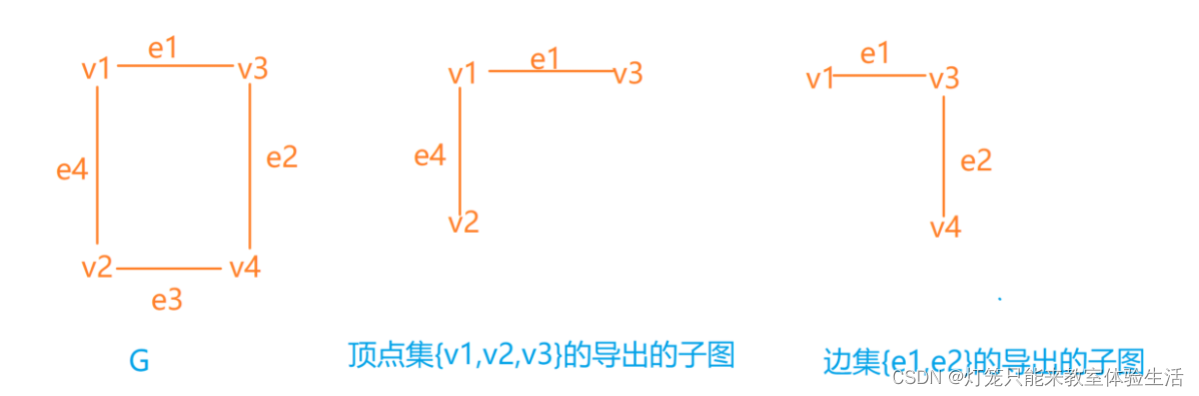
• 如果从图G中抽出一部分顶点，再抽取出与这些顶点相邻的边，那么这些被抽出的顶点和边组成的图G’ 称为G的导出的子图，

  G称为G’ 的母图。

• 从n阶图G中抽取顶点集V（|V|<n，|V|表示顶点集中顶点的个数），再从V中选取端点都在V中的边，组成的图为V的导出的子图。

• 从n阶图G中抽取 边集E（|E|<n），再从E中选取端点都在E中的顶点，组成的图为V的导出的子图。

• 顶点集的导出的子图为G[V]，边集的导出的子图为G[E]。

  

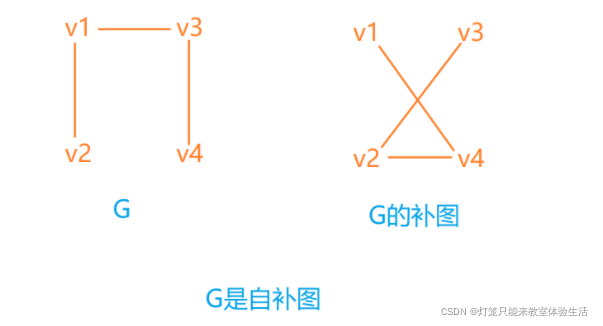
• 自补图是相对于完全图来说，把一个图添加边使其成为完全图所构成的图叫补图。

• 当一个图和它的补图相同（同构）时，为自补图。

• 自补图不一定是完全图，完全图没有自补图。

  

通路与回路

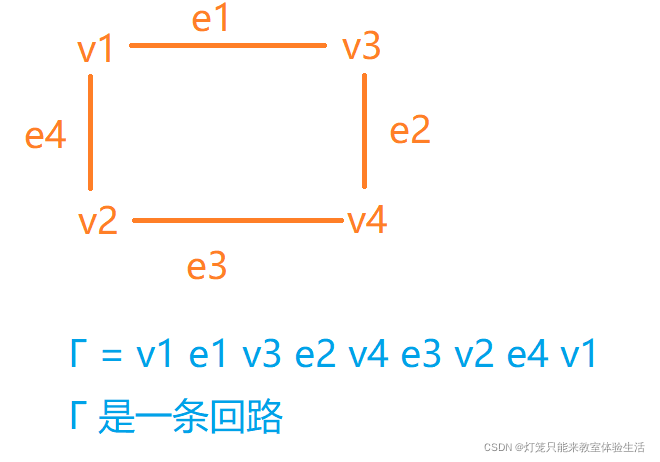
• 设G为无向标定图，给G的顶点和边用下标标记，G中的顶点和边的交替序列 Г = v₁e₁v₂e₂v₃…v_i 称为v₁到v_i的通路。
• 如果一个通路的始点和终点相同，称这个通路为回路。
• Г 中边的个数称为 长度。
• 如果 Г 中没有重复的边，那么称 Г 为简单通路。
• 如果 Г 是一个简单通路，并且 Г 的始点和终点相同，那么称 Г 为简单回路。
• 如果 Г 中没有重复的顶点（除了始点和终点），也没有重复的边，那么称 Г 为初级通路 或者 路径。
• 如果 Г 是一个初级通路，并且 Г 的始点和终点相同，称 Г 为初级回路 或者 圈。
• 具有圈的图称为圈图，规定圈图的顶点个数n≥3。
• 如果 Г 中有重复边出现，称 Г 为 复杂通路，若又有始点和终点相同，称 Г 为 复杂回路。

连通性

无向图的连通性

• 如果两个顶点 u 和 v 之间存在通路，那么称u，v是连通的，记作u~v。

• 如果无向图G是平凡图，或者G中任意两个顶点都是连通的，那么称G为连通图，否则称G为非连通图。

• 如果一个无向图G中的子图D，D是连通图，D是G中连通关系的一个等价类，那么称D为G的一个连通分支。

• 无向图G的连通分支数记作p(G)。

• 无向图G中的任意两个顶点u和v，如果u~v（u和v是连通的），那么称u，v之间长度最短的通路为u，v之间的短程线，短程线的长度称为u和v之间的距离，记作d(u,v)。特别的，当u和v不连通时，d(u,v) = ∞ 。

• 无向图G中的一个顶点集V，如果去掉V后，p(G-V) < p(G)，也就是连通分支数（p(G)）减少了，那么称这个顶点集为点割集。

  • 点割集可能有多个。

• 如果割点集只有一个顶点，那么称这个顶点为割点。

• 无向图G中的一个边集E，如果去掉V后，p(G-E) < p(G)，也就是连通分支数（p(G)）减少了，那么称这个边集为边割集。,边割集简称割集。

• 如果边割集中的边只有一条，称这条边为 割边 或者 桥。

• 如果无向连通图G不是完全图，则称 k(G) = ”点割集中 顶点数量 最少的 集合 的顶点数“ 为G的点连通度，简称连通度。

  （比如点割集为{ { v1 }, { v2,v3 }, { v4,v5,v6 } }，那么数量最少的割点集是{ v1 }，割点数就是1 ）

  • k(G)有时简记为k

• 完全图的点连通度为n-1，非连通图的点连通度为0，那么删除任意k-1个点，图仍然是连通的。

• 如果k(G) ≥ N，则称G为N-连通图，N为非负整数。

  • 如果一个图是4-连通图，那么它也是3-连通图、2-连通图、1-连通图。

• 无向连通图G，λ(G) = “边割集中 边数量 最少的 集合 的边数” 称为边连通度。

• 如果 λ(G)≥N，称G是N边-连通图。

• 如果G是R边连通图，那么删除任意R-1条边，图仍然是连通的。

• 完全图的边连通度=n-1。

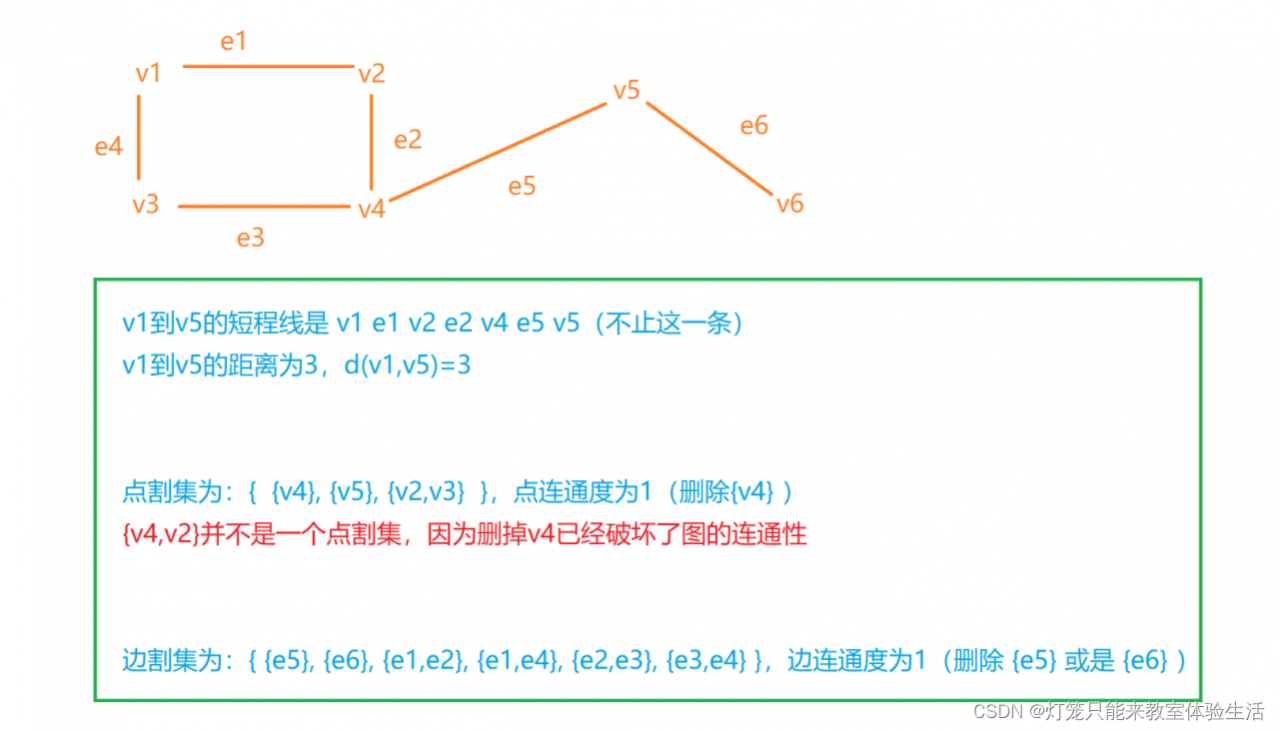
连通度可以体现一个图的连通性。（废话）

如何简单的理解连通度？

连通度体现在：要破坏一个图的连通性，至少要删除 k（点连通度）个点，或者至少要删除掉 λ-1 条边（边连通度）。

有向图的连通性

• 有向图D中，如果u到v存在通路，称u 可达 v，记作 u→v。
• 规定任何一个顶点是可达自身的。
• 如果u可达v，并且v可达u，那么称u和v是相互可达的，记作u↔v。
• 如果u→v（u可达v），那么称u到v的最短通路为短程线，短程线的长度称为u到v的距离。
• 如果有向图D的基图（将有向边变成无向边）是连通图，那么称D为弱连通图，简称连通图。
• 如果D中的任意两个顶点，至少其中一方到另一方是可达的（不要求相互可达），那么称D为单向连通图。
• 如果D中的任意两个顶点，都是相互可达的，那么称D为强连通图。

一些判定定理：

• 有向图D是强连通图的充分必要条件是D中存在经过每个顶点至少一次的回路。
• 有向图D是单向连通图的充分必要条件是D中存在经过每个顶点至少一次的通路。

定义它又来了 ：（

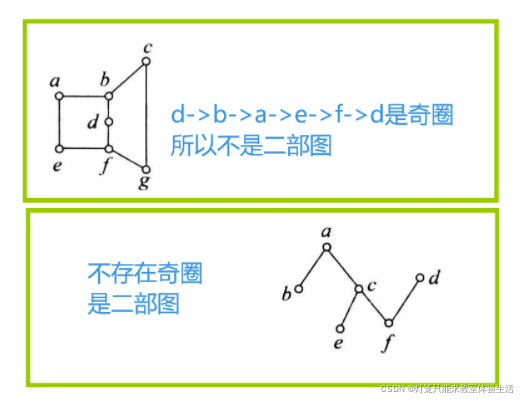
• 如果能将一个图的顶点集划分成两个（V₁、V₂），图中的任意一条边的两个端点一个属于V₁，另一个属于V₂，那么称G为二部图（或者叫二分图、偶图）。
• 如果一个图是简单二部图，并且V₁中的顶点都与V₂中的顶点相邻，那么称这个图为完全二部图，记作K_r,s ，其中 r=|V₁|，s = |V₂|。（也就是V₁和V₂中的顶点个数）。

判定定理：

• 图G是二部图的充分必要条件是G中无奇圈。（也就是G中至少有两个顶点，并且所有的回路长度都是偶数，因为奇圈就是长度为奇数的回路）。

  

图的矩阵表示

别怕，就3个矩阵：关联矩阵、邻接矩阵、可达矩阵。

关联矩阵

无向图的关联矩阵

• 关联矩阵的元素 m_ij 表示i和j的关联次数（顶点在边的端点中出现n次，关联次数就是n，如果一条边是环，那么顶点关联次数是2）。
• 关联矩阵的大小由顶点个数和边的个数决定（废话）。
• 关联矩阵的行 = 顶点个数，列 = 边个数。
  

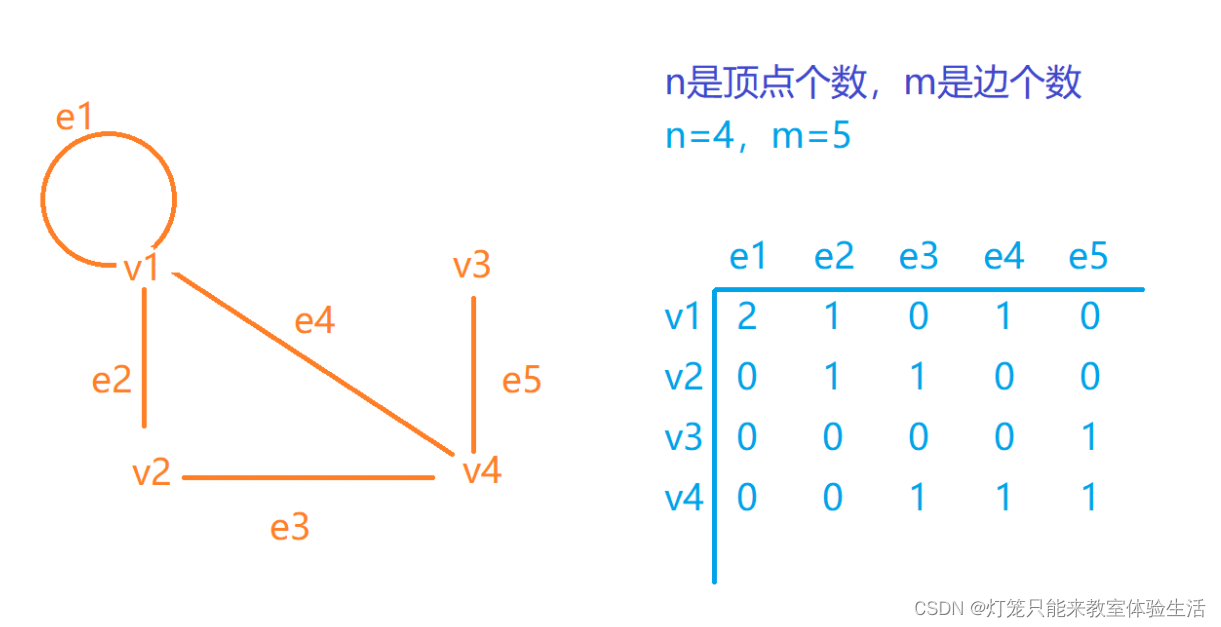
有向图的关联矩阵

无环、无环、无环！

• 矩阵的结构和无向图相同，但是矩阵元素的值有区别。

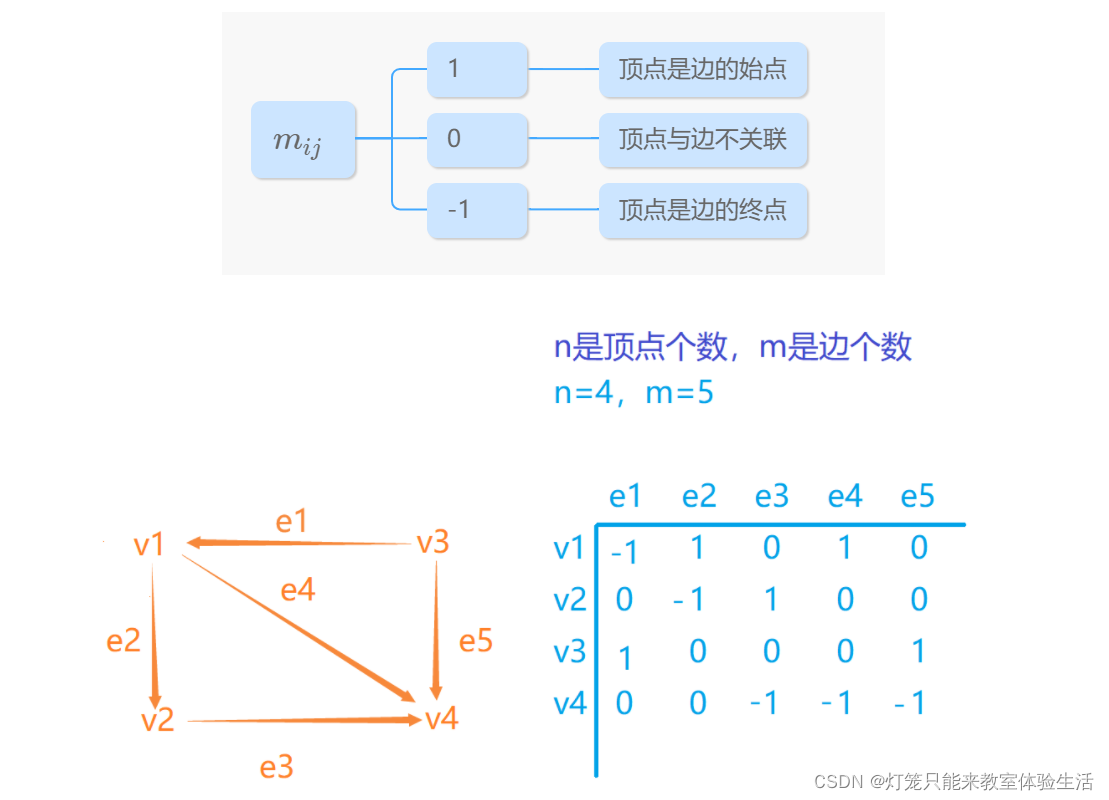
邻接矩阵

• 邻接矩阵是一个方阵，行和列都与顶点个数相同。
• 矩阵元素 a_ij 的值为 顶点i 到 顶点j 的边的条数。
• 如果是某个顶点有一个环，认为该顶点到自己的边有1条。
• 如果顶点无环，那么对角线上是0的（对角线上是自己到自己的 边的条数）

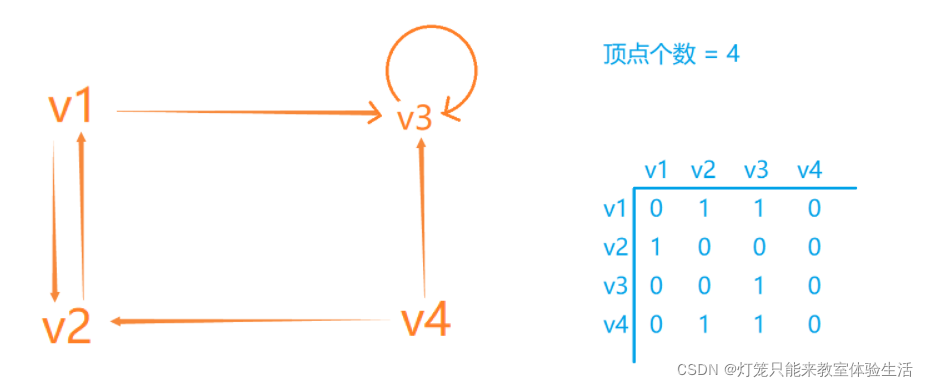
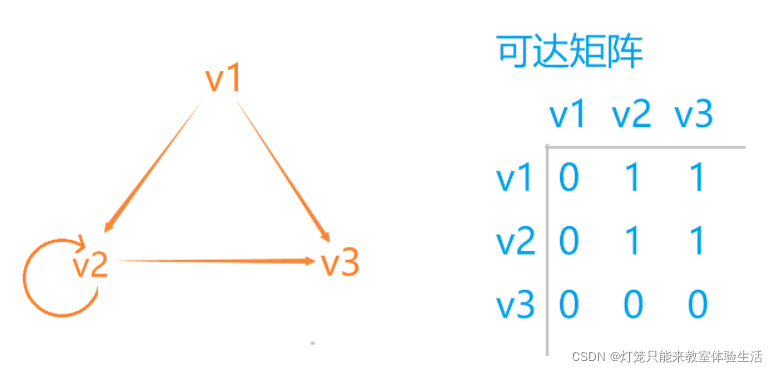
可达矩阵

• n为图的顶点数，矩阵的规模是n×n。
• 如果顶点v与顶点u之间存在通路（v可达u），那么u->v值为1。

欧拉图与哈密顿图

欧拉图

概念

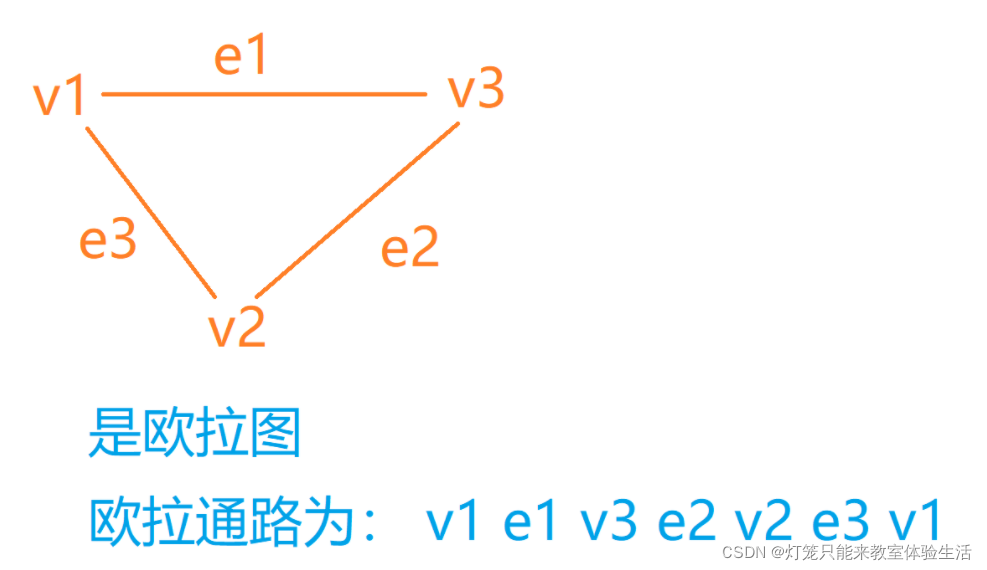
• 通过所有边一次且仅一次，并且经过所有顶点的通路称为欧拉通路。
• 若欧拉通路的始点和终点相同，称这个通路为欧拉回路。
• 具有欧拉回路的图称为欧拉图。
• 具有欧拉通路而没有欧拉回路的图称为半欧拉图。

判定定理

• 无向图G是欧拉图的充要条件：G是连通图，并且没有奇度顶点。
• 无向图G是半欧拉图的充要条件：G是连通图，并且恰有两个奇度顶点。
• 有向图D是欧拉图的充要条件是：D是强连通的（任意两个顶点可以互达），并且每个顶点的入读等于出度。
• 有向图D是半欧拉图的充要条件是：D是单向连通的，并且恰有两个奇度顶点，其中一个顶点的入度比出度大1，另一个顶点的出度比入度大1，而其余的顶点出度等于入度。
• 规定无向图是欧拉图。

哈密顿图

概念

• 经过图中所有顶点一次且仅一次的通路称为哈密顿通路。
• 经过图中所有顶点一次且仅一次的通路称为哈密顿回路。
• 具有哈密顿回路的图称为哈密顿图。
• 具有哈密顿通路而没有哈密顿回路的图称为半哈密顿图。
• 规定平凡图是哈密顿图。

判定定理

• 如果无向图G是哈密顿图，那么对于G中的任意顶点V集，均有：p(G-V)≤|V|（G删除V后的连通分支小于V中的顶点数）。

  【注意，这是一个必要条件。】

• 对于一个二部图G=<V₁,V₂,E>，|V₁|≤|V₂|，且|V₁|≥2，|V₂|≥2，那么：

  1. 若G是哈密顿图，则|V₁|=|V₂|。【必要条件】
  2. 若G是半哈密顿图，则|V₂|=|V₁|+1。【必要条件】
  3. 若|V₂|≥|V₁|+2，则G不是哈密顿图，也不是半哈密顿图。

• 一个n阶无向简单图G中的任意两个不相邻顶点u和v，均有：d(u)+d(v)≥n-1,则G中存在哈密顿通路。【充分条件】

• 一个n阶无向简单图G中的任意两个不相邻顶点u和v，均有：d(u)+d(v)≥n，则G中存在哈密顿回路。【充分条件】

• 设u和v是n阶无向简单图G中的两个不相邻的顶点，且d(u)+d(v)≥n，则G为哈密顿图的充分必要条件为：GU(u,v)为哈密顿图。

  • （u,v）为新加的边。

  • 注意只要有两个不相邻的顶点满足即可，不需要所有的不相邻顶点。

• n阶竞赛图中都有哈密顿通路。

  • 竞赛图又忘了？