一.旋轉矩陣:
(1)基本
R = rotx(pi/2)
R = roty(pi/2)
R = rotz(pi/2)
分別對X Y Z軸生成3*3的旋轉矩陣
R = rotx(30, ‘deg’)
R = roty(30, ‘deg’)
R = rotz(30, ‘deg’)
可以改變輸入的方式
(2)姿態的敘述方法:
1.Y-Z-Y歐拉角
R = rotz(a)*roty(b)*rotz(c)
eul2r(a,b,c)
旋轉矩陣反解出y-z-y歐拉角度的函數為
tr2eul(R)
2.x-y-z歐拉角
R = rotx(r)*roty(p)*rotz(y)
rpy2r(r,p,y)
旋轉矩陣反解出x-y-z歐拉角度的函數為
tr2rpy(R)
3.等效軸角坐標表示法
把坐標系b看做原坐標a按向量V方向按右手方向旋轉theta度
旋轉矩陣反解出等效軸角坐標表示的函數為
[theta,V] = tr2angvec(R)
由等效軸角坐標表示轉換為旋轉矩陣的函數
R = angvec2r(theta, V)(記得把v做單位化的處理v = v / norm(v))
4.歐拉參數法表示(4元數)
在等效軸角坐標表示法的基礎上更進一步
E1=Kx*sin(θ/2);E2=Ky*sin(θ/2);E3=Kz*sin(θ/2);E4=cos(θ/2);
求解4元數的函數為
Quaternion(R)
二.齊次變換矩陣
4*4矩陣用於描述坐標系的位置和姿態
1.平移算子
transl(x, y, z)
2.旋轉算子
trotx(pi/2);troty(pi/2);trotz(pi/2)
3.各種表示下齊次矩陣的求解
rpy2tr(roll, pitch, yaw, options) 求解x-y-z歐拉角變化對應的齊次矩陣 options:’deg’或不填
angvec2tr(theta, V)求解等效軸角坐標表示的齊次矩陣
eul2tr(phi, theta, psi, options)反解出Y-Z-Y歐拉角options:’deg’或不填
同樣可以用
tr2eul(t)反解出Y-Z-Y歐拉角
tr2rpy(t)反解出x-y-z歐拉角
[theta,vec] = tr2angvec(R);反解等效軸角坐標表示
Quaternion(R) 反解4元數表示
4.求出姿態的相關表示
trprint(T, OPTIONS)
可以表示出齊次矩陣的參數
Options為:
(1)’rpy’ ; ‘euler’ ;’angvec’ ;
改變轉換的方式為rpy,歐拉角,等效軸角坐標
(2)’radian’ ;
改變顯示的方式,和‘deg’功能相對。
5.旋轉矩陣與齊次矩陣
r2t(t),rt2tr(t)可以把旋轉矩陣t增廣為齊次矩陣
tr2rt(t),t2r(t)可以把齊次矩陣t降維旋轉矩陣
6.
可以在畫圖中顯示出齊次矩陣
7.
tranimate((P1, P2, OPTIONS)
可以顯示從P1變到p2的動畫
P1,P2可以是旋轉矩陣,齊次矩陣和4元數這幾個形式任意一個
Options::
‘fps’, fps fps的值可以改變動畫的速度(默認 10)
‘nsteps’, n n是插入的中間點個數(默認 50)
‘axis’,A 坐標系限制A=[xmin, xmax, ymin, ymax, zmin, zmax]
‘movie’,M Save frames as files in the folder M
三.一維軌跡生成:tpoly和lspb
1.五次多項式軌跡規划
典型用法
[p,pd,pdd] = tpoly(p0, p1, 50);
subplot(3,1,1); plot(p); xlabel(‘Time’); ylabel(‘p’);
subplot(3,1,2); plot(pd); xlabel(‘Time’); ylabel(‘pd’);
subplot(3,1,3); plot(pdd); xlabel(‘Time’); ylabel(‘pdd’);
也可以
[S,SD,SDD] = tpoly(S0, SF, N, SD0, SDF)
SD0為初始速度,SDF為最終速度
S0為起點位置,SF為終點位置,N為步數
2.拋物線軌跡規划
典型用法
[p,pd,pdd] = lspb(p0, p1, 50);
subplot(3,1,1); plot(p); xlabel(‘Time’); ylabel(‘p’);
subplot(3,1,2); plot(pd); xlabel(‘Time’); ylabel(‘pd’);
subplot(3,1,3); plot(pdd); xlabel(‘Time’); ylabel(‘pdd’);
也可以
[S,SD,SDD] = LSPB(S0, SF, M, V)
V為限定的最大速度
四.機械臂的構建
1.Link
Link()是構建連桿的基本函數
建立連桿的基本規則是
L = Link(DH, OPTIONS)
DH = [THETA D A ALPHA SIGMA OFFSET]
THETA D A ALPHA 為基本的DH參數
theta 關節角度
d 連桿偏移量
a 連桿長度
alpha 連桿扭角
Sigma可以設定連桿的類型0為旋轉1為伸長
offset 關節變量偏移量
qlim 關節變量范圍[min max]
Options:
‘standard’ for standard D&H parameters (default).
‘modified’ for modified D&H parameters.
‘revolute’ 旋轉關節(default)
‘prismatic’ 伸長關節
建立一個旋轉連桿
L = Link([0 1.2 0.3 pi/2]);或 L = Link([0 1.2 0.3 pi/2 0])
L = Link([0 1.2 0.3 pi/2],’revolute’)
L = Link( ‘d’, 1.2, ‘a’, 0.3, ‘alpha’, pi/2);
L = Link(‘revolute’, ‘d’, 1.2, ‘a’, 0.3, ‘alpha’, pi/2);
L = Revolute(‘d’, 1.2, ‘a’, 0.3, ‘alpha’, pi/2);
建立一個移動連桿
L = Link([0 1.2 0.3 pi/2 1])
L = Link([0 1.2 0.3 pi/2],’prismatic’)
L = Link( ‘theta’, 0, ‘a’, 0.3, ‘alpha’, pi/2);
L = Link(‘prismatic’, ‘ theta’, 0, ‘a’, 0.3, ‘alpha’, pi/2);
L = prismatic(‘ theta’, 0, ‘a’, 0.3, ‘alpha’, pi/2);
通過操作
L.theta;L.d;L.a;L. alpha 。。。。
可以顯示,修改連桿的參數
操作函數:
%A 連桿變換矩陣
% RP 關節類型: ‘R’或’P’
% friction 摩擦力
% nofriction 摩擦力忽略
% dyn 顯示動力學參數
% islimit 測試關節是否超出軟限制
% isrevolute 測試是否為旋轉關節
% isprismatic 測試是否為移動關節
% display 連桿參數以表格形式顯示
% char 轉為字符串
L.A(X)可以顯示連桿變換矩陣,但是需要補齊DH參數變量,X在旋轉連桿中就是theta 值
在伸長連桿中就是d的值。
L.RP 返回關節類型 返回R表示旋轉關節,P為伸長關節
其他的用法類似。。。
2.SerialLink
使用SerialLink可以把連桿聯系起來形成機械臂
(1)基本用法
R = SerialLink(R1, options) 復制機器人R1
R = SerialLink([L1 L2 …], OPTIONS) 機器人連接,將L2的基座連接到L1的末端.
R = SerialLink(DH, OPTIONS),矩陣DH的構成:每個關節一行,每一行為[theta d a alpha](默認為旋轉關節),第五列(sigma)為可選列,sigma=0(默認)為旋轉關節,sigma=1為移動關節
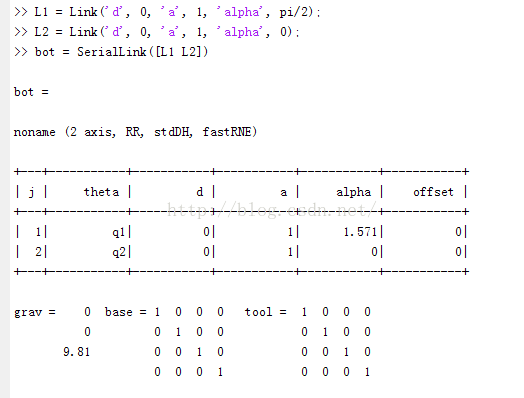
OPTIONS可以是:
‘name’、’comment’、’manufacturer’
‘base’、’tool’、’gravity’、’plotopt’
‘name’可以用於給機械臂命名
bot = SerialLink([L1 L2], ‘name’, ‘my robot’)
‘name’、’comment’、’manufacturer’的用法都差不多。用於標定一些額外信息
‘base’, ‘tool’,用於設定基坐標和工具坐標的原點
>>mdl_puma560
>>p560_2 = SerialLink(p560, ‘base’, transl(-0.5, 0.5, 0) )
(2)R.teach()可以進入一個自由調節的界面
>> p560.teach()
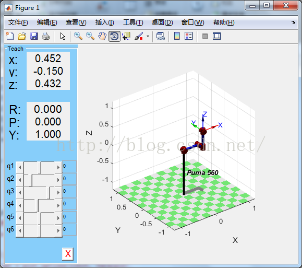
在界面中可以任意調節個關節變量
調節好需要的機械臂姿態后按×
然后p560.getpos()可以進一步得到剛調出來的各變量的值
(3)R.plot(Q, options)可以顯示出機械臂
當Q為1*N維向量,向量元素為各關節變量,顯示的是靜態的機械臂
Q為M*N矩陣,列向量元素為各關節變量,顯示一個機械臂的動圖
Options::
‘workspace’, W 為空間限制W = [xmn, xmx ymn ymx zmn zmx]
‘floorlevel’,L 底板在Z軸的顯示位置
Eg
>>mdl_puma560
>> p560.plot(q, ‘floorlevel’,0);
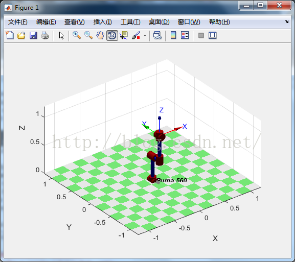
五.運動學常用函數
正運動學求解
Q = R.fkine(T)
逆運動學求解
T = R.ikine(Q, OPTIONS)
Options:: ‘deg’
Eg:
clear;
clc;
clear L
% th d a alpha
L(1) = Link([ 0 0 0 -pi/2 0]);%定義連桿
L(2) = Link([ 0 1 0 pi/2 0]);
L(3) = Link([ 0 0 0 0 1]);
L(4) = Link([ 0 0 0 -pi/2 0]);
L(5) = Link([ 0 0 0 pi/2 0]);
L(6) = Link([ 0 1 0 0 0]);
bot = SerialLink(L, ‘name’, ‘Stanford arm’);%連接連桿
T=transl(1,2,3)*trotz(60,’deg’)*troty(30,’deg’)*trotz(90,’deg’)
inverse_kinematics=bot.ikine(T,’pinv’);%逆向運動學
theta1=inverse_kinematics(1);
theta2=inverse_kinematics(2);
d3=inverse_kinematics(3);
theta4=inverse_kinematics(4);
theta5=inverse_kinematics(5);
theta6=inverse_kinematics(6);
forward_kinematics=bot.fkine([theta1 theta2 d3 theta4 theta5 theta6])%前向運動學,驗證結果的准確性.