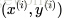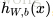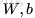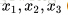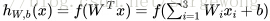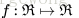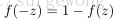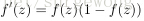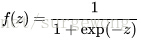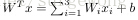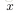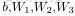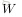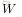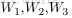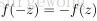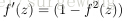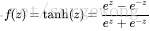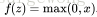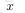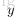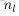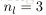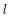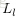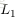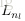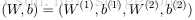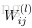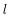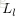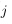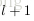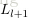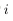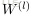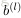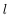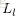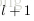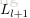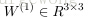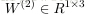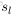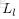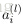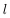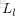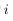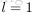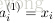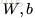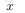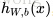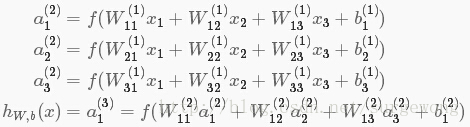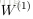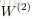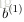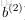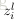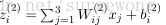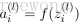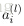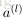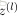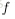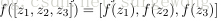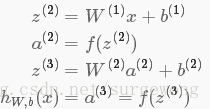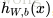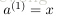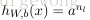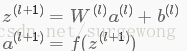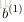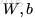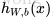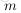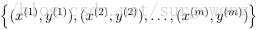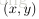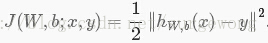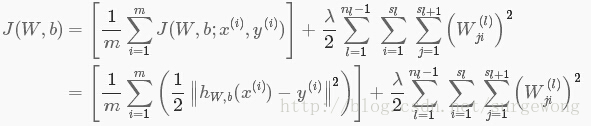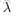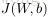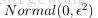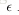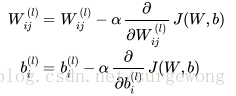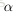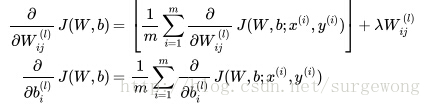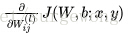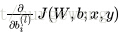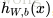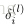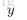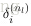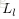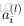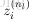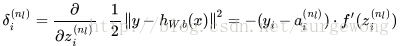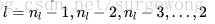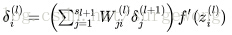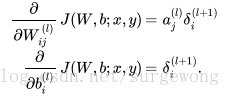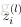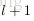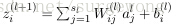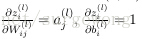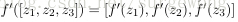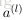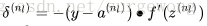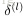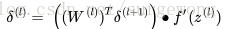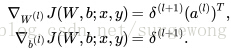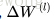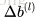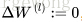Multi-Layer Neural Network
http://blog.csdn.net/surgewong
接触机器学习有一段时间了,但是对于神经网络一直感觉比较“神秘”,再加之深度学习的概念炒得这么热,都不好意思说自己不懂神经网络了。本文主要是为了记录自己对神经网络的理解以及一些心得,由于是一个新手,其中的一些理解不免有些错误,望各位能够指正。本文主要参考
UFLDL Tutorial
的同名教程【1】,在理解过程中主要参考了博客,反向传播BP算法【2】。正如【2】所说【1】中变量的上下标比较多,理解起来可能有些不便,记得耐心看下去哦。
一、初识神经网络
给出一个监督学习的问题,输入一系列的带标签的
形如
的训练数据,神经网络可以给出一个复杂的、非线性的形如
的模型,其参数为
。所有的神经网络模型基本上就是围绕这两个参数展开的。
先了解一下单个神经元(neuron)的网络。其实逻辑回归(
Logistic Regression )(不熟悉的同学可以参考【3】),就是一个单神经元网络。
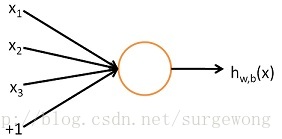
上面的“网络”结构,输入3个变量
,外加一个截距(intercept)(+1)。输出结果为:
,这里的函数
是
激励函数(activation function)
【4】,最常用的激励函数时
sigmoid函数
,采用它,那这个网络就变成了逻辑回归问题。sigmoid的函数有些很重要的特性,
和
。
刚接触神经网络不久,对一些习以为常的概念感觉有点疑惑,在这里记下自己对其的理解。上面用到公式
,可以这样理解,把1,
看成变量
的分量,变量
看成是
的分量(注意:与网络参数中的
不同,网络中参数是指
)。另外作为一个初学者,想必很想知道激励函数的作用。激励函数是对生物神经信息处理的一种模拟,根据【4】里的说法,非线性的激励函数能够使得网络系统使用较少的节点适应复杂的模型。激励函数的作用有点类似与SVM中的核函数的作用,是对网络功能的一种扩展。
sigmoid函数是最常用的激励函数,除此之外还有
双曲正切函数(hyperbolic tangent)
,不过双曲正切函数将值映射到(-1,1),相比sigmoid就相当于将类别分为-1和1,可以认为是sigmoid函数的一种“拉伸”。双曲正切函数的特性有:
,
最近的研究发现还有一种新的激励函数,
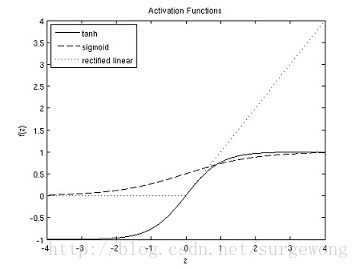
修正后的线性函数(rectified linear function)
,在小于0的部分,激励函数输出0,大于0的部分,输出为 原来的值。与sigmoid函数和双曲正切函数相比,该函数没有限定其值域,并且该函数在0点出,不可导。
下面给出的是sigmoid,tanh,修改后的线性函数的图:
二、神经网络模型(Neural Network model)
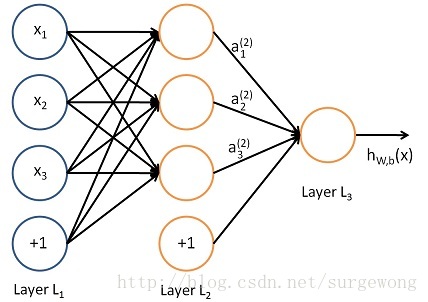
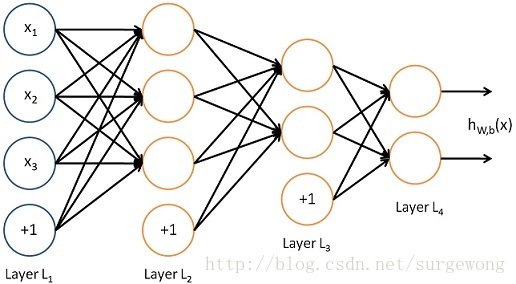
下面考虑一个简单地三层的网络结构,相比单个神经元网络结构而言只是增加了一个中间隐层(hidden layer)。隐层(hidden)是相对于输入(Input layer)和输出层(Output layer)而言的,输入层是指输入的数据
的各个分量,这个是可见的;输出层是指输出的值
的分量(如果是1维,就相当于是一个分类问题)。
上图的网络结构中+1表示一个
偏置(bias)
,也就是上面讲的截距(intercept),这个虽然是网络中的一个节点,但是在说网络结构的时候,通常不将其计算在内。上图中的网络结构可以描述成,
三个输入节点,三个隐藏节点,一个输出节点。
为了描述这个网络结构,令网络层数为
,在上述网络结构中
。将第
层表示成
,那么输入层就是
,输出层就是
。网络的参数可以表示成
,这里
表示,从第
层
的第
个节点到第
层
的第
个节点的权值,
和
就是第
层
到第
层
的网络参数。网络中给出的输入3个节点,隐层节点3个,输出节点1个,有
,
。令
为层
中节点的个数(不包括偏置节点)。
令
为第
层
的第
个节点经过激励函数之后的输出值。当
时,有
。给定
输入
,根据网络结构,可以计算出
网络输出的结果为
:
上面的公式是
的分量形式,在实际运算过程中,主要是通过矩阵和向量进行的。为了简化公式,令
为第
层的第
个节点输入的和,例如
,那么就有
。即便如此,
仍然是单个值,是向量
的分量。为此将激励函数
应用在向量上,也就是对向量的每个元素计算函数值,例如
。这样公式可以写成:
接下来就可以通过矩阵和向量的操作得到网络的输出结果
,这个过程叫着
前向传播(forward propagation)。更一般地
,令
,
,在
第
层和
第
层之间有:
上面我们给出最后的结果是1维,输出多维的结果其实是一样的,都有
,只不输出的最后一层的结果是对应的多维而已。同样对应包含更多隐层的网络结构,也是类似的,因为其每一层之间的计算的方式都是类似的(请看上面的递推公式)。还有每层的节点个数都是可以不同的,只是对应上面的递推公式中变量
的维数有所变化而已。在设计网络的过程中,可以选择不同的
网络层数
,
不同层数的节点个数
,以及最后
输出结果的维数
。它们所用的递推公式都是相同的。
三、后向传播算法(Back Propagation Algorithm)
上面介绍了前向传播(forward propagation)的过程,也就是给定网络参数
的情况下,通过网络结构计算得到最后的结果
。很自然地就想知道如何计算得到网络参数
。这里就需要介绍
后向传播算法(Back Propagation Algorithm)
,要了解这部分也可以参考【2】。
网络参数
是通过训练得到的,假定有
个元素的训练集合
,对与单个训练样本
,其代价函数(cost function)为:
对于
个元素,定义总的代价函数为:
这里引入了一个正则项,主要是为了防止过拟合,从上面的公式可以看出,正则项中没有偏置项
,根据【1】中的理解,偏置项对网络最终的结果影响不大,所以就没有考虑。(注:这里没有完全理解)正则项的系数为
,主要是为了调节两者的权重比值。
在训练过程,主要目的就是最小化自变量为
的
总代价函数
。在网络的最初始阶段,
都是未知的,需要对其进行初始化,比较常用的初始化方法是将所有值初始化为零,但是总代价函数是一个非凸函数,使用梯度下降法很容易导致求解得到局部最优解,而梯度下降法在实际网络求解过程中,效果都不错,为了避免产生局部最优解的情况,实际初始化方法一般采用正态分布
(
一般较小,例如0.01)。如果初始化为同一个值,那么相同隐层下的节点的输出值都是相同的,不利于求解,采用正态分布随机的初始化主要是为了打破对称性(symmetric breaking)。
使用梯度下降法更新
,来求解得到结果,其计算公式为:
公式中的
是学习率,简单说来就是小的增量。下面公式给出了上面两个偏导函数的求解方法:
进一步问题简化了:在单个样本
下,
,
的计算问题。这里用到就是
后向传播(Back Propagation Algorithm)算法
。算法的大致思路:在初始化的网络中,使用前向传播,计算
,然后计算每层的每个节点的误差
(其实就是偏导)
,这个值代表与“真实结果”的差。很容易通过比较
,
获取最后输出结果的
,最关键的就是计算隐层中
。后向传播算法的步骤:
1. 使用
初始化网络参数
,计算每一层
的输出每个节点的输出
,直到最后一层
2. 对于输出层(层
),计算每个节点相对于输入
的误差:
3. 对于隐层,
中的每一个节点误差
,这里是将后面一层的误差传播到前面一层,前面一层通过连接的权值将这些误差累计起来:
4. 计算得到每层的每个节点的
,就可以计算
和
了:
怎么理解上述中的两个公式呢?还记得
的定义么?为了更加容易理解,这里给出第
的求解公式
,求偏导有
,使用链式规则很容易得到上面的结果。
上面得到的结果是单个分量的形式,下面将其表达成矩阵和向量形式。将激励函数的导数应用于向量的每个元素,类似的有:
。同时用
表示向量或矩阵的元素之间的乘法,而不是矩阵运算,相当于matlab中的点乘。于是上面的反向传播算法可以表述为:
1. 使用
初始化网络参数
,计算每一层
的输
出向量
,直到最后一层
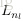
2. 对于输出层(层
),计算每层的误差向量:
3. 对于隐层,
中的层的误差向量
,
4. 计算得到每层的 误差向量,就可以计算每层参数
的梯度了:
四、算法实现
首先定义
为
的各个元素变化构成的矩阵,
为
的各个元素变化构成的矩阵。那么实现步骤如下
1. 初始化网络,
,

2. 对于
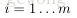
使用后向传播算法计算
和
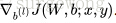
更新
,
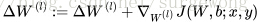
更新
,
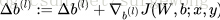
4. 最后跟新
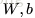
本文基本上算是对【1】的翻译和注释,现在基本上算是整理清楚了网络的结构,可以进行下一步的学习了。下面附上UFLDL教程下,matlab的实现代码。由于是MNIST手写数字是一个多分类问题,最后一层使用的损失函数和Softmax的类似,与上文中的二次损失函数不同,在代码supervised_dnn_cost.m的实现部分需要注意。另外代码可以参考【5】。
function [ cost, grad, pred_prob] = supervised_dnn_cost( theta, ei, data, labels, pred_only)
%SPNETCOSTSLAVE Slave cost function for simple phone net
% Does all the work of cost / gradient computation
% Returns cost broken into cross-entropy, weight norm, and prox reg
% components (ceCost, wCost, pCost)
%% default values
po = false;
if exist('pred_only','var')
po = pred_only;
end;
%% reshape into network
stack = params2stack(theta, ei);
numHidden = numel(ei.layer_sizes) - 1;
hAct = cell(numHidden+1, 1);
gradStack = cell(numHidden+1, 1);
% stack 记录着网络的参数W1,b1;W2,b2(这是隐层数为1的结果,多层的情况类似)
% numHidden 隐层的数目
% hAct 网络每一层的输入与输出结果(输入层除外)(为了更清楚地了解神经网络的运行过程,下面的计算过程,每层的中间结果都保存在这个节点中)
% gradStack 训练网络的梯度
%% forward prop
for l = 1:numHidden+1
if(l == 1)
hAct{l}.z = stack{l}.W*data; % 第一个隐层,将训练数据集作为其数据
else
hAct{l}.z = stack{l}.W*hAct{l-1}.a; % 第l层的输入,是第l-1层的输出,
end
hAct{l}.z = bsxfun(@plus,hAct{l}.z,stack{l}.b); % 第l层的节点的输入加上偏置
hAct{l}.a = sigmoid(hAct{l}.z); % 应用激活函数
end
% 预测概率为softmax方式,可能由于框架的原因,使用二次损失函数计算出来的效果不是很好
total_e = exp(hAct{numHidden+1}.z);
pred_prob = bsxfun(@rdivide,total_e,sum(total_e,1));
hAct{numHidden+1}.a = pred_prob;
%% return here if only predictions desired.
if po
cost = -1; ceCost = -1; wCost = -1; numCorrect = -1;
grad = [];
return;
end;
%% compute cost
% 使用softmax方法,计算J(W,b),最后一个层的输出结果就是hw,b(x) = hAct{numHidden+1}.a
label_index = sub2ind(size(hAct{numHidden+1}.a),labels',1:size(hAct{numHidden+1}.a,2));
ceCost = -sum(log(hAct{numHidden+1}.a(label_index))); % softmax 的方式计算损失函数,不带正则项
%% compute gradients using backpropagation
% 计算每层输出的误差(对输入z的偏导)
% sigmoid的导函数 f'(z) = f(z)(1-(f(z)))
% a = f(z)
tabels = zeros(size(hAct{numHidden+1}.a));
tabels(label_index) = 1;
for l = numHidden+1:-1:1
if(l == numHidden+1)
hAct{l}.delta = -(tabels - hAct{l}.a); % 输出层使用softmax的损失函数,所以和二次项损失函数不同,其他的都是一样的
else
hAct{l}.delta = (stack{l+1}.W'* hAct{l+1}.delta) .* (hAct{l}.a .*(1- hAct{l}.a));
end
if(l == 1)
gradStack{l}.W = hAct{l}.delta*data';
gradStack{l}.b = sum(hAct{l}.delta,2);
else
gradStack{l}.W = hAct{l}.delta*hAct{l-1}.a';
gradStack{l}.b = sum(hAct{l}.delta,2);
end
end
%% compute weight penalty cost and gradient for non-bias terms
wCost = 0;
for l = 1:numHidden
wCost = wCost+ sum(sum(stack{l}.W.^2)); % 网络参数W 的累计和,正则项损失
end
cost = ceCost + .5 * ei.lambda * wCost; % 带正则项的损失
% Computing the gradient of the weight decay.
for l = numHidden+1: -1 : 1
gradStack{l}.W = gradStack{l}.W + ei.lambda * stack{l}.W;
end
%% reshape gradients into vector
[grad] = stack2params(gradStack);
end
【1】UFLDL:
Multi-Layer Neural Network
【2】CSDN:
反向传播BP算法
【3】UFLDL:
Logistic Regression
【4】Wikipedia:
activation function
【5】CSDN:
ufldl学习笔记与编程作业:Multi-Layer Neural Network