博客

离散数学（8）——函数

函数（映射）

• 函数（function），映射（mapping）：
  
  单值的二元关系
  
• 单值：∀x∈domF,∀y,z∈ranF,xFy∧xFz→y=z

函数的记号

• 
  F(x)=y
  
  ⟺<x,y>∈F⟺xFy
• 
  Φ
  
  是空函数
• 常用**F,G,H,…,f,g,h,…**表示函数

偏函数

• 设F是函数
• A到B的偏函数（partial function） domF⊆A∧ranF⊆B
• A称为F的
  
  前域
  

全函数

• 全函数（total function）：domF=A
• 全函数记作 F：A→B
• A到B的全体全函数记为B
  
  ^A
  
  =A→B={F|F:A→B}
• 性质
  • 单射（injection）：F是单根的
  • 满射（surjection，onto）：ranF=B
  • 双射（bijection），
    
    一一对应
    
    （1-1 mapping）：F既是单射又是满射
  • 
    单射，满射，双射个数判断
    
    • 设|A|=n,|B|=m
    • n<m时，A→B中无满射，无双射，单射个数为m(m-1)…(m-n+1)
    • n>m时，A→B中无单射，无双射，满射个数为
      
      
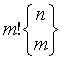
    • n=m时，A→B中双射个数为n!

象, 原象

• 设 f:A→B, A’⊆A, B’⊆B
• A’的象(image)是
  
  f(A’) = { y | ∃x( x∈A’ ∧ f(x)=y ) } ⊆ B
• B’的原象(preimage)是
  
  f
  
  ^-1
  
  (B’) = {x|∃y(y∈B’∧f(x)=y)}⊆ A

特殊函数

• 常数函数:
  
  f:A→B, ∃b∈B, ∀x∈A, f(x)=b
• 恒等函数:
  
  I
  
  _A
  
  :A→A, I
  
  _A
  
  (x)=x

特征函数

• 特征函数:
  
  χ
  
  _A
  
  :E→{0,1}, χ
  
  _A
  
  (x)=1⟺x∈A
• 当 Φ⊂A⊂E时, χ
  
  _A
  
  是满射

单调函数

• 设f:A→B, <A,≤
  
  _A
  
  >, <B,≤
  
  _B
  
  >是偏序集
• 单调增:
  
  ∀x,y∈A, x≤
  
  _A
  
  y⇒f(x)≤
  
  _B
  
  f(y)
• 单调减:
  
  ∀x,y∈A, x≤
  
  _A
  
  y⇒f(y)≤
  
  _B
  
  f(x)
• 严格单调: 把≤换成<, 是单射

自然映射

• 设R为A上等价关系
• 自然映射, 典型映射:
  
  f:A→A/R, f(x)=[x]
  
  _R
  
• 当R=I
  
  _A
  
  时, f是单射

定理

• 设 g:A→B, f:B→C, fog:A→C,则
  
  (1) 若 f,g 均为满射, 则 fog 也是满射.
  
  (2) 若 f,g 均为单射, 则 fog 也是单射.
  
  (3) 若 f,g 均为双射, 则 fog 也是双射.
• 设 g:A→B, f:B→C, 则
  
  (1) 若 fog 为满射, 则 f 是满射.
  
  (2) 若 fog 为单射, 则 g 是单射.
  
  (3) 若 fog 为双射, 则 g 是单射, f 是满射.

反函数

• 设 f:A→B，且f为双射，则
  
  f
  
  ^-1
  
  :B→A，且f
  
  ^-1
  
  也为双射.
• 若 f: A→B 为双射，则 f
  
  ^-1
  
  : B→A 称为 f 的反函数

单边逆

• 设f:A→B, g:B→A

  左逆:
  
  g是f的左逆 ⟺ gof=I
  
  _A
  

  右逆:
  
  g是f的右逆 ⟺ fog=I
  
  _B
  

• 定理

  设 f:A→B, 且A≠∅, 则
  
  (1) f 存在左逆 ⟺ f 是单射;
  
  (2) f 存在右逆 ⟺ f 是满射;
  
  (3) f 存在左逆, 右逆 ⟺ f 是双射 ⟺ f 的左逆和右逆相等