注:子数组或者子字符串求解问题一般基本是用DP算法
最长回文子串的解释:正着读和反着读是一样的。
题目解析:
解法一:动态规划
从回文子串的定义我们可以得出两个结论:
(1)如果说一个子字符串是回文子串,那么给这个子字符串两边分别加一个数,如果这2个数相等,那么这个新的子字符串也是回文子串。
(2)回文子串的开始和结束位置的字符一定是相等的。
我们可以用i来表示一个子字符串的起始位置,j来表示一个子字符串的结束位置,用一个二维数组来存储i和j之间的子字符串是否是回文子串。看到这可以看出这个问题和背包问题很像。
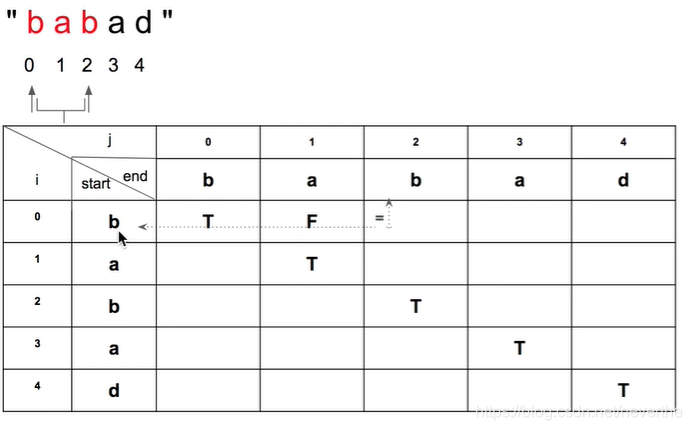
根据刚才分析得出的结论我们可知:
dp[i][j] = dp[i+1][j-1] && i和j位置的值是否相等
注:dp[i][j]表示以i开头,以j结尾的子字符串是否是回文子串。
那么我们从哪里进入动规入口呢,很明显我们可以知道:当i和j的位置是同一个时,也就是单个字符时,肯定是一个回文子串。
因此我们可以现在表中斜对角的地方都先写上T(True),然后进行递推。这里有一个问题,我们的递推顺序(也就是扫描顺序)是怎么样子的?
首先我们来下面这种扫描方法
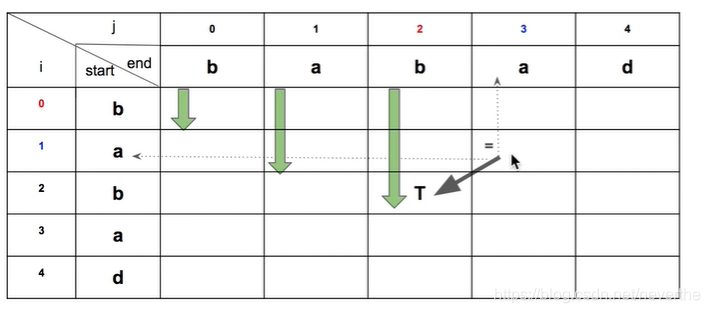
很明显,这种扫描方法是错误的,因为我们要确定一个子字符串是否是回文子串,我们必须先知道它中间的子字符串是否是回文子串【也就是我们必须先知道表中当前位置(i,j)的斜下方位置(i+1,j-1)的值】。但是现在这种扫描方法在要计算 dp[i][j]的值时,并不知道此时 dp[i+1][j-1]的值,所以不能这样扫描
正确的扫描方法有如下两种(任选其一进行扫描即可
):

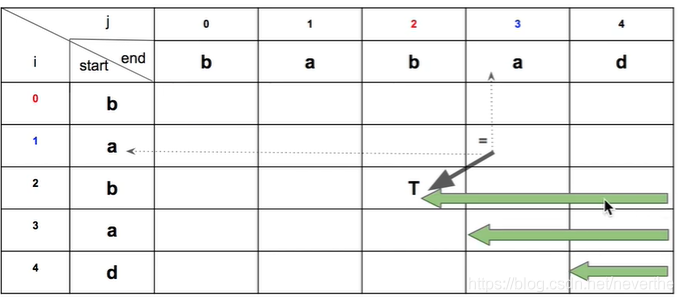
在判断子字符串是否时回文子串的同时,我们应该设置一个变量去记录时回文子串的子字符串的长度,并且不断的用更大的值去更新当前长度。
动态规划代码如下:
注:在写递推代码时,回文子串长度为2和1时无法用状态转移方程得出,因此需做特殊处理。
class Solution {
public:
string longestPalindrome(string s) {
int size = s.size();
if (size <=1 ) return s; //边界条件处理
int len=1; //记录回文子串的长度,回文子串的最小长度为1。
int start=0; // 回文子串的开始位置
int end;
vector<vector<int>>dp (size,vector<int>(size,0));
for(int i = 0;i<size;i++) dp[i][i]=1; //设置表格中对角线位置的值
for (int j = 1; j<size;j++) //i是开始位置,j是结束位置
{
for (int i=0;i<j;i++)
{
if (s[i] == s[j])
{
if (j-i<3)
dp[i][j] = 1; //特殊情况处理
else
dp[i][j] = dp[i+1][j-1];
}
if ( dp[i][j] ) //更新长度
{
if(j-i+1 > len)
{
len = j-i+1;
start = i;
}
}
}
}
return s.substr(start,len);
}
};
解法二:中心扩展法
待续……
参考:https://www.bilibili.com/video/BV1SE411y7RW?from=search&seid=2950817619903450615