推荐算法－NFM

FM对于特征的组合仅限于二阶，缺少对特征之间深层次关系的抽取。因此，NFM提出来就是在FM的基础上引入神经网络，实现对特征的深层次抽取。NFM的模型结构图如下所示：



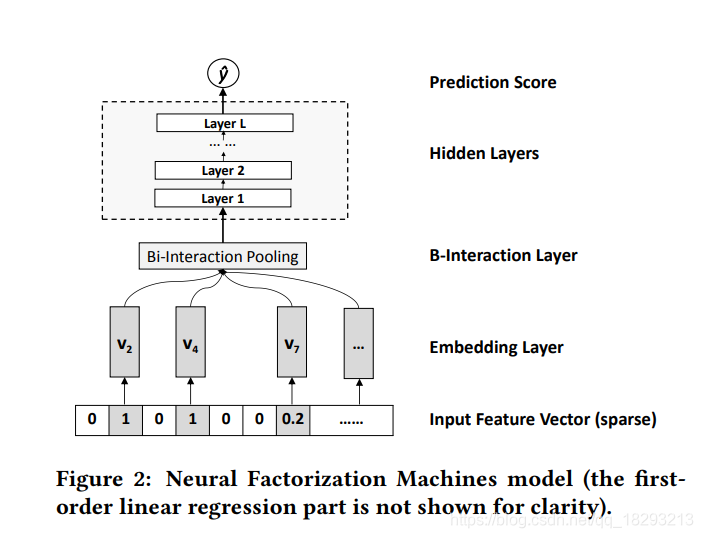
模型的结构如上图所示，首先输入就是离散化的特征，然后再进行embedding操作，获得每一个特征的向量表示。接着就到了Bi-interaction Pooling层，这里其实就是FM部分。FM的公式如下图所示：



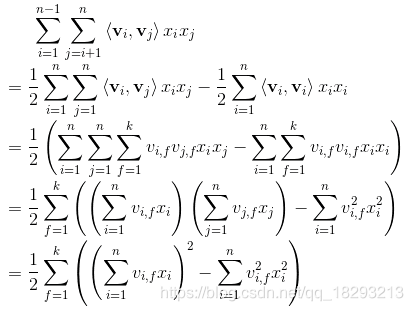
去掉最外层的累加号，我们得到的是一个长度为K的向量，也就是embedding部分的长度。然后再对这个向量送入几层全连接层即可，最后输出ctr预估值。这就是NFM的整体思路。

代码实现

权重构建，就是初始化一下embedding部分的数据，以及全连接部分的权重。然后就可以实现计算图了。

权重部分如下：

    def _initWeights(self):

        weights = dict()
        # embedding
        weights['feature_embedding'] = tf.Variable(tf.random_normal(shape=[self.featureSize, self.embeddingSize],
                                                                    mean=0.0, stddev=0.001), name='feature_embedding')
        weights['feature_bias'] = tf.Variable(tf.random_normal(shape=[self.featureSize, 1], mean=0.0, stddev=0.001), name='feature_embedding')
        weights['bias'] = tf.Variable(tf.random_normal(shape=[1]), name='bias')

        # deep

        weights['layers_{}'.format(0)] = tf.Variable(tf.random_normal(shape=[self.embeddingSize, self.deepLayers[0]],
                                                                      mean=0, stddev=0.001), name='layers_{}'.format(0))
        weights['bias_{}'.format(0)] = tf.Variable(tf.random_normal(shape=[1, self.deepLayers[0]]), name='bias_{}'.format(0))

        for i in range(1, len(self.deepLayers)):
            weights['layers_{}'.format(i)] = tf.Variable(tf.random_normal(shape=[self.deepLayers[i-1], self.deepLayers[i]],
                                                                          mean=0.0, stddev=0.001), name='bias_{}'.format(i))
            weights['bias_{}'.format(i)] = tf.Variable(tf.random_normal(shape=[1, self.deepLayers[i]]), name='bias_{}'.format(i))

        weights['layers_output'] = tf.Variable(tf.random_normal(shape=[self.deepLayers[-1], 1], mean=0.0, stddev=0.001),
                                               name='layers_output')
        weights['bias_output'] = tf.Variable(tf.random_normal(shape=[1]), name='bias_output')

        return weights

计算图部分：

    def _initGraph(self):
        self.weights = self._initWeights()

        self.featureIndex = tf.placeholder(shape=[None, None], dtype=tf.int32)
        self.featureValue = tf.placeholder(shape=[None, None], dtype=tf.float32)
        self.label = tf.placeholder(shape=[None, 1], dtype=tf.float32)
        self.dropoutKeepDeep = tf.placeholder(tf.float32, shape=[None], name='dropout_deep_deep')
        self.trainPhase = tf.placeholder(tf.bool, name='train_phase')

        # embedding
        self.embedding = tf.nn.embedding_lookup(self.weights['feature_embedding'], self.featureIndex)
        featureValue = tf.reshape(self.featureValue, shape=[-1, self.fieldSize, 1])
        self.embedding = tf.multiply(self.embedding, featureValue)  # none fieldSize embeddingSize

        # 一次项
        self.yFirstOrder = tf.nn.embedding_lookup(self.weights['feature_bias'], self.featureIndex)
        self.yFirstOrder = tf.reduce_sum(tf.multiply(self.yFirstOrder, featureValue), 2)

        # square->sum
        self.squaredSum = tf.reduce_sum(tf.square(self.embedding), 1)

        # sum->square
        self.sumedSquare = tf.square(tf.reduce_sum(self.embedding, 1))

        self.ySecondOrder = 0.5 * tf.subtract(self.sumedSquare, self.squaredSum)

        # deep

        self.yDeep = self.ySecondOrder
        for i in range(0, len(self.deepLayers)):
            self.yDeep = tf.matmul(self.yDeep, self.weights['layers_{}'.format(i)]) + self.weights['bias_{}'.format(i)]
            self.yDeep = self.deepLayerActivation(self.yDeep)
            self.yDeep = tf.nn.dropout(self.yDeep, self.dropoutDeep[i + 1])

        # bias
        # self.y_bias = self.weights['bias'] * tf.ones_like(self.label)

        # out
        self.out = tf.add_n([tf.reduce_sum(self.yFirstOrder, axis=1, keep_dims=True),
                             tf.reduce_sum(self.yDeep, axis=1, keep_dims=True)])

OK，NFM就简单介绍这些。思路相比与前面几篇比较简单，实现相对容易一些。

参考

https://www.comp.nus.edu.sg/~xiangnan/papers/sigir17-nfm.pdf



https://www.jianshu.com/p/4e65723ee632