对于 CNN 卷积网络的理解——Padding 的两种方式
导言
最近在看卷积神经网络(CNN)的时候,遇到了 padding 这个属性(补全方式),查了很多资料,发现目前网上讨论的大都是padding之后输出张量大小如何计算的问题。但对于像下面的问题却没有做出清晰的解释:
问题:当 padding=‘SAME’ 时,对于 5×5 大小的矩阵,使用 2×2 大小的卷积核,请问是如何在原输入矩阵周围补充的?那如果使用 4×4 大小的卷积核,又如何补充呢?
下面将对于 padding 这一概念从不同卷积方式的角度进行理解,而不采用原有补全的概念。希望能使得我们对这一概念有深入的理解,能对我们后面的研究工作有所帮助。
下面第一小节、第二小节主要对两种 Padding 方式 用动图 gif 刻画其如何进行卷积。第三小节对两种 Padding 方式进行了总结。
1. Padding=‘VALID’
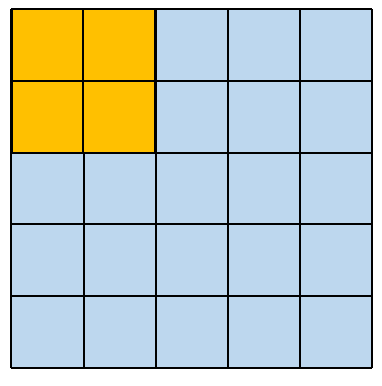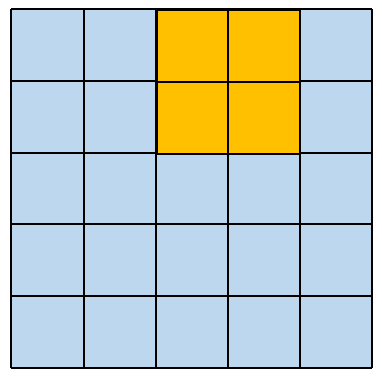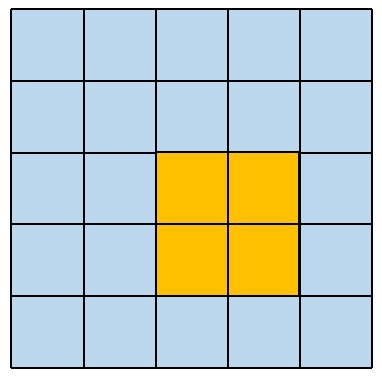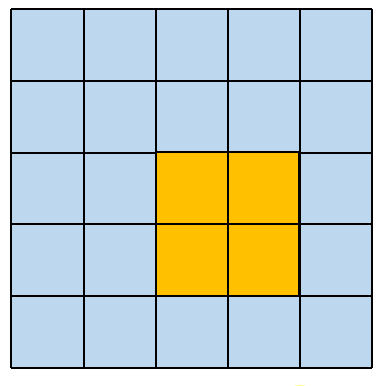
这种卷积方式很简单,这里仅仅对 5×5 大小的矩阵,使用 2×2 大小的卷积核进行举例说明。这种卷积方式保持卷积核和原矩阵最大重叠,从左边平移到右边,从上面平移到下面。
import tensorflow as tf
input = tf.Variable(tf.random.normal([1,5,5,1]))
conv = tf.keras.layers.Conv2D(1,2,padding='VALID')(input)
其对应的卷积操作如下图所示:
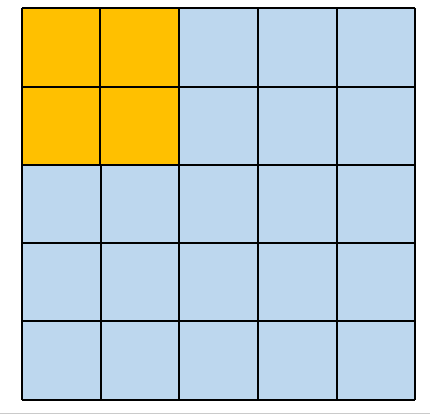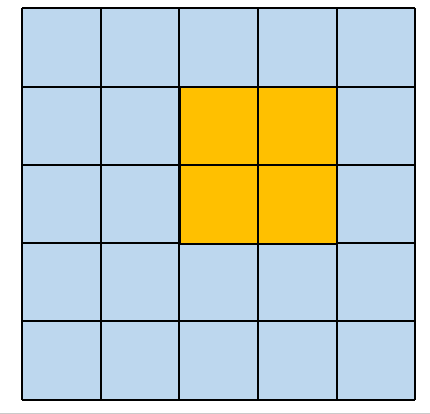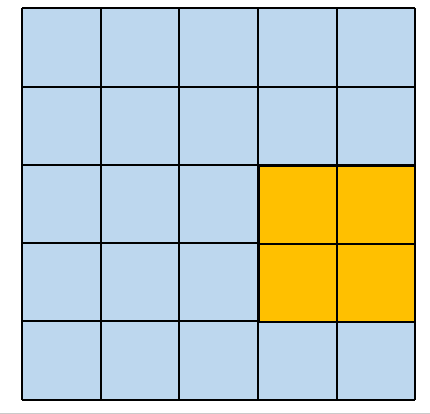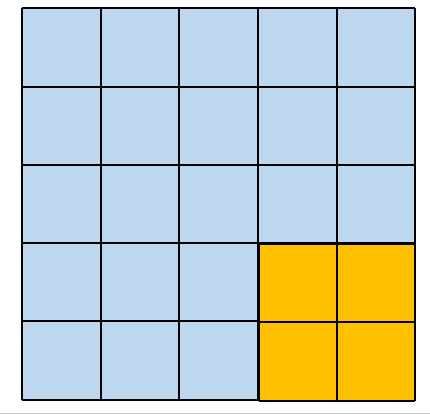
2. Padding=‘SAME’
下面便进入本文的重点第二种 padding 方式。
这种卷积方式也很简单,就是将卷积核的中心 与 原矩阵对齐。对于 3×3、5×5 这样的卷积核来说,卷积核中心就是中间的一个小方块。但对于2×2、4×4 这样的卷积核来说,卷积核中心是四个小方块,通常在 TensorFlow 中选择四个小方块中左上角的一个小方块作为标准。
下面分别列举了,对 5×5 矩阵使用 2×2 、3×3、4×4 的卷积核时所进行的卷积操作。
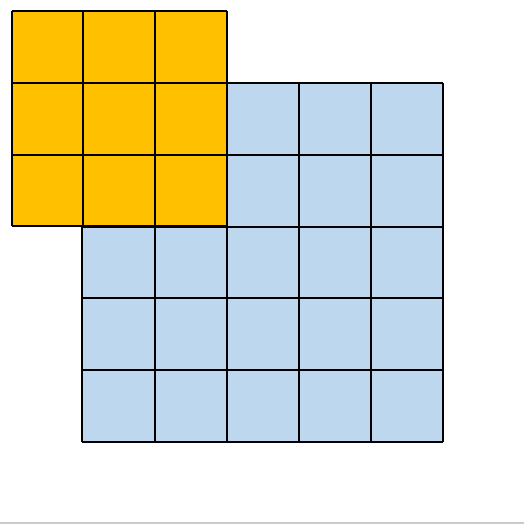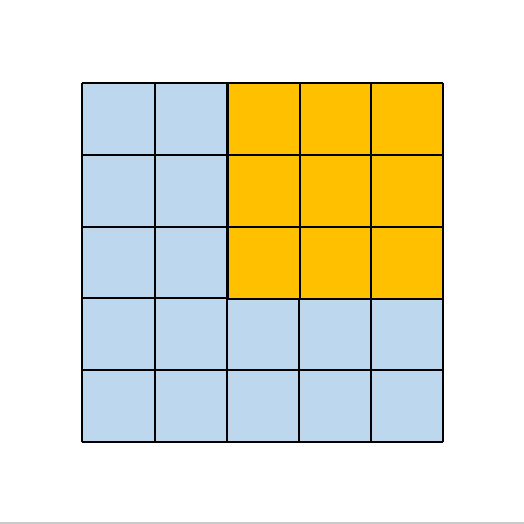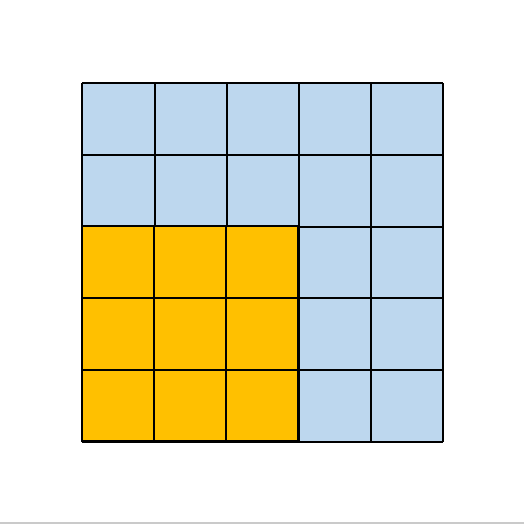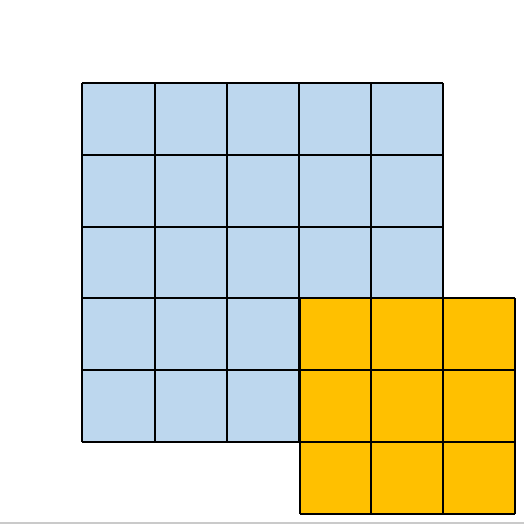
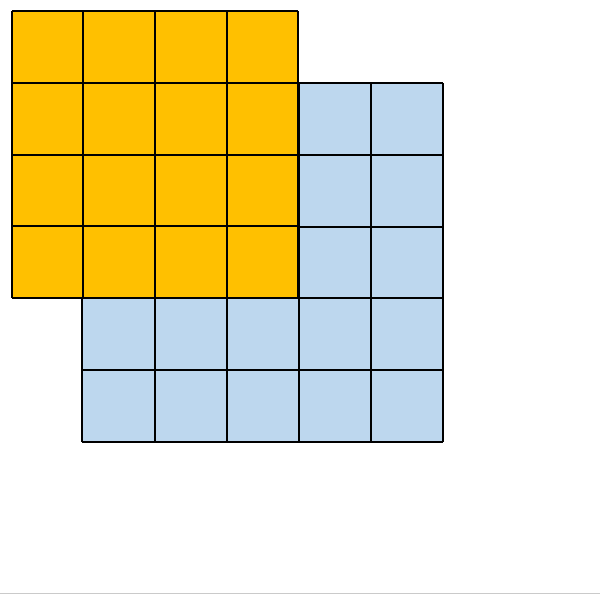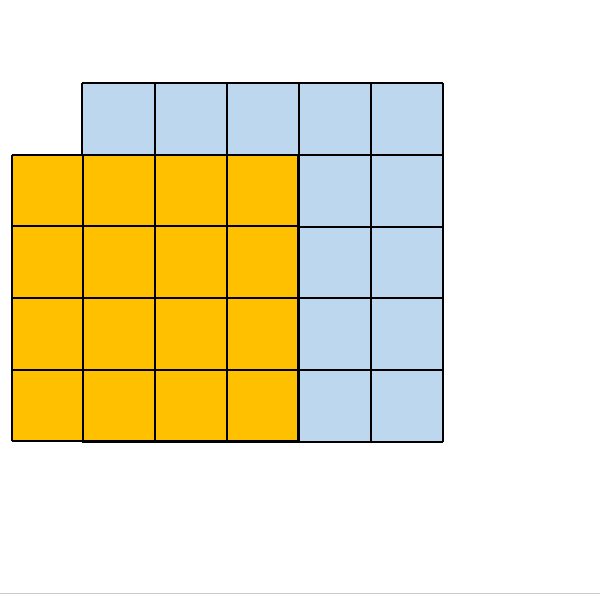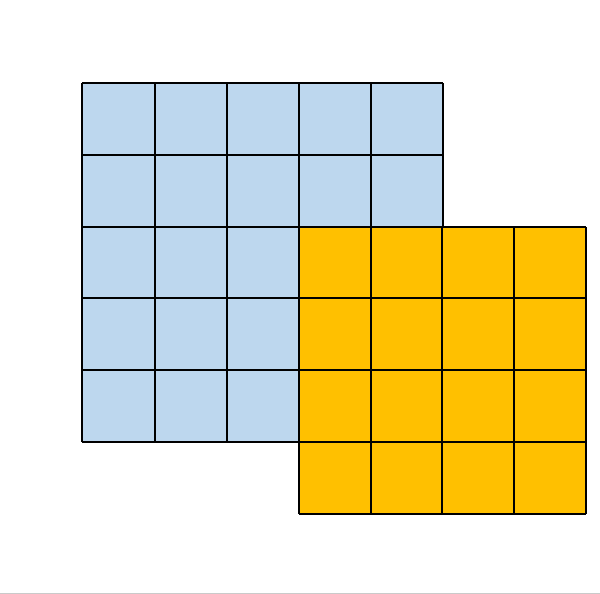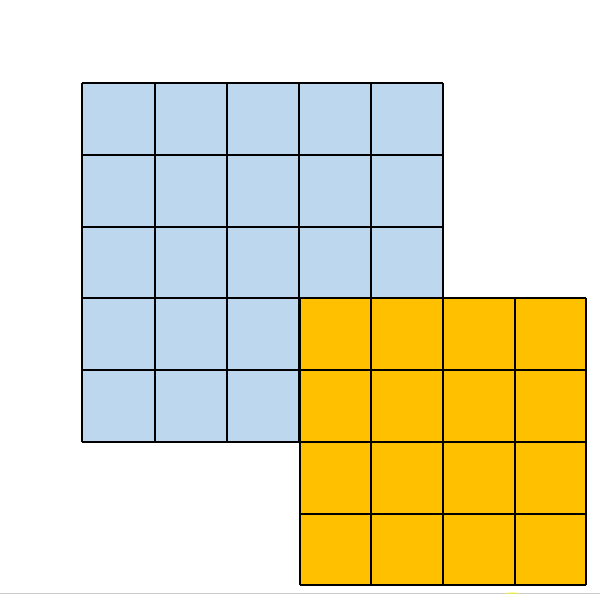
2.1. 2×2 大小的卷积核
import tensorflow as tf
input = tf.Variable(tf.random.normal([1,5,5,1]))
conv = tf.keras.layers.Conv2D(1,2,padding='SAME')(input)
其所对应的卷积操作如下所示
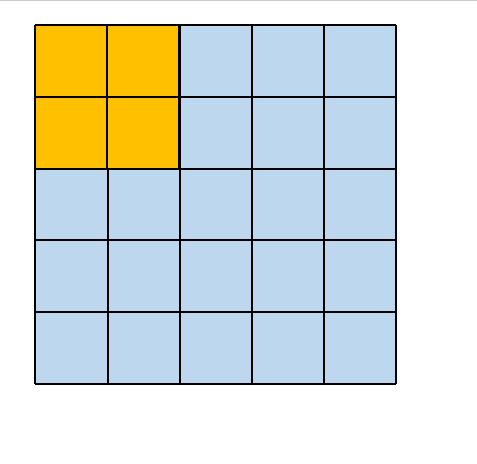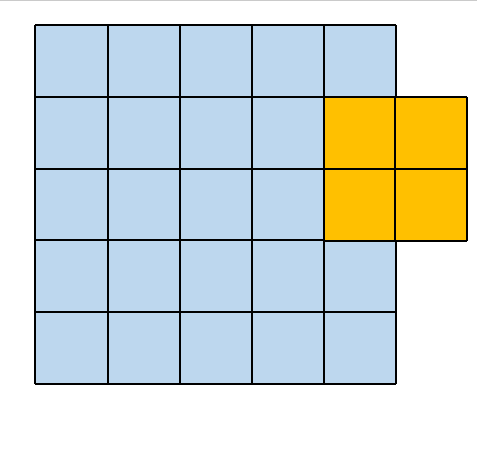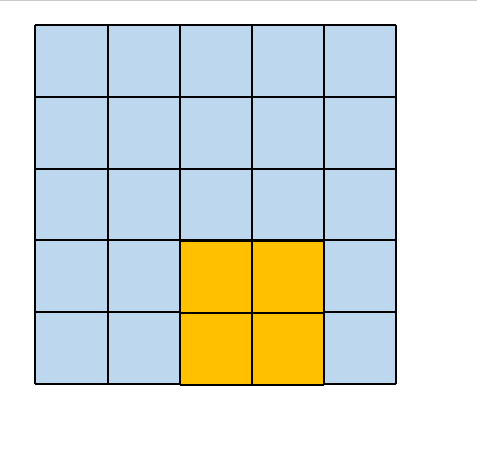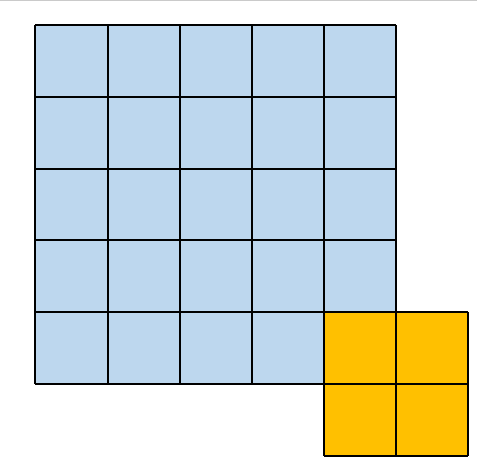
2.2. 3×3 大小的卷积核
import tensorflow as tf
input = tf.Variable(tf.random.normal([1,5,5,1]))
conv = tf.keras.layers.Conv2D(1,3,padding='SAME')(input)
其所对应的卷积操作如下所示
2.3. 4×4 大小的卷积核
import tensorflow as tf
input = tf.Variable(tf.random.normal([1,5,5,1]))
conv = tf.keras.layers.Conv2D(1,4,padding='SAME')(input)
其所对应的卷积操作如下所示
3. 对齐方式不同
其实从上面的几个例子我们可以看出,两种不同的 padding 只不过是 卷积核 与 原矩阵的对齐方式不同。
1.对于 padding=‘VALID’ 来说,要求卷积矩阵和原矩阵最大重叠,只能在原矩阵内部移动。
2.对于 padding=‘SAME’ 来说,卷积核使用卷积核中心的一个小方格与原矩阵对齐。对于大小为偶数的卷积核,中心的对齐小方格定义为中间4个小方格左上角的一个小方格。
对于卷积核移动到原矩阵外面的部分使用 0 进行填充。
(用语言确实不好描述,大家看图理解吧)
A. Strides=(2,2)
上面讨论的情况都是步进大小为 1 的情况,当步进大小大于 1 时,常常会出现一个问题:
原矩阵大小并非步进大小的整数倍。
对于最后一点余下的边界,TensorFlow 一般选择去掉最后一点无法凑整的边界。
import tensorflow as tf
input = tf.Variable(tf.random.normal([1,5,5,1]))
conv = tf.keras.layers.Conv2D(1,2,padding='VALID',strides=(2,2))(input)
其所对应的卷积操作如下所示