PID 算法原理（位置型 PID、增量型 PID 、积分分离、抗积分饱和的 PID 控制算法 C 语言实现）

一 PID 算法原理

在工业应用中 PID 及其衍生算法是应用最广泛的算法之一，是当之无愧的万
能算法，如果能够熟练掌握 PID 算法的设计与实现过程，对于一般的研发人员来
讲，应该是足够应对一般研发问题了，而难能可贵的是，在我所接触的控制算法
当中，PID 控制算法又是最简单，最能体现反馈思想的控制算法，可谓经典中的
经典。经典的未必是复杂的，经典的东西常常是简单的，而且是最简单的，想想
牛顿的力学三大定律吧，想想爱因斯坦的质能方程吧，何等的简单！简单的不是
原始的，简单的也不是落后的，简单到了美的程度。先看看 PID 算法的一般形式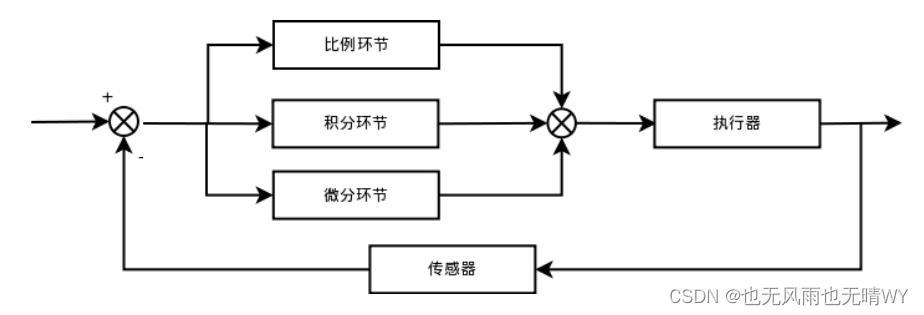：在这里插入图片描述
PID 的流程简单到了不能再简单的程度，通过误差信号控制被控量，而控制
器本身就是比例、积分、微分三个环节的加和。这里我们规定（在 t 时刻）：

1.输入量为 rin(t);
2.输出量为 rout(t);
3.偏差量为 err(t)=rin(t)-rout(t);

pid 的控制规律为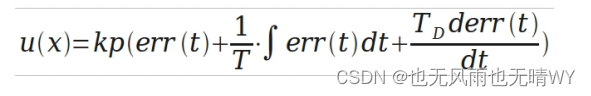 在这里插入图片描述
理解一下这个公式，主要从下面几个问题着手，为了便于理解，把控制环境
具体一下：

1.规定这个流程是用来为直流电机调速的;
2.输入量 rin(t)为电机转速预定值;
3.输出量 rout(t)为电机转速实际值;
4.执行器为直流电机;
5.传感器为光电码盘，假设码盘为 10 线;
6.直流电机采用 PWM 调速 转速用单位 转/min 表示;

不难看出以下结论：

1.输入量 rin（t）为电机转速预定值（转/min）;
2. 输出量 rout(t)为电机转速实际值（转/min）;
3.偏差量为预定值和实际值之差（转/min）;

那么以下几个问题需要弄清楚：

1.通过 PID 环节之后的 U(t)是什么值呢？
2.控制执行器（直流电机）转动转速应该为电压值（也就是 PWM 占空比）。
3.那么 U(t)与 PWM 之间存在怎样的联系呢？

二 PID 算法的离散化

上一节论述了 PID 算法的基本形式，并对其控制过程的实现有了一个
简要的说明，通过上一节的总结，基本已经可以明白 PID 控制的过程。这一节中
先继续上一节内容补充说明一下。

1.说明一下反馈控制的原理，通过上一节的框图不难看出，PID 控制其实是
对偏差的控制过程;
2.如果偏差为 0,则比例环节不起作用，只有存在偏差时，比例环节才起作用。
3.积分环节主要是用来消除静差，所谓静差，就是系统稳定后输出值和设定
值之间的差值，积分环节实际上就是偏差累计的过程，把累计的误差加到原有系
统上以抵消系统造成的静差。
4.而微分信号则反应了偏差信号的变化规律，或者说是变化趋势，根据偏差
信号的变化趋势来进行超前调节，从而增加了系统的快速性。

好了，关于 PID 的基本说明就补充到这里，下面将对 PID 连续系统离散化，
从而方便在处理器上实现。下面把连续状态的公式再贴一下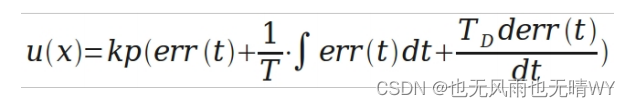：在这里插入图片描述
假设采样间隔为 T，则在第 K T 时刻：

偏差 err(K)=rin(K)-rout(K);
积分环节用加和的形式表示，即 err(K)+err(K+1)+……;
微分环节用斜率的形式表示，即[err(K)-err(K-1)]/T;
从而形成如下 PID 离散表示形式：

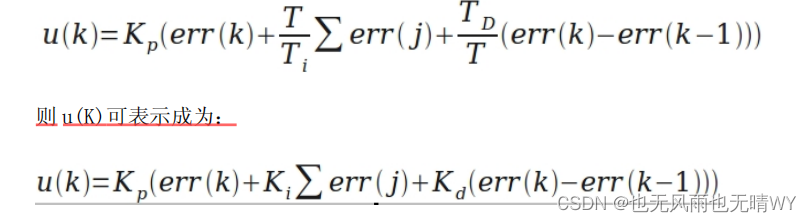
在这里插入图片描述
至于说 Kp、Ki、Kd 三个参数的具体表达式，我想可以轻松的推出了，这里节省
时间，不再详细表示了。
其实到这里为止，PID 的基本离散表示形式已经出来了。目前的这种表述形式属
于位置型 PID，另外一种表述方式为增量式 PID，由 U 上述表达式可以轻易得到：
在这里插入图片描述
这就是离散化 PID 的增量式表示方式，由公式可以看出，增量式的表达结果和最
近三次的偏差有关，这样就大大提高了系统的稳定性。
需要注意的是最终的输出。
结果应该为：

u(K)+增量调节值;
PID 的离散化过程基本思路就是这样，下面是将离散化的公式转换成为 C 语言，
从而实现微控制器的控制作用。

三位置型 PID 的 C 语言实现

上一节中已经抽象出了位置性 PID 和增量型 PID 的数学表达式，这一节，重
点讲解 C 语言代码的实现过程，算法的 C 语言实现过程具有一般性，通过 PID
算法的 C 语言实现，可以以此类推，设计其它算法的 C 语言实现。

第一步：定义 PID 变量结构体，代码如下：

struct _pid{
float SetSpeed; //定义设定值
float ActualSpeed; //定义实际值
float err; //定义偏差值
float err_last; //定义上一个偏差值
float Kp,Ki,Kd; //定义比例、积分、微分系数
float voltage; //定义电压值（控制执行器的变量）
float integral; //定义积分值
}pid;

控制算法中所需要用到的参数在一个结构体中统一定义，方便后面的使用。
第二部：初始化变量，代码如下：

void PID_init(){
printf("PID_init begin \n");
pid.SetSpeed=0.0;
pid.ActualSpeed=0.0;
pid.err=0.0;
pid.err_last=0.0;
pid.voltage=0.0;
pid.integral=0.0;
pid.Kp=0.2;
pid.Ki=0.015;
pid.Kd=0.2;
printf("PID_init end \n");
}

统一初始化变量，尤其是 Kp,Ki,Kd 三个参数，调试过程当中，对于要求的控制
效果，可以通过调节这三个量直接进行调节。
第三步：编写控制算法，代码如下：

float PID_realize(float speed){
pid.SetSpeed=speed;
pid.err=pid.SetSpeed-pid.ActualSpeed;
pid.integral+=pid.err;
pid.voltage=pid.Kp*pid.err+pid.Ki*pid.integral+pid.Kd*(pid.err-pi
d.err_last);
pid.err_last=pid.err;
pid.ActualSpeed=pid.voltage*1.0;
return pid.ActualSpeed;
}

注意：这里用了最基本的算法实现形式，没有考虑死区问题，没有设定上下限，
只是对公式的一种直接的实现，后面的介绍当中还会逐渐的对此改进。
到此为止，PID 的基本实现部分就初步完成了。下面是测试代码：

int main(){
printf("System begin \n");
PID_init();
int count=0;
while(count<1000)
{
float speed=PID_realize(200.0);
printf("%f\n",speed);
count++;
}
return 0;
}

下面是经过 1000 次的调节后输出的 1000 个数据（具体的参数整定过程就不说明
了，网上这种说明非常多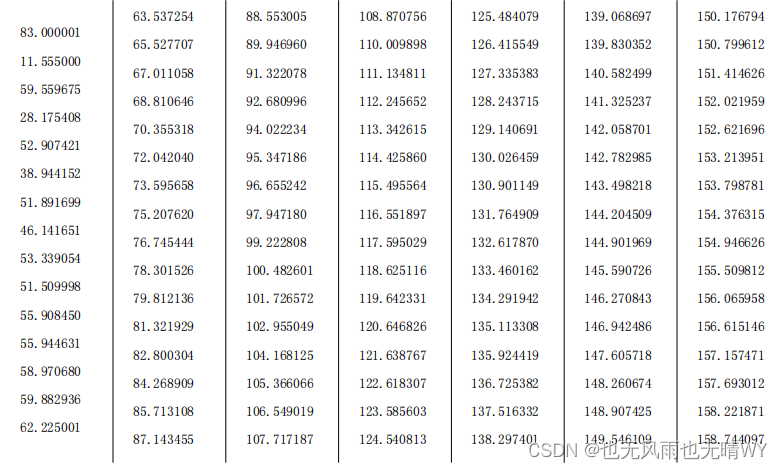）：在这里插入图片描述

四增量型 PID 的 C 语言实现

上一节中介绍了最简单的位置型 PID 的实现手段，这一节主要讲解增量式 PID
的实现方法。实现过程仍然是分为定义变量、初始化变量、实现
控制算法函数、算法测试四个部分，这里直接给出代码了。

#include<stdio.h>
#include<stdlib.h>
struct _pid{
float SetSpeed; //定义设定值
float ActualSpeed; //定义实际值
float err; //定义偏差值
float err_next; //定义上一个偏差值
float err_last; //定义最上前的偏差值
float Kp,Ki,Kd; //定义比例、积分、微分系数
}pid;
void PID_init(){
pid.SetSpeed=0.0;
pid.ActualSpeed=0.0;
pid.err=0.0;
pid.err_last=0.0;
pid.err_next=0.0;
pid.Kp=0.2;
pid.Ki=0.015;
pid.Kd=0.2;
}
float PID_realize(float speed){
pid.SetSpeed=speed;
pid.err=pid.SetSpeed-pid.ActualSpeed;
float
incrementSpeed=pid.Kp*(pid.err-pid.err_next)+pid.Ki*pid.err+pid.Kd*(p
id.err-2*pid.err_next+pid.err_last);
pid.ActualSpeed+=incrementSpeed;
pid.err_last=pid.err_next;
pid.err_next=pid.err;
return pid.ActualSpeed;
}
int main(){
PID_init();
int count=0;
while(count<1000)
{
float speed=PID_realize(200.0);
printf("%f\n",speed);
count++;
}
return 0;
}

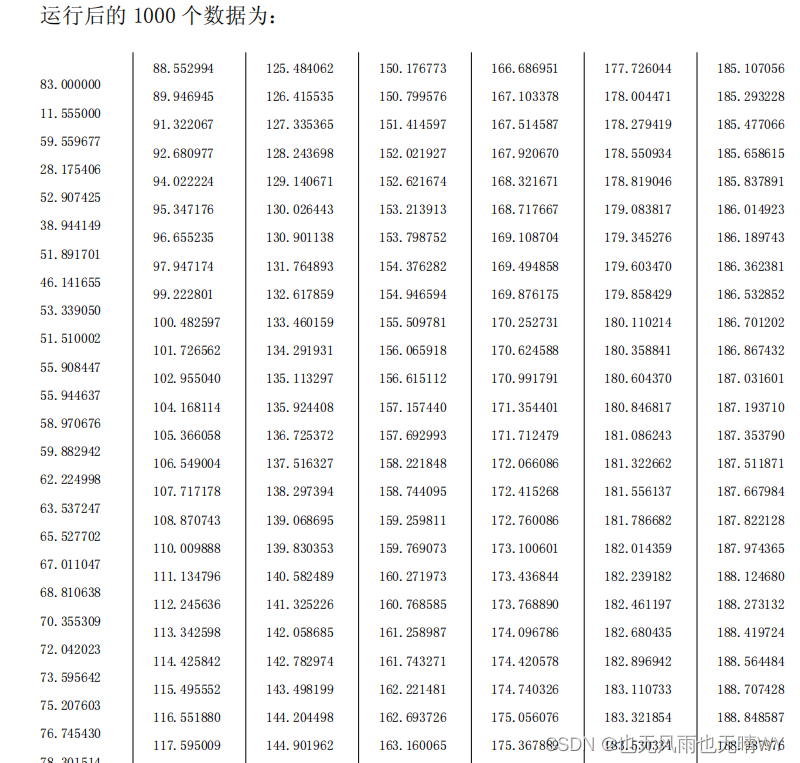
在这里插入图片描述

五积分分离的 PID 控制算法 C 语言实现

通过前面基本上已经弄清楚了 PID 控制算法的最常规的表达方
法。在普通 PID 控制中，引入积分环节的目的，主要是为了消除静差，提高控制
精度。但是在启动、结束或大幅度增减设定时，短时间内系统输出有很大的偏差，
会造成 PID 运算的积分积累，导致控制量超过执行机构可能允许的最大动作范围
对应极限控制量，从而引起较大的超调，甚至是震荡，这是绝对不允许的。
为了克服这一问题，引入了积分分离的概念，其基本思路是当被控量与设定
值偏差较大时，取消积分作用; 当被控量接近给定值时，引入积分控制，以消除
静差，提高精度。其具体实现代码如下：

pid.Kp=0.2;
pid.Ki=0.04;
pid.Kd=0.2; //初始化过程
if(abs(pid.err)>200)
{
index=0;
}else{
index=1;
pid.integral+=pid.err;
}
pid.voltage=pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*(pid.
err-pid.err_last); //算法具体实现过程

同样采集 1000 个量，会发现，系统到 199 所有的时间是原来时间的 1/2,系统的快
速性得到了提高。
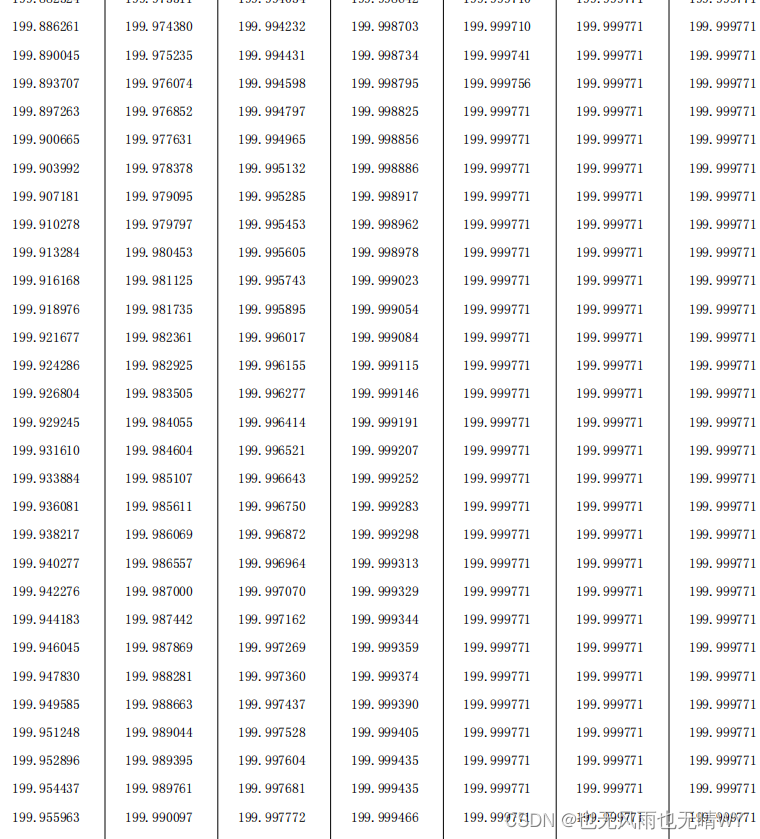
在这里插入图片描述

六抗积分饱和的 PID 控制算法 C 语言实现

所谓的积分饱和现象是指如果系统存在一个方向的偏差，PID 控制器的输出
由于积分作用的不断累加而加大，从而导致执行机构达到极限位置，若控制器输
出 U(k)继续增大，执行器开度不可能再增大，此时计算机输出控制量超出了正
常运行范围而进入饱和区。一旦系统出现反向偏差，u(k)逐渐从饱和区退出。进
入饱和区越深则退出饱和区时间越长。在这段时间里，执行机构仍然停留在极限
位置而不随偏差反向而立即做出相应的改变，这时系统就像失控一样，造成控制
性能恶化，这种现象称为积分饱和现象或积分失控现象。

防止积分饱和的方法之一就是抗积分饱和法，该方法的思路是在计算 u(k)
时，首先判断上一时刻的控制量 u(k-1)是否已经超出了极限范围：如果
u(k-1)>umax，则只累加负偏差; 如果 u(k-1)<umin，则只累加正偏差。从而避
免控制量长时间停留在饱和区。直接贴出代码，不懂的看看前面几节的介绍。

struct _pid{
float SetSpeed; //定义设定值
float ActualSpeed; //定义实际值
float err; //定义偏差值
float err_last; //定义上一个偏差值
float Kp,Ki,Kd; //定义比例、积分、微分系数
float voltage; //定义电压值（控制执行器的变量）
float integral; //定义积分值
float umax;
float umin;
}pid;
void PID_init(){
printf("PID_init begin \n");
pid.SetSpeed=0.0;
pid.ActualSpeed=0.0;
pid.err=0.0;
pid.err_last=0.0;
pid.voltage=0.0;
pid.integral=0.0;
pid.Kp=0.2;
pid.Ki=0.1; //注意，和上几次相比，这里加大了积分环节的值
pid.Kd=0.2;
pid.umax=400;
pid.umin=-200;
printf("PID_init end \n");
}
float PID_realize(float speed){
int index;
PID 控制----C 语言讲解
pid.SetSpeed=speed;
pid.err=pid.SetSpeed-pid.ActualSpeed;
if(pid.ActualSpeed>pid.umax) //灰色底色表示抗积分饱和的实现
{
if(abs(pid.err)>200) //蓝色标注为积分分离过程
{
index=0;
}else{
index=1;
if(pid.err<0)
{
pid.integral+=pid.err;
} }
}else if(pid.ActualSpeed<pid.umin){
if(abs(pid.err)>200) //积分分离过程
{
index=0;
}else{
index=1;
if(pid.err>0)
{
pid.integral+=pid.err;
} }
}else{
if(abs(pid.err)>200) //积分分离过程
{
index=0;
}else{
index=1;
pid.integral+=pid.err;
} }
pid.voltage=pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*(pid.
err-pid.err_last);
pid.err_last=pid.err;
pid.ActualSpeed=pid.voltage*1.0;
return pid.ActualSpeed;
}

最终的测试程序运算结果如下，可以明显的看出系统的稳定时间相对前几次来讲
缩短了不少。
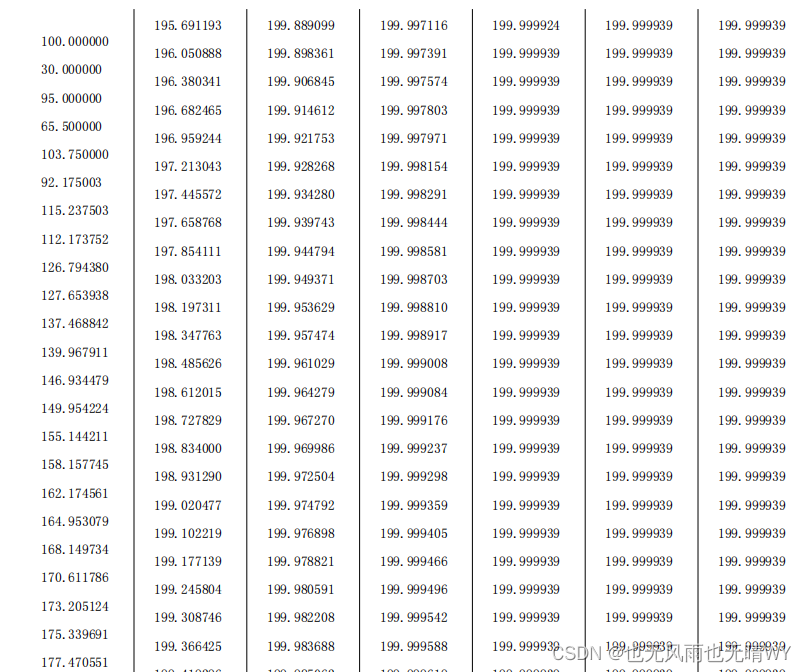
在这里插入图片描述

就讲到这里了，点个赞再走吧！

原文链接：https://blog.csdn.net/cubejava/article/details/125646033

一 PID 算法原理

二 PID 算法的离散化

三 位置型 PID 的 C 语言实现

四 增量型 PID 的 C 语言实现

五 积分分离的 PID 控制算法 C 语言实现

六 抗积分饱和的 PID 控制算法 C 语言实现

你可能也喜欢

三位置型 PID 的 C 语言实现

四增量型 PID 的 C 语言实现

五积分分离的 PID 控制算法 C 语言实现

六抗积分饱和的 PID 控制算法 C 语言实现