神经网络的基本流程
神经网络是一种模仿人脑神经元结构的计算模型,其基本流程主要包括以下几个步骤:
1.数据输入:神经网络通过输入层接收输入数据。这些数据通常是特征向量或者矩阵,表示要处理的问题的各个属性。
2.数据加权与偏置:输入数据在经过神经网络的每个神经元时,都会与一定的权重(W)相乘,然后加上一个偏置值(b)。权重和偏置都是网络在训练过程中需要学习和调整的参数。
3.激活函数:加权求和后的结果会传递给激活函数。激活函数的作用是将神经元的输出结果进行非线性映射,使得神经网络具有更强大的表达能力。常用的激活函数有 ReLU(线性整流函数)、sigmoid、tanh(双曲正切函数)等。
4.隐藏层:隐藏层是神经网络中位于输入层和输出层之间的一层或多层神经元。隐藏层的神经元数量和层数取决于具体问题和网络结构。隐藏层可以提高神经网络的表达能力,捕捉更复杂的数据特征。
5.输出层:输出层是神经网络的最后一层,负责生成网络的预测结果。输出层的神经元数量和激活函数通常取决于具体任务的需求,例如分类问题通常使用 softmax 函数作为激活函数。
6.损失函数:损失函数用于评估神经网络预测结果与实际目标之间的差距。常用的损失函数有均方误差(MSE)、交叉熵损失(Cross-Entropy Loss)等。
7.反向传播与参数更新:通过计算损失函数的梯度,采用梯度下降法或其他优化算法(如 Adam、RMSprop 等)更新神经网络的权重和偏置参数,从而使损失函数最小化。
神经网络的基本流程包含了激活函数这一关键环节,激活函数的选取和设计对于网络的性能具有重要影响。
下面是简单的EWC算法的代码,使用MNIST 数据集和USPS 数据集
import torch
import ssl
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
from torch.utils.data import DataLoader, random_split
# 禁用SSL验证
ssl._create_default_https_context = ssl._create_unverified_context
# Data preparation
transform = transforms.Compose([
transforms.Resize((28,28)),
transforms.ToTensor(),
#.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)) # 对所有通道进行归一化,使其分布在[-1, 1]范围内
])
# train_dataset = datasets.MNIST('./data', train=True, download=True, transform=transform)
#
# #task1_data = [data for data in train_dataset if data[1] < 5]
# #task2_data = [data for data in train_dataset if data[1] >= 5]
# # Split data into two groups
# train_dataset_size = len(train_dataset)
# train_split_sizes = [train_dataset_size // 2, train_dataset_size - train_dataset_size // 2]
# task1_data, task2_data = random_split(train_dataset, train_split_sizes)
#
#
#
# task1_loader = DataLoader(task1_data, batch_size=64, shuffle=True)
# task2_loader = DataLoader(task2_data, batch_size=64, shuffle=True)
#
# test_dataset = datasets.MNIST('./data', train=False, download=True, transform=transform)
#
# #task1_test_data = [data for data in test_dataset if data[1] < 5]
# #task2_test_data = [data for data in test_dataset if data[1] >= 5]
# test_dataset_size = len(test_dataset)
# test_split_sizes = [test_dataset_size // 2, test_dataset_size - test_dataset_size // 2]
# task1_test_data, task2_test_data = random_split(test_dataset, test_split_sizes)
#
# task1_test_loader = DataLoader(task1_test_data, batch_size=64, shuffle=False)
# task2_test_loader = DataLoader(task2_test_data, batch_size=64, shuffle=False)
# 加载 MNIST 数据集
task1_data = datasets.MNIST('./data', train=True, download=True, transform=transform)
task1_test_data = datasets.MNIST('./data', train=False, download=True, transform=transform)
task1_loader = DataLoader(task1_data , batch_size=64, shuffle=True)
task1_test_loader = DataLoader(task1_test_data, batch_size=64, shuffle=False)
# 加载 USPS 数据集
task2_data = datasets.USPS('./data', train=True, download=True, transform=transform)
task2_test_data = datasets.USPS('./data', train=False, download=True, transform=transform)
task2_loader = DataLoader(task2_data, batch_size=64, shuffle=True)
task2_test_loader = DataLoader(task2_test_data, batch_size=64, shuffle=False)
# Model definition
class SimpleNet(nn.Module):
def __init__(self):
super(SimpleNet, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
def forward(self, x):
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2(x), 2))
x = x.view(-1, 320)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
# EWC implementation
class EWC:
def __init__(self, model, dataloader, device, importance=1000):
self.model = model
self.importance = importance
self.device = device
self.params = {n: p.clone().detach() for n, p in self.model.named_parameters() if p.requires_grad}
self.fisher = self._compute_fisher(dataloader)
#计算fisher信息矩阵
def _compute_fisher(self, dataloader):
fisher = {}
for n, p in self.model.named_parameters():
if p.requires_grad:
fisher[n] = torch.zeros_like(p.data)
self.model.train()
for data, target in dataloader:
data, target = data.to(self.device), target.to(self.device)
self.model.zero_grad()
output = F.log_softmax(self.model(data), dim=1)
loss = F.nll_loss(output, target)
loss.backward()
for n, p in self.model.named_parameters():
if p.requires_grad:
fisher[n] += (p.grad ** 2) / len(dataloader)
return fisher
def penalty(self, new_model):
loss = 0
for n, p in new_model.named_parameters():
if p.requires_grad:
_loss = self.fisher[n] * (p - self.params[n]) ** 2
loss += _loss.sum()
return loss * (self.importance / 2)
# Train function
def train(model, dataloader, optimizer, criterion, device, ewc=None, ewc_lambda=0.5):
model.train()
for data, target in dataloader:
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = criterion(output, target)
if ewc is not None:
ewc_loss = ewc.penalty(model)
loss += ewc_lambda * ewc_loss
loss.backward()
optimizer.step()
# Test function
def test(model, dataloader, device):
model.eval()
correct = 0
total = 0
with torch.no_grad():
for data, target in dataloader:
data, target = data.to(device), target.to(device)
output = model(data)
_, predicted = torch.max(output.data, 1)
total += target.size(0)
correct += (predicted == target).sum().item()
accuracy = 100 * correct / total
return accuracy
# Device
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# Initialize model
model = SimpleNet().to(device)
# Train on Task 1
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
criterion = nn.CrossEntropyLoss()
for epoch in range(10):
train(model, task1_loader, optimizer, criterion, device)
task1_accuracy = test(model, task1_test_loader, device)
print(f'Task 1 accuracy: {task1_accuracy}%')
# Save EWC
ewc = EWC(model, task1_loader, device)
# Train on Task 2
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
for epoch in range(10):
train(model, task2_loader, optimizer, criterion, device, ewc=ewc, ewc_lambda=10 )
task2_accuracy = test(model, task2_test_loader, device)
print(f'Task 2 accuracy: {task2_accuracy}%')
# Train on Task 2 but don't have ewc
# optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
#
# for epoch in range(10):
# #训练ewc=none代表不使用ewc算法
# train(model, task2_loader, optimizer, criterion, device, ewc=None)
# task2_accuracy = test(model, task2_test_loader, device)
#
# print(f'Task 2 dont have ewc accuracy: {task2_accuracy}%')
task1_accuracy_new = test(model, task1_test_loader, device)
print(f'Tasknew 1 accuracy: {task1_accuracy_new}%')
task2_accuracy_NEW = test(model, task2_test_loader, device)
print(f'Tasknew 2 accuracy: {task2_accuracy_NEW}%')
知识蒸馏
知识蒸馏就是有两个模型,一个训练好的Teacher模型一个没有训练Student模型,Student模型尽可能的学习到Teacher模型的知识。
软标签
(Soft labels)是指模型输出的类别概率分布,其值通常在0到1之间,而且所有类别的概率之和为1。软标签与硬标签(Hard labels)相对应。
硬标签
是指具有单一类别的确定性标签,通常表示为一个整数或独热编码(One-Hot encoding)向量。
在神经网络中,当网络输出层的激活函数(如softmax)计算出每个类别的概率时,就可以得到软标签。与硬标签相比,软标签包含更多的信息,例如每个类别的置信度,这有助于模型更好地了解不同类别之间的关系。
在知识蒸馏中,软标签起着关键作用。教师网络为每个输入样本生成软标签,学生网络则试图学习这些软标签。通过学习软标签,学生网络可以捕捉到教师网络的潜在知识,从而提高其泛化能力。为了生成更有用的软标签,通常使用温度(Temperature)参数对教师网络的输出进行缩放。较高的温度值会使概率分布更平滑,从而使学生网络更容易捕捉到教师网络的知识。
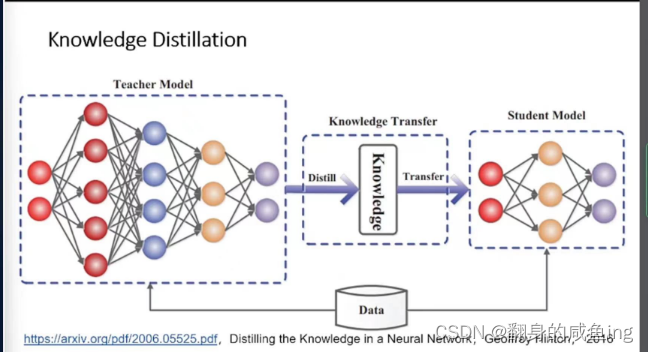
当我们训练神经网络进行分类任务时,网络最终需要输出每个类别的概率值。在这之前,神经网络会将输入数据通过一系列数学运算和非线性变换,最终得到一个未经过 softmax 函数处理的向量。这个向量就是 logits。在 logits 中,每个元素对应一个类别,其值越大表示模型越认为这个样本属于这个类别,但这些值并不一定满足概率分布的要求(比如值域不在 [0,1] 区间内,且值的总和不一定为1)。因此,我们需要经过 softmax 函数的处理,将 logits 转换为一个概率分布,才能最终得到每个类别的概率值。简单来说,logits 就是神经网络分类任务中未经过处理的输出结果,通过 softmax 函数的处理后,我们才能得到具有概率意义的输出。

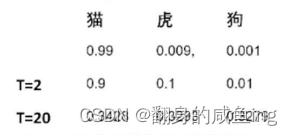
当我像更多的保留软标签也就是不同类别的概率值时可以通过T温度来改变。
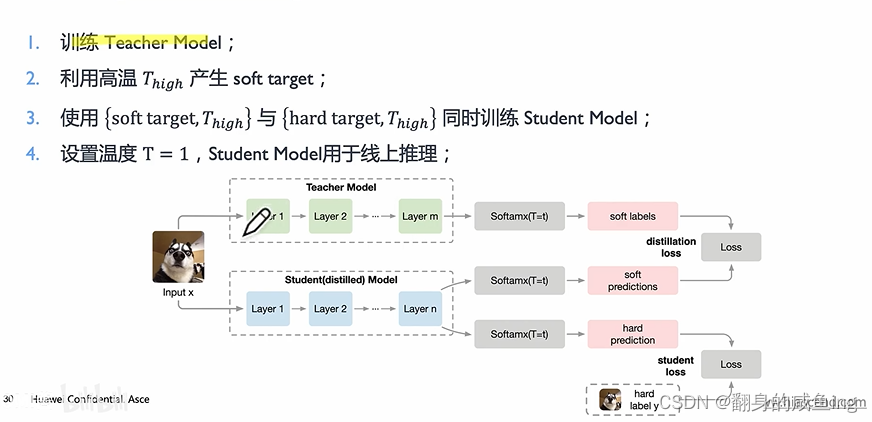
对于怎么训练学生模型,首先训练Teacher模型得到软标签

EWC算法的改进
在EWC(弹性权重共享)中,为了简化计算和降低计算成本,通常会假设费舍尔信息矩阵(Fisher Information Matrix,FIM)是一个对角矩阵。这意味着我们只考虑各个参数对应的费舍尔信息值,而忽略了参数之间的相互作用。
实际上,费舍尔信息矩阵是一个对称矩阵,其非对角元素表示不同参数之间的相关性。然而,在实际应用中,为了降低计算复杂性,通常会采用对角化近似。这种近似虽然可能损失了一些参数之间的相关信息,但在很多情况下,仍能取得较好的性能。
所以,在EWC中使用的费舍尔信息矩阵通常被近似为对角矩阵。这有助于简化计算,并在降低计算成本的同时仍能有效地保护先前任务的知识。
ICaRL
ICaRL算法的整体构造

1)将新得到新类样本和之前存储的旧类样本集共同加到卷积神经网络中训练,来更新当前的模型参数θ
2)因为 K 是事先设定好的,确定增加新类别后,每个类别应该保留的图片数
3)对旧任务 1,…,s-1 每个类别的图片数减少到 m
4)对新任务构建新的样本集 Py,其中 y = [s,…,t],每个类别分别选择 m 张,最后将其加入到总的样本集 P 中
ICaRL中的分类问题

假设我们的iCaRL算法中包含5个类别,每个类别有10个训练样本,每个样本由一个长度为4的特征向量表示。现在有一个测试样本
x
=
[
1
,
2
,
3
,
4
]
x=[1,2,3,4]
x
=
[
1
,
2
,
3
,
4
]
,我们需要使用iCaRL算法对它进行分类。
首先,我们将测试样本输入到ResNet-32神经网络中,得到一个长度为5的输出向量
y
=
[
y
1
,
y
2
,
y
3
,
y
4
,
y
5
]
y=[y_1,y_2,y_3,y_4,y_5]
y
=
[
y
1
,
y
2
,
y
3
,
y
4
,
y
5
]
,其中
y
i
y_i
y
i
表示样本
x
x
x
属于第
i
i
i
个类别的概率值。假设该向量为
y
=
[
0.1
,
0.2
,
0.3
,
0.2
,
0.2
]
y=[0.1,0.2,0.3,0.2,0.2]
y
=
[
0.1
,
0.2
,
0.3
,
0.2
,
0.2
]
,则softmax分类器会将其预测为属于第3个类别。
然而,为了避免遗忘旧类别的知识,我们还需要使用距离最近均值分类器来进行分类。具体而言,我们需要计算测试样本
x
x
x
与每个类别的均值向量之间的欧几里得距离,然后选择距离最近的类别作为该样本的预测类别。假设我们已经计算出每个类别的均值向量如下:
类别1的均值向量:
m
1
=
[
0.9
,
1.0
,
1.1
,
1.2
]
m_1=[0.9,1.0,1.1,1.2]
m
1
=
[
0.9
,
1.0
,
1.1
,
1.2
]
类别2的均值向量:
m
2
=
[
1.2
,
1.3
,
1.4
,
1.5
]
m_2=[1.2,1.3,1.4,1.5]
m
2
=
[
1.2
,
1.3
,
1.4
,
1.5
]
类别3的均值向量:
m
3
=
[
1.4
,
1.5
,
1.6
,
1.7
]
m_3=[1.4,1.5,1.6,1.7]
m
3
=
[
1.4
,
1.5
,
1.6
,
1.7
]
类别4的均值向量:
m
4
=
[
1.1
,
1.2
,
1.3
,
1.4
]
m_4=[1.1,1.2,1.3,1.4]
m
4
=
[
1.1
,
1.2
,
1.3
,
1.4
]
类别5的均值向量:
m
5
=
[
0.8
,
0.9
,
1.0
,
1.1
]
m_5=[0.8,0.9,1.0,1.1]
m
5
=
[
0.8
,
0.9
,
1.0
,
1.1
]
然后,我们计算测试样本
x
x
x
与每个类别的均值向量之间的欧几里得距离,得到距离向量
d
=
[
d
1
,
d
2
,
d
3
,
d
4
,
d
5
]
d=[d_1,d_2,d_3,d_4,d_5]
d
=
[
d
1
,
d
2
,
d
3
,
d
4
,
d
5
]
,其中
d
i
d_i
d
i
表示测试样本
x
x
x
与类别
i
i
i
的均值向量之间的欧几里得距离。具体而言,我们有:
d
1
=
∣
∣
x
−
m
1
∣
∣
=
(
1
−
0.9
)
2
+
(
2
−
1.0
)
2
+
(
3
−
1.1
)
2
+
(
4
−
1.2
)
2
≈
2.24
d_1 = ||x-m_1|| = \sqrt{(1-0.9)^2 + (2-1.0)^2 + (3-1.1)^2 + (4-1.2)^2} \approx 2.24
d
1
=
∣∣
x
−
m
1
∣∣
=
(
1
−
0.9
)
2
+
(
2
−
1.0
)
2
+
(
3
−
1.1
)
2
+
(
4
−
1.2
)
2
≈
2.24
d
2
=
∣
∣
x
−
m
2
∣
∣
=
(
1
−
1.2
)
2
+
(
2
−
1.3
)
2
+
(
3
−
1.4
)
2
+
(
4
−
1.5
)
2
≈
2.24
d_2 = ||x-m_2|| = \sqrt{(1-1.2)^2 + (2-1.3)^2 + (3-1.4)^2 + (4-1.5)^2} \approx 2.24
d
2
=
∣∣
x
−
m
2
∣∣
=
(
1
−
1.2
)
2
+
(
2
−
1.3
)
2
+
(
3
−
1.4
)
2
+
(
4
−
1.5
)
2
≈
2.24
d
3
=
∣
∣
x
−
m
3
∣
∣
=
(
1
−
1.4
)
2
+
(
2
−
1.5
)
2
+
(
3
−
1.6
)
2
+
(
4
−
1.7
)
2
≈
2.24
d_3 = ||x-m_3|| = \sqrt{(1-1.4)^2 + (2-1.5)^2 + (3-1.6)^2 + (4-1.7)^2} \approx 2.24
d
3
=
∣∣
x
−
m
3
∣∣
=
(
1
−
1.4
)
2
+
(
2
−
1.5
)
2
+
(
3
−
1.6
)
2
+
(
4
−
1.7
)
2
≈
2.24
d
4
=
∣
∣
x
−
m
4
∣
∣
=
(
1
−
1.1
)
2
+
(
2
−
1.2
)
2
+
(
3
−
1.3
)
2
+
(
4
−
1.4
)
2
≈
1.41
d_4 = ||x-m_4|| = \sqrt{(1-1.1)^2 + (2-1.2)^2 + (3-1.3)^2 + (4-1.4)^2} \approx 1.41
d
4
=
∣∣
x
−
m
4
∣∣
=
(
1
−
1.1
)
2
+
(
2
−
1.2
)
2
+
(
3
−
1.3
)
2
+
(
4
−
1.4
)
2
≈
1.41
d
5
=
∣
∣
x
−
m
5
∣
∣
=
(
1
−
0.8
)
2
+
(
2
−
0.9
)
2
+
(
3
−
1.0
)
2
+
(
4
−
1.1
)
2
≈
2.24
d_5 = ||x-m_5|| = \sqrt{(1-0.8)^2 + (2-0.9)^2 + (3-1.0)^2 + (4-1.1)^2} \approx 2.24
d
5
=
∣∣
x
−
m
5
∣∣
=
(
1
−
0.8
)
2
+
(
2
−
0.9
)
2
+
(
3
−
1.0
)
2
+
(
4
−
1.1
)
2
≈
2.24
因此,距离测试样本
x
x
x
最近的均值向量是类别4的均值向量
m
4
m_4
m
4
,对应的距离是
d
4
≈
1.41
d_4 \approx 1.41
d
4
≈
1.41
。所以,根据距离最近均值分类器的规则,测试样本
x
x
x
应该被分类为第4个类别。
为新类构建范例集

首先,如果有新的数据集(有旧类和新类),那么将新的数据集和旧的数据集按类融合在一起,求每一个类的平均特征向量(所有特征向量相加除以个数),之后选出M个距离平均特征向量最近的样本作为该类构建范例集,这个步骤包括了对为新类构建范例集的构造也包括了对旧类的更新。
更新特征函数

后面损失函数加了个知识蒸馏,和LWF算法的区别是LWF算法用新数据在旧模型上的表现模拟新数据,而ICarL则是真的保留了新数据