“
使用K-Mean均值算法进行聚类只是一种判断干扰因素的手段,不是最终目的
”
近期有几个特别热衷于调参的小伙伴问我,“那些大神/老师总说通过阶跃响应曲线来调PID参数并不正确,是这样吗”。
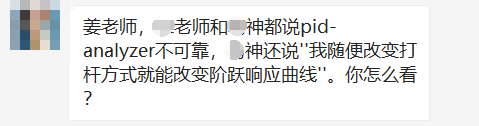
我难以揣测这背后到底有着多少对于数学的恶意,也无法猜测这其中掺杂了多少不懂装懂的尴尬。 但是既然大家对这些工具的恶意这么大,索性今天也就不计字数,给大家粗略解释一下PID-Analyzer和PIDtoolbox的阶跃响应形状不同的原因,以及其背后的反卷积原理。
01
—
为什么同一个LOG会出现截然不同的结果?
简单来说,这是因为
PID-Analyzer直接输出全部阶跃响应帧的平均结果
,而
PIDtoolbox启用了根据稳定时长筛选阶跃响应帧的算法来控制分析数据的质量
。
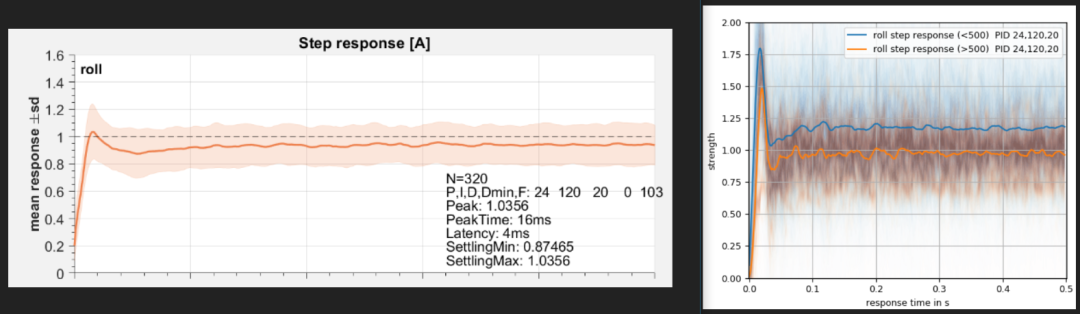
在PIDtoolbox内看起来还算正常的log,在PID-analyzer里则完全超调
查阅代码可知,PID-analyzer在进行维纳反卷积之后直接对全部阶跃响应帧进行了求平均,并进行了图像绘制。
def wiener_deconvolution(self, input, output, cutfreq): # input/output are two-dimensional 输入输出信号均为二维信号 pad = 1024 - (len(input[0]) % 1024) # padding to power of 2, increases transform speed 将 padding设置为2的幂次数以提高变换速度 input = np.pad(input, [[0,0],[0,pad]], mode='constant') # 指定输入信号及模式,下为输出信号 output = np.pad(output, [[0, 0], [0, pad]], mode='constant') H = np.fft.fft(input, axis=-1) G = np.fft.fft(output,axis=-1) freq = np.abs(np.fft.fftfreq(len(input[0]), self.dt)) sn = self.to_mask(np.clip(np.abs(freq), cutfreq-1e-9, cutfreq)) len_lpf=np.sum(np.ones_like(sn)-sn) sn=self.to_mask(gaussian_filter1d(sn,len_lpf/6.)) sn= 10.*(-sn+1.+1e-9) # +1e-9 to prohibit 0/0 situations Hcon = np.conj(H) deconvolved_sm = np.real(np.fft.ifft(G * Hcon / (H * Hcon + 1./sn),axis=-1)) # 此为反卷积核心公式 return deconvolved_sm # 将阶跃响应结果返回输出def stack_response(self, stacks, window): # 绘制阶跃响应曲线 inp = stacks['input&