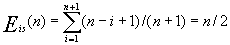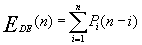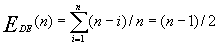顺序表
1. 顺序表的定义
(1) 顺序存储方法
即把线性表的结点按逻辑次序依次存放在一组地址连续的存储单元里的方法。
(2) 顺序表(Sequential List)
用顺序存储方法存储的线性表简称为顺序表(Sequential List)。
2. 结点ai 的存储地址
不失一般性,设线性表中所有结点的类型相同,则每个结点所占用存储空间大小亦相同。假设表中每个结点占用c个存储单元,其中第一个单元的存储地址则是该结点的存储地址,并设表中开始结点a1的存储地址(简称为基地址)是LOC(a1),那么结点ai的存储地址LOC(ai)可通过下式计算(LOC表示获得存储位置的函数):
LOC(ai)= LOC(a1)+(i-1)*c 1≤i≤n
注意:
在顺序表中,每个结点ai的存储地址是该结点在表中的位置i的线性函数。只要知道基地址和每个结点的大小,就可在相同时间内求出任一结点的存储地址。是一种随机存取结构。
通过这个公式,我们可以随时计算出线性表中任意位置的地址,不管它是第一个还是最后一个,都是相同的时间。
那么它的存储时间性能当然就为O(1),我们通常称为随机存储结构。
3.顺序表类型定义
#define ListSize 100 //表空间的大小可根据实际需要而定,这里假设为100
typedef int DataType; //DataType的类型可根据实际情况而定,这里假设为int
typedef struct {
DataType data[ListSize];//向量data用于存放表结点
int length;//当前的表长度
}SeqList;
注意:
① 用向量这种顺序存储的数组类型存储线性表的元素外,顺序表还应该用一个变量来表示线性表的长度属性,因此用结构类型来定义顺序表类型。
② 存放线性表结点的向量空间的大小ListSize应仔细选值,使其既能满足表结点的数目动态增加的需求,又不致于预先定义过大而浪费存储空间。
③ 由于C语言中向量的下标从0开始,所以若L是SeqList类型的顺序表,则线性表的开始结点a1和终端结点an分别存储在L.data[0]和L.Data[L.length-1]中。
④ 若L是SeqList类型的指针变量,则a1和an分别存储在L->data[0]和L->data[L->length-1]中。
4.顺序表的特点
顺序表是用向量实现的线性表,向量的下标可以看作结点的相对地址。因此顺序表的的特点是逻辑上相邻的结点其物理位置亦相邻。
顺序表上实现的基本运算
1.表的初始化
void InitList(SeqList *L)
{\\顺序表的初始化即将表的长度置为0
L->length=0;
}
2.求表长
int ListLength(SeqList *L)
{ \\求表长只需返回L->length
return L->length;
}
3.取表中第i个结点
DataType GetNode(L,i)
{\\取表中第i个结点只需返回和L->data[i-1]即可
if (i<1||i> L->length-1)
Error("position error");
return L->data[i-1];
}
4.查找值为x的结点
【参见参考书】
5. 插入
(1) 插入运算的逻辑描述
线性表的插入运算是指在表的第i(1≤i≤n+1)个位置上,插入一个新结点x,使长度为n的线性表:
(a1,…,ai-1,ai,…an)
变成长度为n+1的线性表:
(a1,…,ai-1,x,ai,…an)
注意:
① 由于向量空间大小在声明时确定,当L->length≥ListSize时,表空间已满,不可再做插入操作
② 当插入位置i的值为i>n或i<1时为非法位置,不可做正常插入操作
(2) 顺序表插入操作过程
在顺序表中,结点的物理顺序必须和结点的逻辑顺序保持一致,因此必须将表中位置为n ,n-1,…,i上的结点,依次后移到位置n+1,n,…,i+1上,空出第i个位置,然后在该位置上插入新结点x。仅当插入位置i=n+1时,才无须移动结点,直接将x插入表的末尾。
具体过程见【动画演示】
(3)具体算法描述
void InsertList(SeqList *L,DataType x,int i)
{//将新结点 x插入L所指的顺序表的第i个结点ai的位置上
int j;
if (i<1||i>L->length+1)
Error("position error");//非法位置,退出运行
if (L->length>=ListSize)
Error("overflow"); //表空间溢出,退出运行
for(j=L->length-1;j>=i-1;j--)
L->data[j+1]=L->data[j];//结点后移
L->data[i-1]=x; //插入x
L->Length++; //表长加1
}
(4)算法分析
① 问题的规模
表的长度L->length(设值为n)是问题的规模。
② 移动结点的次数由表长n和插入位置i决定
算法的时间主要花费在for循环中的结点后移语句上。该语句的执行次数是n-i+1。
当i=n+1:移动结点次数为0,即算法在最好时间复杂度是0(1)
当i=1:移动结点次数为n,即算法在最坏情况下时间复杂度是0(n)
③ 移动结点的平均次数Eis(n)
其中:
在表中第i个位置插入一个结点的移动次数为n-i+1
pi表示在表中第i个位置上插入一个结点的概率。不失一般性,假设在表中任何合法位置(1≤i≤n+1)上的插入结点的机会是均等的,则
p1=p2=…=pn+1=1/(n+1)
因此,在等概率插入的情况下,
即在顺序表上进行插入运算,平均要移动一半结点。
6. 删除
(1)删除运算的逻辑描述
线性表的删除运算是指将表的第i(1≤i≤n)个结点删去,使长度为n的线性表
(a1,…,ai-1,ai,ai+1,…,an)
变成长度为n-1的线性表
(a1,…,ai-1,ai+1,…,an)
注意:
当要删除元素的位置i不在表长范围(即i<1或i>L->length)时,为非法位置,不能做正常的删除操作
(2)顺序表删除操作过程
在顺序表上实现删除运算必须移动结点,才能反映出结点间的逻辑关系的变化。若i=n,则只要简单地删除终端结点,无须移动结点;若1≤i≤n-1,则必须将表中位置i+1,i+2,…,n的结点,依次前移到位置i,i+1,…,n-1上,以填补删除操作造成的空缺。其删除过程【参见动画演示】
(3)具体算法描述
void DeleteList(SeqList *L,int i)
{//从L所指的顺序表中删除第i个结点ai
int j;
if(i<1||i>L->length)
Error("position error"); //非法位置
for(j=i;j<=L->length-1;j++)
L->data[j-1]=L->data[j]; //结点前移
L->length--; //表长减小
}
(4)算法分析
①结点的移动次数由表长n和位置i决定:
i=n时,结点的移动次数为0,即为0(1)
i=1时,结点的移动次数为n-1,算法时间复杂度分别是0(n)
②移动结点的平均次数EDE(n)
其中:
删除表中第i个位置结点的移动次数为n-i
pi表示删除表中第i个位置上结点的概率。不失一般性,假设在表中任何合法位置(1≤i≤n)上的删除结点的机会是均等的,则
p1=p2=…=pn=1/n
因此,在等概率插入的情况下,
顺序表上做删除运算,平均要移动表中约一半的结点,平均时间复杂度也是0(n)。
转载自:
http://student.zjzk.cn/course_ware/data_structure/web/xianxingbiao/xianxingbiao2.2.1.htm
参考:
http://blog.csdn.net/hguisu/article/details/7673703
(完成的例子参考,c语言实现)
http://blog.csdn.net/lincyang/article/details/8606682
(例子实现)
http://hjj20040849.iteye.com/blog/1816838(例子实现)
总结:
http://blog.fishc.com/1718.html
顺序存储结构封装需要三个属性:
存储空间的起始位置: 数组data,它的存储位置就是线性表存储空间的存储位置。
线性表的最大存储容量:数组的长度MaxSize。
线性表的当前长度:length。
注意,数组的长度与线性表的当前长度需要区分一下:
数组的长度是存放线性表的存储空间的总长度,一般初始化后不变。
而线性表的当前长度是线性表中元素的个数,是会变化的。
现在我们分析一下,插入和删除的时间复杂度。
最好的情况:插入和删除操作刚好要求在最后一个位置操作,因为不需要移动任何元素,所以此时的时间复杂度为O(1)。
最坏的情况:如果要插入和删除的位置是第一个元素,那就意味着要移动所有的元素向后或者向前,所以这个时间复杂度为O(n)。
至于平均情况,就取中间值O((n-1)/2)。
按照前边游戏秘籍指导,平均情况复杂度简化后还是O(n)。
线性表顺序存储结构的优缺点
线性表的顺序存储结构,在存、读数据时,不管是哪个位置,时间复杂度都是O(1)。而在插入或删除时,时间复杂度都是O(n)。
这就说明,它比较适合元素个数比较稳定,不经常插入和删除元素,而更多的操作是存取数据的应用。
那我们接下来给大家简单总结下线性表的顺序存储结构的优缺点:
优点:
无须为表示表中元素之间的逻辑关系而增加额外的存储空间。
可以快速地存取表中任意位置的元素。
缺点:
插入和删除操作需要移动大量元素。
当线性表长度变化较大时,难以确定存储空间的容量。
容易造成存储空间的“碎片”。
为什么当插入和删除时,就要移动大量的元素?
原因就在于相邻两元素的存储位置也具有邻居关系,它们在内存中的位置是紧挨着的,中间没有间隙,当然就无法快速插入和删除。