博客

1、TSP问题

1.1 TSP问题定义

旅行商问题（Traveling Salesman Problem，TSP）称之为货担郎问题，TSP问题是一个经典组合优化的NP完全问题，组合优化问题是对存在组合排序或者搭配优化问题的一个概括，也是现实诸多领域相似问题的简化形式。

1.2 TSP问题解法

传统精确算法：穷举法，动态规划

近似处理算法：贪心算法，改良圈算法，双生成树算法

智能算法：模拟退火，粒子群算法，蚁群算法，遗传算法等

2、遗传算法

2.1 遗传算法简介

遗传算法的实质是通过群体搜索技术，根据适者生存的原则逐代进化，最终得到最优解或准最优解。它必须做以下操作：初始群体的产生、求每一个体的适应度、根据适者生存的原则选择优良个体、被选出的优良个体两两配对，通过随机交叉其染色体的基因并随机变异某些染色体的基因生成下一代群体，按此方法使群体逐代进化，直到满足进化终止条件。

2.2 实现方法

1. 根据具体问题确定可行解域，确定一种编码方法，能用数值串或字符串表示可行解域的每一解。
2. 对每一解应有一个度量好坏的依据，它用一函数表示，叫做适应度函数，一般由目标函数构成。
3. 确定进化参数群体规模、交叉概率、变异概率、进化终止条件。

3、实例分析

3.1 案例导入

我方有一个基地，经度和纬度为（70，40）。假设我方飞机的速度为1000km/h。我方派一架飞机从基地出发，侦察完所有目标，再返回原来的基地。在每一目标点的侦察时间不计，求该架飞机所花费的时间（假设我方飞机巡航时间可以充分长）。已知100个目标的经度、纬度如下表所列。







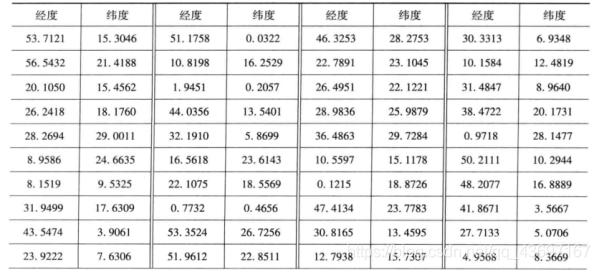
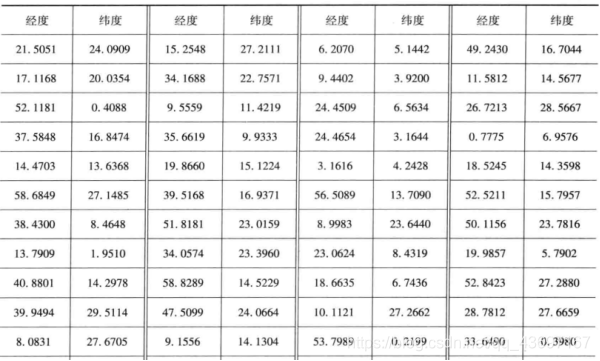
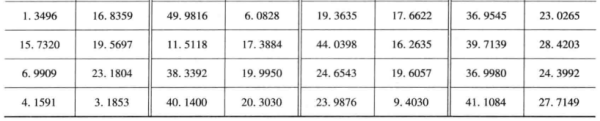
解：

3.2 模型及算法

求解的遗传算法的参数设定如下：

种群大小M=50；最大代数G=100;

交叉率pc=1，交叉概率为1能保证种群的充分进化；

变异概率pm=0.1，一般而言，变异发生的可能性较小。

1. 编码策略
   

2. 初始种群
   
   

3. 目标函数
   
   

4. 交叉操作
   
   

5. 变异操作
   

6. 选择
   
   

3.3 算法流程图

4、效果及代码展示

4.1 结果：

最短距离：3.9365e+04 km 最短时间：39.4h

巡航路径：

4.2代码（MATLAB语言）

clc,clear
sj0=load('sj.txt');       %加载100个目标的数据
x=sj0(:,1:2:8);
x=x(:);
y=sj0(:,2:2:8); 
y=y(:);
sj=[x y]; 
d1=[70,40]; 
sj=[d1;sj;d1