Modeling Relational Data with Graph Convolutional Networks论文学习笔记2

5.实验评估
- 5.1 实体分类实验
- 5.2 链路预测实验
6. 展望

内容过长，论文的前半部分内容请查看

Modeling Relational Data with Graph Convolutional Networks论文学习笔记1

5.实验评估

5.1 实体分类实验

未了推测（e.g.实体类别），一个成功的模型需要能解释这个实体与其他相关实体的关系。

数据集

Resource Description Framework (RDF) format (Ristoski, de Vries, and Paulheim 2016): AIFB, MUTAG, BGS, and AM. 数据集中的关系不必一定编码为有向的subject-object关系，也可以编码为实体的某一特点存在与否。

目的

：节点的特性分类。各数据集统计描述如下表：

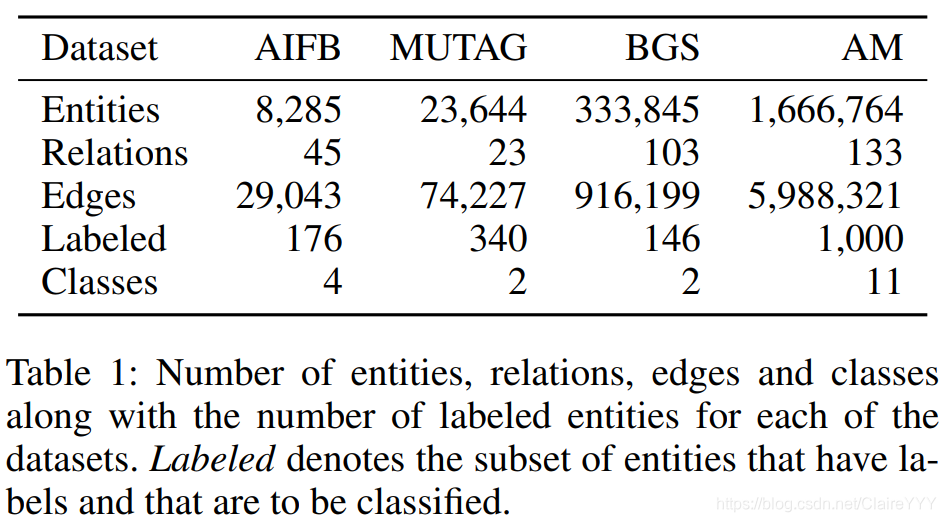
在这里插入图片描述

文章移除了用来产生节点标签的关系：

employs

and

affiliation

for AIFB,

isMutagenic

for MUTAG,

hasLithogenesis

for BGS, and

objectCategory

and

material

for AM。

Baselines基线

作为实验的基准，以最近的艺术级的分类结果进行比较：

RDF2Vec

embeddings (Ristoski and Paulheim 2016), Weisfeiler-Lehman kernels (

WL

) (Shervashidze et al. 2011; de Vries and de Rooij 2015), and hand-designed feature extractors (

Feat

) Paulheim and Fumkranz 2012)。Feat集合了从每个有标签节点的入度和出度获取特征向量。RDF2Vec提取了有标签图的游走然后使用Skipgram模型产生实体嵌入（用做随后的分类）。所有的实体分类实验在CPU和64GB存储运行。

结果

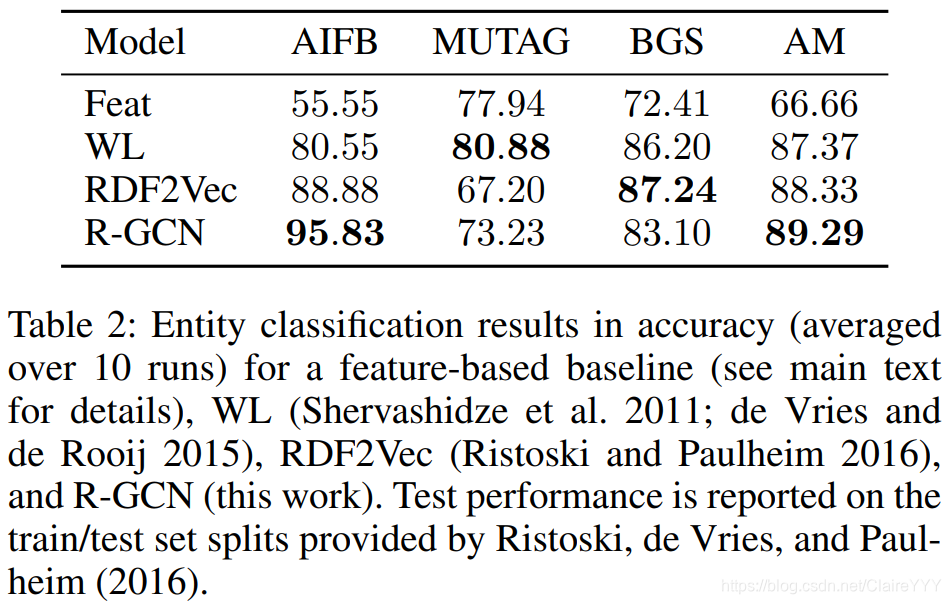
在这里插入图片描述

本实验进一步拨出了20％的训练集作为超参数调整的验证集。对于R-GCN，表格展示的是16个hidden units（10 for AM）的2层模型，基函数分解（公式2），以及使用学习率0.01的Adam训练50个epochs。归一化常数c

_{i,r}

$_{i, r}$

=

∣

\lvert {N_i^r} \rvert

$∣ N_{i}^{r} ∣$

。

在AIFB与AM数据集上我们的方法表现良好，但另外两个数据集较差，原因可能是使用了固定的归一化常数，后期可采用注意力机制（数据依赖的注意力权重

a_{ij,r}

$a_{i j, r}$

，

∑_{j,r}a_{ij,r}=1

$\sum_{j, r} a_{i j, r} = 1$

）进行改进。

5.2 链路预测实验

R-GCN是关系型数据的有效编码器，结合评分函数（即图3b中的解码器）为知识库中的三元组进行链路预测。

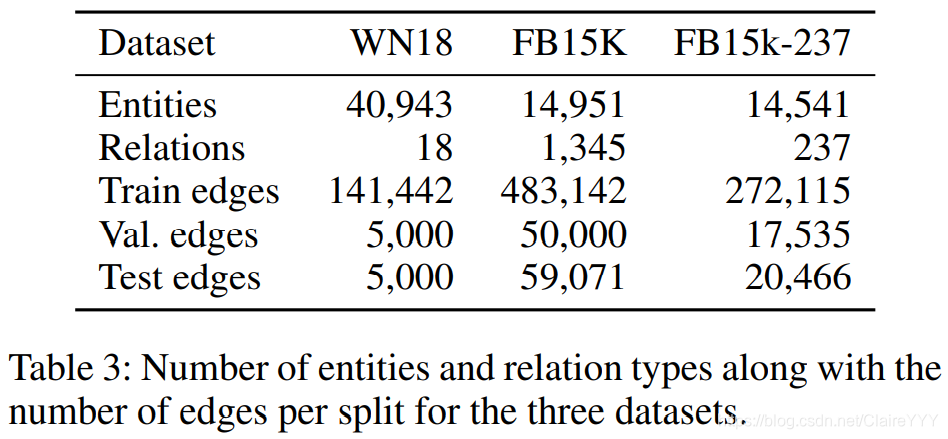
数据集

链路预测算法在FB15k（关系型数据库Freebase的亚集）、WN18（包含单词间词汇关系的WordNet的亚集）数据集上进行评估。原数据集存在相反三元组对

(

)

t=(e_1,r,e_2)

$t = (e_{1}, r, e_{2})$

和

′

(

−

)

t’=(e_2,r^{-1},e_1)

$t^{'} = (e_{2}, r^{- 1}, e_{1})$

，

t

$t$

在训练集，

′

t’

$t^{'}$

在测试集。这会减少一大部分受影响三元组对记忆的预测任务。所以本文选择移除了这些三元组对的FB15k-237数据集。

在这里插入图片描述

Baselines基线

这两个实验的共同基准是

直接优化DistMult

，这个因数分解策略在标准数据集上表现良好，此外，对应于我们模型的版本，该版本具有固定实体嵌入，代替了第4节中所述的R-GCN编码器。作为第二个基准，我们增加了简单的基于邻域的

LinkFeat算法

（ proposed in Toutanova and Chen (2015)）。

我们进一步比较了FB15k和WN18的两个最新链路预测模型ComplEx（Trouillon等人2016）和HolE（Nickel，Rosasco和Poggio 2015）。ComplEx通过将DistMult泛化为复杂域来进行非对称关系的建模，而HolE用循环相关替换向量矩阵乘积。最后，包括与两种经典算法-CP（Hitchcock 1927）和TransE（Bordes等人2013）的比较。

结果

两个常用的评估度量：

MRR: mean reciprocal rank
Hits@n

两种评估度量都可以在原始设置和过滤设置中计算。本文同时报告了原始和过滤MRR(过滤MRR被认为更可靠),及过滤Hits at 1，3，10。

我们评估各个验证拆分上的超参数选择并发现定义为c

_{i,r}

$_{i, r}$

=c

_i

$_{i}$

=

∑_{r}

$\sum_{r}$

∣

\lvert {N_i^r} \rvert

$∣ N_{i}^{r} ∣$

的归一化常数效果最好。

对于FB15k和WN18

：运用基函数分解（公式2）with两个基函数，和一个200维嵌入的编码层。

对于FB15k-237

：块分解（公式3）表现最好，使用2层5×5的块维度和500维的嵌入。归一化之前通过边丢失进行规则化，self-loop的丢失率为0.2，其他边的丢失率为0.4。Apply

l

$l$

2 regularization to the decoder with a penalty of 0.01。

使用学习率为0.01的Ddam优化程序（Kingma and Ba 2014）。对于基线和其他因式分解，我们从Trouillon等人的论文中找到了最佳的参数（2016）——除了FB15k-237的维度，为使系统具有可比性，我们保持相同数量的负样本（

w

$w$

=1）。不论是基线还是我们的模型，我们都使用了full-batch优化。

FB15k数据集中，与R-GCN模型的设计相比，以相反关系形式的局部上下文将主导因式分解的性能。如图4，在我们的模型在具有高度（high degree）的节点（subject和object实体的平均度–度矩阵中的值？？）处表现得更好。同时观察到两个模型具有互补性，说明将两模型的优势结合在一个模型（R-GCN+）中将更好。
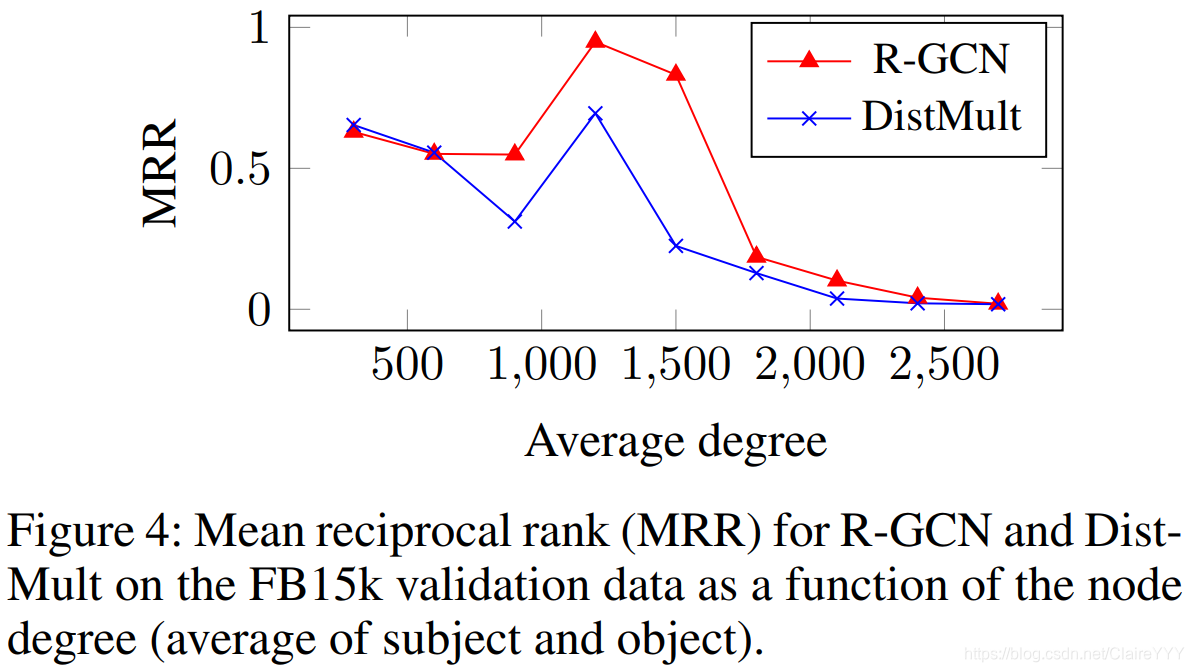
在这里插入图片描述

我们期望，R-GCN+在局部和远距离信息都能提供强烈solutions的数据库（FB15k和WN18）中将比单独的两个模型表现得好，但是在局部关系并不突出的数据集（FB15-237）中不会出现这种优势。为了验证以上期望，在FB15k数据集上评估了结合后的模型（R-GCN+）：

(

)

−

(

)

−

(

−

)

(

)

f(s,r,t)_{R-GCN+}=αf(s,r,t)_{R-GCN}+(1-α)f(s,r,t)_{DistMult}

$f (s, r, t)_{R - G C N +} = α f (s, r, t)_{R - G C N} + (1 - α) f (s, r, t)_{D i s t M u l t}$

，

α

$α$

=0.4。

如图4：R-GCN和R-GCN+比基线DistMult表现好，但是LinkFeat算法又比其他的方法表现得好——*相反关系三元组对高度表达数据的影响。*尽管R-GCN解码器（DistMult）不能清楚地建模非对称关系，但R-GCN+在数据集FB15k中比ComplEx表现好——

表明将R-GCN编码器和 ComplEx评分函数（解码器）结合起来可能是未来的工作方向。

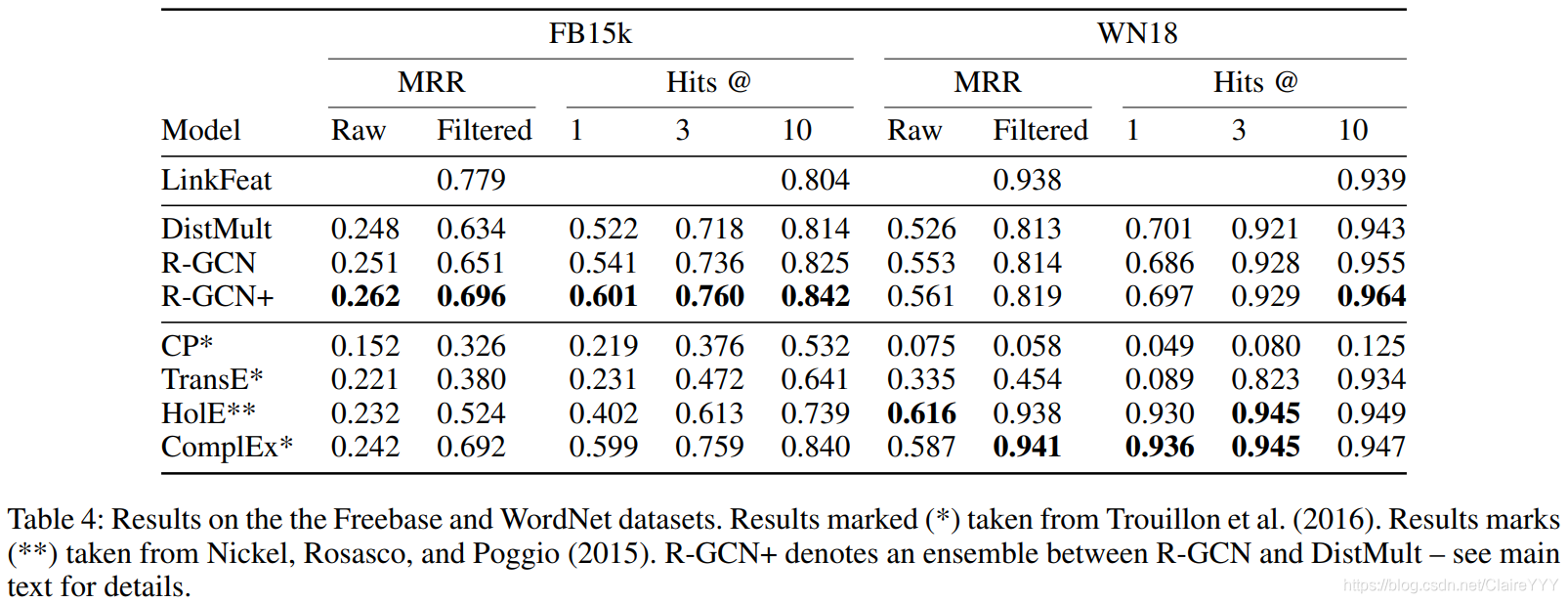
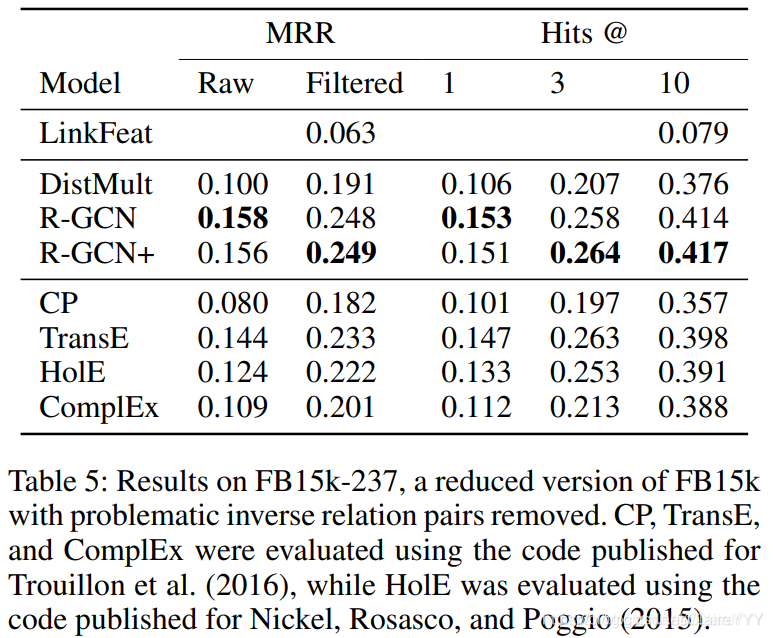
表5是数据集FB15k-237的结果，R-GCN优于DistMult基线——强调了单独编码模型的重要性。正如之前期望，R-GCN与R-GCN+在此数据集上表现相当。尽管依赖于DistMult解码器，但在不使用编码器的情况下，其性能相对较弱，因此R-GCN模型与其他因数分解方法相比更具有优势。

在这里插入图片描述

6. 展望

图片自编码模型可以结合其他因式分解模型，e.g.ComplEx (Trouillon et al. 2016)，更好地适应于非对称关系建模；
为解决本文方法的可扩展性，有必要探索亚采样技术，e.g.Hamilton, Ying, and Leskovec (2017)；
用依赖数据的注意力机制来替换当前在相邻节点和关系类型上求和的形式。
除了建模知识库之外，R-GCN还可推广到其他关系分解模型已被证明是有效的应用中（例如关系提取）。

原文链接：https://blog.csdn.net/ClaireYYY/article/details/111470794

Modeling Relational Data with Graph Convolutional Networks论文学习笔记2

5.实验评估

5.1 实体分类实验

5.2 链路预测实验

6. 展望

你可能也喜欢