决策树<
朴素贝叶斯< K
NN
K近邻算法:根据距离来做排序,距离哪些同类的数据比较近则属于哪一类
(1)从计算结果直观上来看,在这三种算法中,KNN算法的计算准确率普遍较高,且
kNN算法在训练数据与测试数据的比例为9:1时,其准确率达到90%以上。
但是在每次计算测试数据的类别时,都要进行与训练数据的比较。在这种情况下,其复杂度随着数据量的增大而迅速增长。
(2)决策树在递归地产生决策树时,其枝叶较繁杂,且对未知的测试数据的分类却没那么准确,会出现过拟合现象。
在简化决策树为二叉树后,其准确率提高,且二叉树型的决策树在分类时更加简洁。但对于连续性数据,首先应该将数据进行离散化才能使用决策树。
(3)朴素贝叶斯算法在拉普拉斯平滑修正后,
其性能在kNN和决策树之间,但相对于kNN算法,朴素贝叶斯算法的准确率较之低。
朴素贝叶斯算法的优点在于其在数据量较少时仍然适用,且对于多种属性的数据集的效果良好。但其不适用于连续性数据,只能用于离散数据。
一、k-近邻算法原理
简单地说,K-近邻算法采用测量不同特征值之间的距离方法进行分类。
- 优点:精度高、对异常值不敏感、无数据输入假定。
- 缺点:时间复杂度高、空间复杂度高。
- 适用数据范围:数值型和标称型。
工作原理
存在一个样本数据集合,也称作训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一数据与所属分类的对应关系。输人没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似数据(最近邻)的分类标签。
一般来说,我们只选择样本数据集中前K个最相似的数据,这就是K-近邻算法中K的出处,
通常K是不大于20的整数。
最后 ,选择K个最相似数据中出现次数最多的分类,作为新数据的分类。
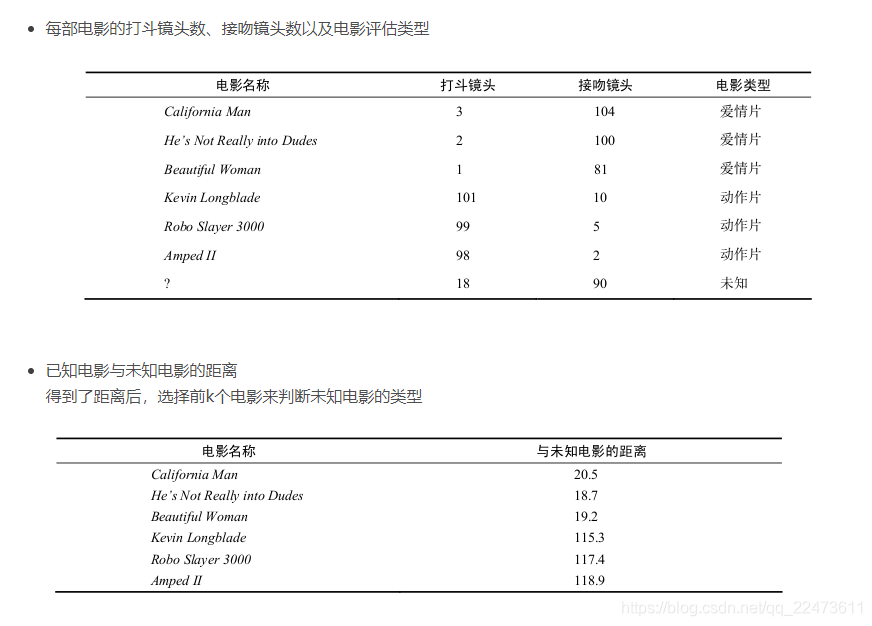

欧几里得距离(Euclidean Distance)
欧氏距离是最常见的距离度量,衡量的是多维空间中各个点之间的绝对距离。公式如下:


k-近邻算法步骤如下:
- 计算已知类别数据集中的点与当前点之间的距离;
- 按照距离递增次序排序;
- 选取与当前点距离最小的k个点;
- 确定前k个点所在类别的出现频率;
- 返回前k个点所出现频率最高的类别作为当前点的预测分类。
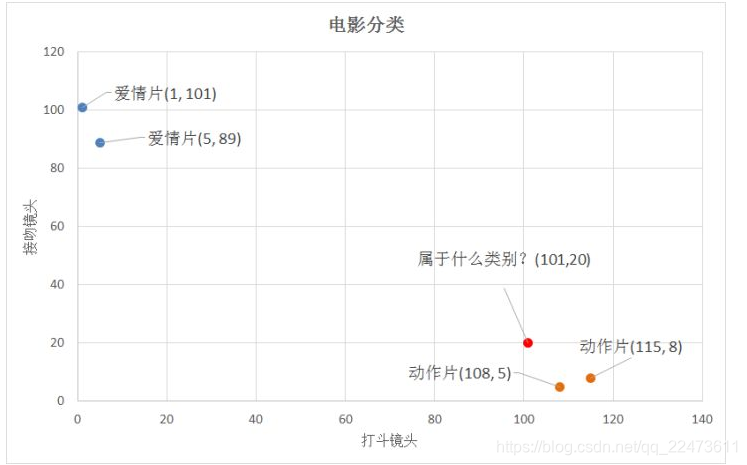
比如,现在我这个k值取3,那么在电影例子中,按距离依次排序的三个点分别是动作片(108,5)、动作片(115,8)、爱情片(5,89)。在这三个点中,动作片出现的频率为三分之二,爱情片出现的频率为三分之一,所以该红色圆点标记的电影为动作片。这个判别过程就是k-近邻算法。
import numpy as np
def createDataSet():
"""创建数据集"""
# 每组数据包含打斗数和接吻数;
group = np.array([[3, 104], [2, 100], [1, 81], [101, 10], [99, 5], [98, 2]])
# 每组数据对应的标签类型;
labels = ['Roman', 'Roman', 'Roman', 'Action', 'Action', 'Action']
return group, labels
def classify(inx, dataSet, labels, k):
"""
KNN分类算法实现
:param inx:要预测电影的数据, e.g.[18, 90]
:param dataSet:传入已知数据集,e.g. group 相当于x
:param labels:传入标签,e.g. labels相当于y
:param k:KNN里面的k,也就是我们要选择几个近邻
:return:电影类新的排序
"""
dataSetSize = dataSet.shape[0] # (6,2) -- 6行2列 ===> 6 获取行数
# tile会重复inx, 把它重复成(dataSetSize, 1)型的矩阵
# (x1 - y1), (x2 - y2)
diffMat = np.tile(inx, (dataSetSize, 1)) - dataSet
# 平方
sqDiffMat = diffMat ** 2
# 相加, axis=1行相加
sqDistance = sqDiffMat.sum(axis=1)
# 开根号
distance = sqDistance ** 0.5
# 排序索引: 输出的是序列号index, 而不是值
sortedDistIndicies = distance.argsort()
# print(sortedDistIndicies)
classCount = {}
for i in range(k):
# 获取排前k个的标签名;
voteLabel = labels[sortedDistIndicies[i]]
classCount[voteLabel] = classCount.get(voteLabel, 0) + 1
sortedClassCount = sorted(classCount.items(),
key=lambda d: float(d[1]),
reverse=True)
return sortedClassCount[0][0]
if __name__ == '__main__':
group, label = createDataSet()
print( group," \n ", label," \n " )
result = classify([18, 90], group, label, 5)
print("\n测试的电影类型:", result)
二、改进约会网站的配对效果
2、项目数据
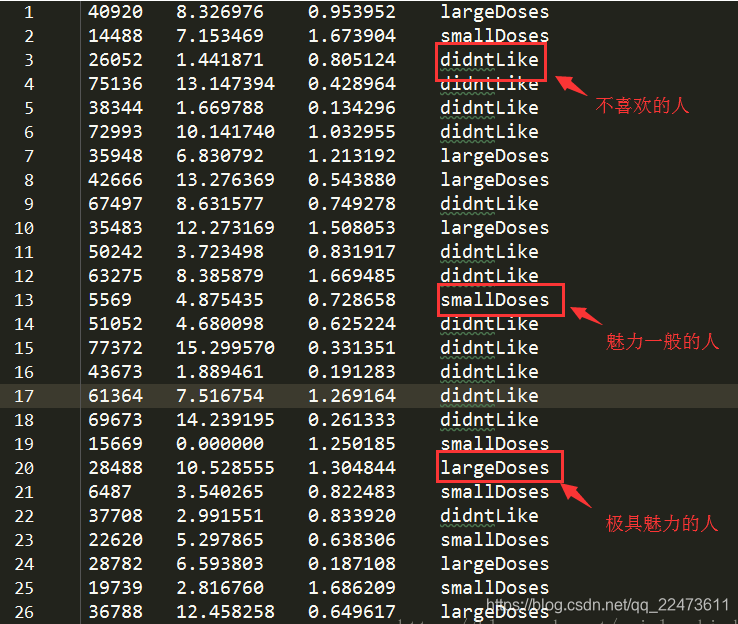
海伦收集约会数据已经有了一段时间,她把这些数据存放在文本文件datingTestSet.txt中,每个样本数据占据一行,总共有1000行。
海伦收集的样本数据主要包含以下3种特征:
1、每年获得的飞行常客里程数
2、玩视频游戏所消耗时间百分比
3、每周消费的冰淇淋公升数
数据格式如下
3、K-近邻算法的一般流程
(1)
收集数据
:提供文本文件。
(2)
准备数据
:使用Python解析文本文件。
(3)
分析数据
:使用Matplotlib画二维扩散图。
(4)
测试算法
:使用文本文件的部分数据作为测试样本,计算错误率。
(5)
使用算法
:错误率在可接受范围内,就可以运行k-近邻算法进行分类。
from numpy import *
import operator
from os import listdir
'''
使用 kNN 进行分类(约会网站配对)
@param inX:用于分类的数据向量
@param dataSet:训练样本集
@param labels:标签向量
@param k:用于选择最近邻的数目
计算当前点,与其余所有点的距离最短则被归为此类
'''
def classify0(inX, dataSet, labels, k):
dataSetSize = dataSet.shape[0]
# 求inX与数据集中各个样本的欧氏距离
diffMat = tile(inX, (dataSetSize, 1)) - dataSet # numpy中的tile函数将inX复制为重复的dataSize个行和重复的1列,功能相当于MATLAB中的repmat
sqDiffMat = diffMat ** 2
sqDistances = sqDiffMat.sum(axis=1) # 按照x轴相加
distances = sqDistances ** 0.5
sortedDistIndicies = distances.argsort() # 从小到大排序后,返回索引
# 字典,key存储第i小的标签值,value为标签的次数
classCount = {}
for i in range(k):
voteIlabel = labels[sortedDistIndicies[i]] # 取第i个小的标签值
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1 # 根据标签统计标签次数,如果没找到返回0。统计前k个候选者中标签出现的次数
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) # operator.itemgetter(1) 按照第2个元素,即标签出现的次数对classCount从大到小排序
# print(sortedClassCount) # 测试结果 [('B', 2), ('A', 1)]
return sortedClassCount[0][0] # 返回最终的类别,即标签值key
'''
读取文本记录,提取特征矩阵和标签向量
@param filename:文件名(如 datingTestSet2.txt)
'''
def file2matrix(filename):
fr = open(filename)
numberOfLines = len(fr.readlines()) # 得到文件行数
returnMat = zeros((numberOfLines, 3)) # 构造一个numberOfLines行3列的全0矩阵,3列代表3个特征,用来存储特征
classLabelVector = [] # 存储标签向量
fr = open(filename)
index = 0
for line in fr.readlines(): # 读文件时,每一行都是一个字符串,故line就是一个字符串
line = line.strip() # 去掉一行字符串line的前后空格
listFromLine = line.split('\t') # 以 '\t' 为切片,切成List,存储各个特征和最后一行的标签值
returnMat[index, :] = listFromLine[0:3] # 存储特征
classLabelVector.append(int(listFromLine[-1])) # 存储标签值
index += 1
return returnMat, classLabelVector
'''
归一化数值
@param dataSet:训练样本集
'''
def autoNorm(dataSet):
minVals = dataSet.min(0) # 0代表从列中取最小值
maxVals = dataSet.max(0)
ranges = maxVals - minVals
normDataSet = zeros(shape(dataSet)) # 构造一个和dataSet一样大小的矩阵
m = dataSet.shape[0]
normDataSet = dataSet - tile(minVals, (m, 1))
normDataSet = normDataSet / tile(ranges, (m, 1)) # 特征值相除,得到正则化后的新值
return normDataSet, ranges, minVals
'''
# 测试归一化数值
datingDataMat, datingLabels = file2matrix('datingTestSet2.txt')
normMat, ranges, minVals = autoNorm(datingDataMat)
print(normMat)
print(ranges)
print(minVals)
'''
def datingClassTest():
hoRatio = 0.08 # 随机挖去 10% 的数据作为测试集
datingDataMat, datingLabels = file2matrix('datingTestSet2.txt') # 加载数据文件
normMat, ranges, minVals = autoNorm(datingDataMat)
m = normMat.shape[0]
numTestVecs = int(m * hoRatio) # 随机挖去的行数
errorCount = 0.0
for i in range(numTestVecs):
# 前numTestVecs条作为测试集(一个一个测试),后面的数据作为训练样本,训练样本的标签,3个近邻
classifierResult = classify0(normMat[i, :], normMat[numTestVecs:m, :], datingLabels[numTestVecs:m], 3)
print("the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]))
if (classifierResult != datingLabels[i]): errorCount += 1.0
print("The number of errr is: %d" % int(errorCount))
print("The total error rate is: %f" % (errorCount / float(numTestVecs)))
# 测试分类错误率,错误分类个数
datingClassTest()
'''
the classifier came back with: 3, the real answer is: 3
………………
the classifier came back with: 3, the real answer is: 3
The number of errr is: 2
The total error rate is: 0.025000
'''