计算机视觉中的位姿估计
1. 问题描述
位姿估计在计算机视觉领域扮演着十分重要的角色。在使用视觉传感器估计机器人位姿进行控制、机器人导航、增强现实以及其它方面都有着极大的应用。位姿估计这一过程的基础是找到现实世界和图像投影之间的对应点。然后根据这些点对的类型,如2D-2D, 2D-3D, 3D-3D,采取相应的位姿估计方法。我们通常称把根据已知点对估计位姿的过程称为求解PnP。
2. 2D-2D:对极几何
假设我们从两幅图像中,得到了一对配对好的特征点。如下图所示,
p
1
p_{1}
p
1
和
p
2
p_{2}
p
2
是两幅图像中匹配的特征点,
O
1
O_{1}
O
1
、
O
2
O_{2}
O
2
是两个相机中心。

如果我们有若干对这样的特征点,我们就可以通过这些二维图像点的对应关系,恢复出两帧之间摄像机的运动。以上图为例,我们希望求取两帧图像
I
1
I_{1}
I
1
和
I
2
I_{2}
I
2
之间相机的运动。设第一帧到第二帧的运动为
R
R
R
,
t
t
t
,
P
P
P
点在第一帧相机坐标系下的坐标为
P
=
[
X
,
Y
,
Z
]
T
P=[X,Y,Z]^T
P
=
[
X
,
Y
,
Z
]
T
,
P
P
P
点在两帧图像的像素坐标系中的坐标为
p
1
p_{1}
p
1
、
p
2
p_{2}
p
2
,则有下式成立
s
1
p
1
=
KP
s
2
p
2
=
K(RP+t)
s_{1}\textbf{p}_{1}=\textbf{KP}\\ s_{2}\textbf{p}_{2}=\textbf{K(RP+t)}
s
1
p
1
=
KP
s
2
p
2
=
K(RP+t)
若采用齐次坐标,则上式可以写成
p
1
=
KP
p
2
=
K(RP+t)
\textbf{p}_{1}=\textbf{KP}\\ \textbf{p}_{2}=\textbf{K(RP+t)}
p
1
=
KP
p
2
=
K(RP+t)
取
x
1
=
K
−
1
p
1
x
2
=
K
−
1
p
2
\textbf{x}_{1}=\textbf{K}^{-1}\textbf{p}_{1}\\ \textbf{x}_{2}=\textbf{K}^{-1}\textbf{p}_{2}
x
1
=
K
−
1
p
1
x
2
=
K
−
1
p
2
此处
x
1
x_{1}
x
1
、
x
2
x_{2}
x
2
是两点在归一化平面上的坐标,代入上式可得
x
2
=
Rx
1
+
t
\textbf{x}_{2}=\textbf{Rx}_{1}+\textbf{t}
x
2
=
Rx
1
+
t
两边同时左乘
t
^
\textbf{t}\hat{}
t
^
,得到
t
^
x
2
=
t
^
Rx
1
\textbf{t}\hat{}\textbf{x}_{2}=\textbf{t}\hat{}\textbf{Rx}_{1}
t
^
x
2
=
t
^
Rx
1
两边同时左乘
x
2
T
\textbf{x}_{2}^{T}
x
2
T
,得到
x
2
T
t
^
x
2
=
x
2
T
t
^
R
x
1
x_{2}^{T}t\hat{}x_{2}=x_{2}^{T}t\hat{}Rx_{1}
x
2
T
t
^
x
2
=
x
2
T
t
^
R
x
1
因为
t
^
x
2
t\hat{}x_{2}
t
^
x
2
与
x
2
x_{2}
x
2
垂直,所以上式左侧为
0
0
0
,因此
x
2
T
t
^
R
x
1
=
0
x_{2}^{T}t \hat{} Rx_{1}=0
x
2
T
t
^
R
x
1
=
0
将
p
1
p_{1}
p
1
、
p
2
p_{2}
p
2
代入,得
p
2
T
K
−
T
t
^
R
K
−
1
p
1
=
0
p_{2}^{T}K^{-T}t \hat{} RK^{-1}p_{1}=0
p
2
T
K
−
T
t
^
R
K
−
1
p
1
=
0
上述两式被称为对极约束,它的几何意义是
O
1
O_{1}
O
1
、
O
2
O_{2}
O
2
、
P
P
P
、三点共面。对极约束中同时包含了旋转和平移,我们把中间部分基座两个矩阵:基础矩阵
F
F
F
和本质矩阵
E
E
E
E
=
t
^
R
F
=
K
−
T
E
K
−
1
E=t\hat{}R\\ F=K^{-T}EK^{-1}
E
=
t
^
R
F
=
K
−
T
E
K
−
1
则可以进一步简化对极约束
x
2
T
E
x
1
=
p
2
T
F
p
1
=
0
x_{2}^{T}Ex_{1}=p_{2}^{T}Fp_{1}=0
x
2
T
E
x
1
=
p
2
T
F
p
1
=
0
于是,相机位姿估计问题变为以下两步:
1.根据配对点的像素位置,求出
E
E
E
或者
F
F
F
;
2.根据
E
E
E
或者
F
F
F
,求出
R
R
R
,
T
T
T
。
3. 三角测量
我们使用对极几何约束估计了相机运动后,需要用相机的运动估计特征点的空间位置。仅通过单张图像无法获得像素的深度信息,我们需要通过三角测量的方法来估计地图点的深度。
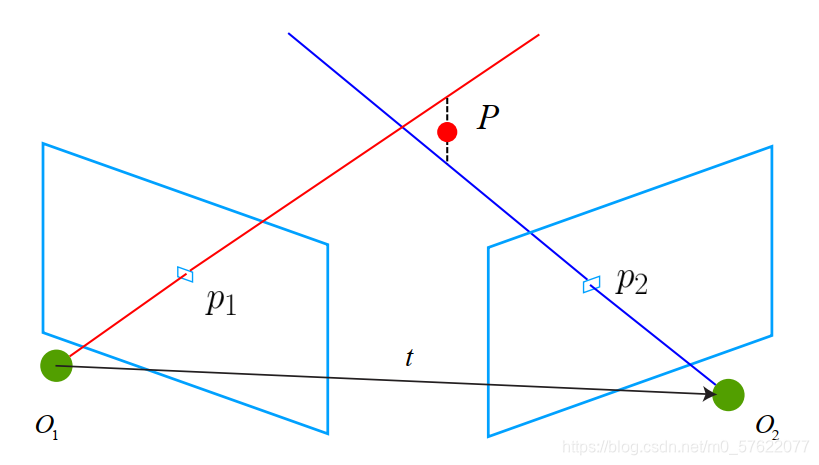
考虑图像
I
1
I_1
I
1
和
I
2
I_2
I
2
,以左图为参考,右图的变换矩阵为
T
T
T
。相机光心为
O
1
O_1
O
1
和
O
2
O_2
O
2
。
p
1
p_1
p
1
和
p
2
p_2
p
2
为两幅图像中匹配的特征点。理论上直线
O
1
p
1
O_1p_1
O
1
p
1
与
O
2
p
2
O_2p_2
O
2
p
2
在场景中会相交于点
P
P
P
,该点即是两个特征点所对应的地图点在三维场景中的位置。然而由于噪声的影响,这两条直线往往无法相交,我们可以通过最二小乘法去求解。
按照对极几何中的定义,设
x
1
x_1
x
1
,
x
2
x_2
x
2
为两个特征点的归一化坐标,那么
s
1
x
1
=
s
2
R
x
2
+
t
s_{1}x_{1}=s_{2}Rx_{2}+t
s
1
x
1
=
s
2
R
x
2
+
t
上式左乘
x
1
^
x_{1}\hat{}
x
1
^
,得
s
2
x
1
^
R
x
2
+
x
1
^
t
=
0
s_{2}x_{1}\hat{}Rx_{2}+x_{1}\hat{}t=0
s
2
x
1
^
R
x
2
+
x
1
^
t
=
0
根据此方程可以求出
s
2
s_2
s
2
。有了
s
2
s_2
s
2
,
s
1
s_1
s
1
也很容易求出。于是,我们就得到了两个帧下的点的深度,确定了它们的空间坐标。当然,由于噪声的存在,我们估得的
R
R
R
,
t
t
t
不一定精确,所以更常见的做法是求最小二乘解而不是零解。
4. 3D-2D:PnP
PnP(Perspective-n-Point)是求解 3D 到 2D 点对运动的方法。它描述了当我们知道n 个 3D 空间点以及它们的投影位置时,如何估计相机所在的位姿。
4.1 直接线性变换
考虑某个空间点
P
P
P
,它在世界坐标系下的齐次坐标为
P
=
(
X
,
Y
,
Z
,
1
)
T
\textbf{P}=(X,Y,Z,1)^{T}
P
=
(
X
,
Y
,
Z
,
1
)
T
,在归一化平面上的坐标为
x
=
(
u
,
v
,
1
)
T
\textbf{x}=(u,v,1)^{T}
x
=
(
u
,
v
,
1
)
T
。此时相机的位姿
R
,
\textbf{R},
R
,
,
t
\textbf{t}
t
是未知的。我们定义
T
=
[
R
∣
t
]
\textbf{T}=[\textbf{R}|\textbf{t}]
T
=
[
R
∣
t
]
为一个
3
×
4
3\times4
3
×
4
的矩阵,则
s
(
u
v
1
)
=
(
t
1
t
2
t
3
t
4
t
5
t
6
t
7
t
8
t
9
t
10
t
11
t
12
)
(
X
Y
Z
1
)
s\left( \begin{array}{c} u\\ v\\ 1\\ \end{array} \right) =\left( \begin{matrix} t_1& t_2& t_3& t_4\\ t_5& t_6& t_7& t_8\\ t_9& t_{10}& t_{11}& t_{12}\\ \end{matrix} \right) \left( \begin{array}{c} X\\ Y\\ Z\\ 1\\ \end{array} \right)
s
⎝
⎛
u
v
1
⎠
⎞
=
⎝
⎛
t
1
t
5
t
9
t
2
t
6
t
1
0
t
3
t
7
t
1
1
t
4
t
8
t
1
2
⎠
⎞
⎝
⎜
⎜
⎛
X
Y
Z
1
⎠
⎟
⎟
⎞
用最后一行把s消去,得到
u
=
t
1
X
+
t
2
Y
+
t
3
Z
+
t
4
t
5
X
+
t
6
Y
+
t
7
Z
+
t
8
v
=
t
5
X
+
t
6
Y
+
t
7
Z
+
t
8
t
5
X
+
t
6
Y
+
t
7
Z
+
t
8
u=\frac{t_1X+t_2Y+t_3Z+t_4}{t_5X+t_6Y+t_7Z+t_8}\\ v=\frac{t_5X+t_6Y+t_7Z+t_8}{t_5X+t_6Y+t_7Z+t_8}\\
u
=
t
5
X
+
t
6
Y
+
t
7
Z
+
t
8
t
1
X
+
t
2
Y
+
t
3
Z
+
t
4
v
=
t
5
X
+
t
6
Y
+
t
7
Z
+
t
8
t
5
X
+
t
6
Y
+
t
7
Z
+
t
8
为了简化表示,定义
T
\textbf{T}
T
的行向量为
t
1
=
(
t
1
,
t
2
,
t
3
,
t
4
)
T
t
2
=
(
t
1
,
t
2
,
t
3
,
t
4
)
T
t
3
=
(
t
1
,
t
2
,
t
3
,
t
4
)
T
\textbf{t}_\textbf{1}=\left( t_1,t_2,t_3,t_4 \right) ^T\\ \textbf{t}_\textbf{2}=\left( t_1,t_2,t_3,t_4 \right) ^T\\ \textbf{t}_\textbf{3}=\left( t_1,t_2,t_3,t_4 \right) ^T
t
1
=
(
t
1
,
t
2
,
t
3
,
t
4
)
T
t
2
=
(
t
1
,
t
2
,
t
3
,
t
4
)
T
t
3
=
(
t
1
,
t
2
,
t
3
,
t
4
)
T
则
t
1
T
P
−
t
3
T
Pu
=
0
t
2
T
P
−
t
3
T
Pv
=
0
\textbf{t}_1^T\textbf{P}-\textbf{t}_3^T\textbf{Pu}=0\\ \textbf{t}_2^T\textbf{P}-\textbf{t}_3^T\textbf{Pv}=0
t
1
T
P
−
t
3
T
Pu
=
0
t
2
T
P
−
t
3
T
Pv
=
0
可以看到每个特征点提供了两个关于
t
\textbf{t}
t
的线性约束。假设一共有
N
N
N
个特征点,可以列出如下线性方程组
(
P
1
T
0
−
u
1
P
1
T
0
P
1
T
−
v
1
P
1
T
⋮
⋮
⋮
P
N
T
0
−
u
N
P
N
T
0
P
N
T
−
u
N
P
N
T
)
(
t
1
t
2
t
3
)
=
0
\left( \begin{matrix} P_1^T& 0& -u_1P_1^T\\ 0& P_1^T& -v_1P_1^T\\ \vdots& \vdots& \vdots\\ P_N^T& 0& -u_NP_N^T\\ 0& P_N^T& -u_NP_N^T\\ \end{matrix} \right) \left( \begin{array}{c} t_1\\ t_2\\ t_3\\ \end{array} \right) =0
⎝
⎜
⎜
⎜
⎜
⎜
⎛
P
1
T
0
⋮
P
N
T
0
0
P
1
T
⋮
0
P
N
T
−
u
1
P
1
T
−
v
1
P
1
T
⋮
−
u
N
P
N
T
−
u
N
P
N
T
⎠
⎟
⎟
⎟
⎟
⎟
⎞
⎝
⎛
t
1
t
2
t
3
⎠
⎞
=
0
由于 t 一共有 12 维,因此最少通过六对匹配点,即可实现矩阵 T 的线性求解,这种方法称为直接线性变换(Direct Linear Transform,DLT)。当匹配点大于六对时,可以使用 SVD 等方法对超定方程求最小二乘解。
在 DLT 求解中,我们直接将
T
T
T
矩阵看成了12个未知数,忽略了它们之间的联系。因为旋转矩阵为正交矩阵,用 DLT 求出的解不一定满足该约束,它是一个一般矩阵。平移向量比较好办,它属于向量空间。对于旋转矩阵
R
R
R
,我们必须针对 DLT 估计的
T
T
T
的左边3 × 3 的矩阵块,寻找一个最好的旋转矩阵对它进行近似。
4.2 P3P
P
3
P
P3P
P
3
P
是另一种解
P
n
P
PnP
P
n
P
的方法。它仅使用三对匹配点,对数据要求较少。
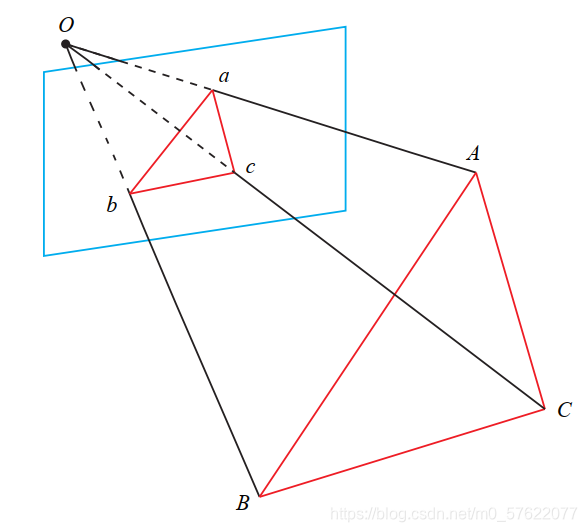
P
3
P
P3P
P
3
P
需要利用给定的三个点的几何关系。它的输入数据为三对
3
D
−
2
D
3D-2D
3
D
−
2
D
匹配点。记 3D点为
A
A
A
,
B
B
B
,
C
C
C
,2D 点为
a
a
a
,
b
b
b
,
c
c
c
,其中小写字母代表的点为大写字母在相机成像平面上的投影,如上图所示。此外,
P
3
P
P3P
P
3
P
还需要使用一对验证点,以从可能的解出选出正确的那一个(类似于对极几何情形)。记验证点对为
D
−
d
D-d
D
−
d
,相机光心为
O
O
O
。
根据余弦定理,有
O
A
2
+
O
B
2
−
2
O
A
⋅
O
B
⋅
cos
<
a
,
b
>
=
A
B
2
O
B
2
+
O
C
2
−
2
O
B
⋅
O
C
⋅
cos
<
b
,
c
>
=
B
C
2
O
C
2
+
O
A
2
−
2
O
C
⋅
O
A
⋅
cos
<
c
,
a
>
=
A
C
2
OA^2+OB^2-2OA\cdot OB\cdot \cos \left< a,b \right> =AB^2\\ OB^2+OC^2-2OB\cdot OC\cdot \cos \left< b,c \right> =BC^2\\ OC^2+OA^2-2OC\cdot OA\cdot \cos \left< c,a \right> =AC^2
O
A
2
+
O
B
2
−
2
O
A
⋅
O
B
⋅
cos
⟨
a
,
b
⟩
=
A
B
2
O
B
2
+
O
C
2
−
2
O
B
⋅
O
C
⋅
cos
⟨
b
,
c
⟩
=
B
C
2
O
C
2
+
O
A
2
−
2
O
C
⋅
O
A
⋅
cos
⟨
c
,
a
⟩
=
A
C
2
上面三式全体除以
O
C
2
OC^{2}
O
C
2
,并记
x
=
O
A
O
C
x=\frac{OA}{OC}
x
=
O
C
O
A
,
y
=
O
B
O
C
y=\frac{OB}{OC}
y
=
O
C
O
B
,可得
x
2
+
y
2
−
2
x
y
cos
<
a
,
b
>
=
A
B
2
O
C
2
y
2
+
1
−
2
y
cos
<
b
,
c
>
=
B
C
2
O
C
2
1
+
x
2
−
2
x
cos
<
c
,
a
>
=
A
C
2
O
C
2
x^2+y^2-2xy\cos \left< a,b \right> =\frac{AB^2}{OC^2}\\ y^2+1-2y\cos \left< b,c \right> =\frac{BC^2}{OC^2}\\ 1+x^2-2x\cos \left< c,a \right> =\frac{AC^2}{OC^2}
x
2
+
y
2
−
2
x
y
cos
⟨
a
,
b
⟩
=
O
C
2
A
B
2
y
2
+
1
−
2
y
cos
⟨
b
,
c
⟩
=
O
C
2
B
C
2
1
+
x
2
−
2
x
cos
⟨
c
,
a
⟩
=
O
C
2
A
C
2
记
v
=
A
B
2
O
C
2
,
u
v
=
B
C
2
O
C
2
,
w
v
=
A
C
2
O
C
2
v=\frac{AB^2}{OC^2},uv=\frac{BC^2}{OC^2},wv=\frac{AC^2}{OC^2}
v
=
O
C
2
A
B
2
,
u
v
=
O
C
2
B
C
2
,
w
v
=
O
C
2
A
C
2
,则
x
2
+
y
2
−
2
x
y
cos
<
a
,
b
>
−
v
=
0
y
2
+
1
−
2
y
cos
<
b
,
c
>
−
u
v
=
0
1
+
x
2
−
2
x
cos
<
c
,
a
>
−
w
v
=
0
x^2+y^2-2xy\cos \left< a,b \right> – v= 0\\ y^2+1-2y\cos \left< b,c \right> – uv= 0\\ 1+x^2-2x\cos \left< c,a \right> – wv= 0
x
2
+
y
2
−
2
x
y
cos
⟨
a
,
b
⟩
−
v
=
0
y
2
+
1
−
2
y
cos
⟨
b
,
c
⟩
−
u
v
=
0
1
+
x
2
−
2
x
cos
⟨
c
,
a
⟩
−
w
v
=
0
我们可以把第一个式子中的
v
v
v
放到等式一边,并代入2,3两式,可得
(
1
−
u
)
y
2
−
u
x
2
−
cos
<
b
,
c
>
y
+
2
u
x
y
cos
<
a
,
b
>
+
1
=
0
(
1
−
w
)
x
2
−
w
y
2
−
cos
<
a
,
c
>
x
+
2
w
x
y
cos
<
a
,
b
>
+
1
=
0
\left( 1-u \right) y^2-ux^2-\cos \left< b,c \right> y+2uxy\cos \left< a,b \right> +1=0\\ \left( 1-w \right) x^2-wy^2-\cos \left< a,c \right> x+2wxy\cos \left< a,b \right> +1=0
(
1
−
u
)
y
2
−
u
x
2
−
cos
⟨
b
,
c
⟩
y
+
2
u
x
y
cos
⟨
a
,
b
⟩
+
1
=
0
(
1
−
w
)
x
2
−
w
y
2
−
cos
⟨
a
,
c
⟩
x
+
2
w
x
y
cos
⟨
a
,
b
⟩
+
1
=
0
由于我们知道 2D 点的图像位置,三个余弦角是已知的。同时,
u
=
B
C
2
A
B
2
u = \frac{BC^2}{AB^2}
u
=
A
B
2
B
C
2
,
w
=
A
C
2
A
B
2
w = \frac{AC^2}{AB^2}
w
=
A
B
2
A
C
2
可以通过
A
A
A
,
B
B
B
,
C
C
C
在世界坐标系下的坐标算出,变换到相机坐标系下之后,并不改变这个比值。该式中的
x
x
x
,
y
y
y
是未知的,随着相机移动会发生变化。因此,该方程组是关于
x
x
x
,
y
y
y
的一个二元二次方程(多项式方程)。