博客

  因为要准备省赛，所以要加强对算法的学习，但是我却以这为理由，放松了对高数、线代等其他学科的学习，现在看来，这是不理智的，因为“学习都是相通的”，搞算法也要有良好的基础，而且题目也有不少直接是高数的定理、公式，所以我悔悟了，准备好好对待各个学科，从高数走起。

重积分

一、二重积分的概念和性质

  定义：二重积分是二元函数在平面区域上的积分，同定积分类似，是某种特定形式的和的极限。

  这里面的基本概念我就不一一列举了，思想是“大化小，常代变，近似和，取极限”，这个思想到后面的线面积分都会一直用到。

性质：

  1.积分可加性（满足数乘）——线性性质

  2.区域可加性（分段可加性）

  3.如果在D上，f（x，y）=1，面积为S

∫∫dxdy=∫∫dS=S

  4.如果在区域D上有f(x,y)≦g(x,y),则

              
  由于   -| f(x,y) |<=f(x,y)<=| f(x,y) |

              得


  5.
设M和m分别是函数f(x,y)在有界闭区域D上的最大值和最小值，σ为区域D的面积，

则

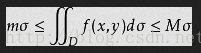
6.(二重积分的中值定理)

设函数f(x,y)在有界闭区域D上连续，σ为区域的面积，则在D上至少存在一点（ξ，η），使得

（部分公式直接从百度百科上扒的）

二、二重积分的计算法

1.利用直角坐标计算二重积分
  先x后y
  先y后x
2.利用极坐标计算二重积分
三、三重积分
  定义：略。
  性质（类比于二重积分，不再赘述）。
  计算方法：
1.利用直角坐标计算三重积分

1.“先一后二”法（思想：穿刺投影）

2..“先二后一”法（两种方法最终都是要化成三次积分法的）

2.利用柱面坐标计算三重积分

3.利用球面坐标计算三重积分

四、重积分的应用

1.曲面的面积

2.质心

3.转动惯量

4.引力

曲线积分与曲面积分

一、对弧长的积分

曲线积分分为：对弧长的曲线积分 （第一类曲线积分）

对坐标轴的曲线积分（第二类曲线积分）

两种曲线积分的区别主要在于积分元素的差别；对弧长的曲线积分的积分元素是弧长元素ds；例如：对L的曲线积分∫f(x,y)*ds 。对坐标轴的曲线积分的积分元素是坐标元素dx或dy，例如：对L’的曲线积分∫P（x,y）dx+Q(x,y)dy。但是对弧长的曲线积分由于有物理意义，通常说来都是正的，而对坐标轴的曲线积分可以根据路径的不同而取得不同的符号。(baidu baike)

被积函数是1的话，积分结果是弧长。

定积分不可看做对弧长曲线积分的特例

性质：分段可加性、对称性、轮换对称性等等。

遵循“偶零奇倍”的原则

计算方法：

二、对坐标的曲线积分

三、格林公式及其应用

四、对面积的曲面积分

五、对坐标的曲面积分

六、高斯公式

七、斯托克斯公式

（待续……