1. 特征值和特征向量

我们首先回顾下特征值和特征向量的定义如下：

Ax=λxAx=\lambda xAx=λx

其中A是一个n×nn\times nn×n的实对称矩阵，xxx是一个n维向量，则我们说λ\lambdaλ是矩阵A的一个特征值，而xxx是矩阵A的特征值λ\lambdaλ所对应的特征向量。求解特征值时，上式可以写为：

(A−λE)x=0(A-\lambda E)x=0(A−λE)x=0

从几何意义的角度，理解特征值和特征向量

首先得先弄清矩阵的概念：

一个矩阵代表的是一个线性变换规则，而一个矩阵的乘法运行代表的是一个变换。

比如有一个矩阵A：

A=(a11a21a12a22)A= \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{pmatrix}A=(a11a21a12a22)

一个列向量为x为：

x=(x1x2)x= \begin{pmatrix} x_{1} \\ x_{2} \\ \end{pmatrix}x=(x1x2)

一个矩阵的乘法为：

Ax=(a11a21a12a22)(x1x2)=(a11x1+a12x2a21x1+a22x2)=(y1y2)=YAx=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ \end{pmatrix}=\begin{pmatrix} a_{11}x_1+a_{12}x_2 \\ a_{21}x_1 +a_{22} x_2\\ \end{pmatrix} =\begin{pmatrix} y_{1} \\ y_{2} \\ \end{pmatrix}=YAx=(a11a21a12a22)(x1x2)=(a11x1+a12x2a21x1+a22x2)=(y1y2)=Y

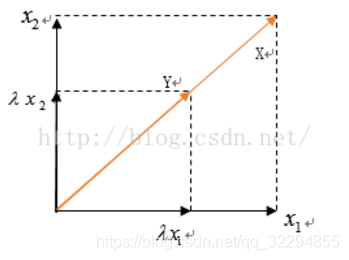
所以向量X通过矩阵A这个变化规则就可以变换为向量Y了

在几何上的变换就类似于这样：

在这里插入图片描述

知道了这个就可以从几何上理解特征值和特征向量是什么意思了，由

Ax=λxAx=\lambda xAx=λx

可知:

Ax=(a11a21a12a22)(x1x2)=(a11x1+a12x2a21x1+a22x2)=(λx1λx2)=YAx=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ \end{pmatrix}=\begin{pmatrix} a_{11}x_1+a_{12}x_2 \\ a_{21}x_1 +a_{22} x_2\\ \end{pmatrix} =\begin{pmatrix} \lambda x_{1} \\ \lambda x_{2} \\ \end{pmatrix}=YAx=(a11a21a12a22)(x1x2)=(a11x1+a12x2a21x1+a22x2)=(λx1λx2)=Y

所以，确定了特征值之后，向量x的变换为：

方向没有改变！！！

在这里插入图片描述

引用《线性代数的几何意义》的描述：“

矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中，原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值

”。对于实对称矩阵来说，不同特征值对应的特征向量必定正交;我们也可以说，一个变换矩阵的所有特征向量组成了这个变换矩阵的一组基。

那么这样定义的特征值和特征向量有什么实际用途呢?在这里我举个数据挖掘算法中重要的一个算法：PCA（主成分分析）来给大家直观的感受一下。

2. 在PCA中应用

首先，理解一下信息量这个概念

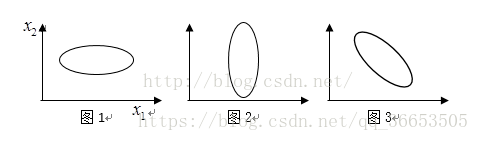
看几张图：

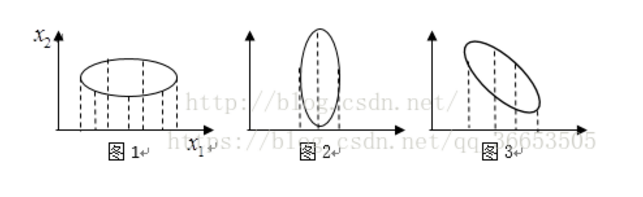
在这里插入图片描述

如果我们单独看某一个维度的话，比如看x1这个维度:

可以看到将点投影到x1这个维度上看的话，图1的数据离散性最高，图3较低，图2数据离散性是最低的。数据离散性越大，代表数据在所投影的维度上具有越高的区分度，这个区分度就是信息量。如果我们用方差来形容数据的离散性的话，就是数据方差越大，表示数据的区分度越高，也就是蕴含的信息量是越大的。

基于这个知识，如果我们想对数据进行降维的话，比如图1的两个维度的数据降成一维，我们可以选择保留X1这个维度的数据，因为在这个维度上蕴含的信息量更多。

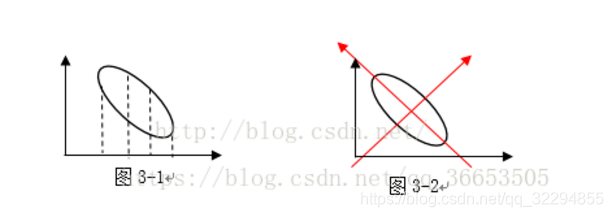
同理，图2就可以保留x2这个维度的数据。但是，问题来了，图3应该保留哪个维度的数据呢？答案是保留哪个维度(x1或x2)都不好，都会丢失较大的信息量。但是，如果我们把图3的坐标轴旋转一下

在这里插入图片描述

比较容易看出，图3在新的坐标轴下就能进行降维了。所以选取正确的坐标轴，然后根据各个维度上的数据方差大小，决定保留哪些维度的数据，这样的做法就是主成分分析的核心思想。

选取正确的坐标轴的过程中，我们需要一个矩阵变换，就类似于这样：

在这里插入图片描述

其实，经过数学上的推导的，我们就可以知道，特征值对应的特征向量就是理想中想取得正确的坐标轴，而特征值就等于数据在旋转之后的坐标上对应维度上的方差。

也就是说，直接求出矩阵A的特征向量得出对应的特征向量。我们就能找到旋转后正确的坐标轴。这个就是特征值和特征向量的一个实际应用：“得出使数据在各个维度区分度达到最大的坐标轴。”

所以，在数据挖掘中，就会直接用特征值来描述对应特征向量方向上包含的信息量，而某一特征值除以所有特征值的和的值就为：该特征向量的方差贡献率（方差贡献率代表了该维度下蕴含的信息量的比例）。