gs1:
ch0:
均匀变化: s=v*(b-a)
非均匀变化:
1) 分 2)均 3)合 4)精
微积分研究的主要对象:
函数y=f(x) (a<=x<=b)的变化规律
微观(变化率) 宏观(改变量)
微积分研究的思想方法:
利用已知求未知
均匀变化 非均匀变化
局部均匀化求近似,利用极限得精确
导数与积分的本质:
导数和积分分别处理均匀量的商和积在处理非均匀量中的发展
ch1:函数 极限 连续
sec1:函数
函数概念: 每个x有唯一确定的y按照一定法则一一对应
(1)符号函数y=sgn x
(2)取整函数,记为[x]:不超过x的最大整数
(3)复合函数:y=f(u),u=g(x).内层函数u的值域和外层函数f的定义域交集不为空集
(4)反函数:任意y属于R,有唯一确定的x属于D,使得y=f(x),则记为x=f^(-1) (y),称其为y=f(x)的反函数 y=x^2没有反函数。严格单调函数一定有反函数,反之则不然。函数有反函数的充要条件:一一映射
有时,将 y=f(x)的反函数x=f-1(y)写成y=f-1(x)
在同一直角坐标系中,y=f(x) ,和x=f-1(y)的图形重合,和y=f-1(x)的图形关于直线y=x对称。
f-1[f(x)]=x
(5)初等函数:
基本初等函数:幂指对三反
初等函数:由常数和基本初等函数加减乘除复合组成的函数
函数性质:
(1)单调性
(2)奇偶性:
奇函数:sinx,tanx,arcsinx,arctanx,x,ln[(1-x)/(1+x)],ln(x+(1+x^2)^(1/2),(e^x-1)/(e^x+1),f(x)-f(-x)
偶函数:x^2,cosx,f(x)+f(-x)
奇函数图形关于原点对称且f(0)=0;偶函数关于y轴对称。
(3)周期性:
f(x+T)=f(x).
f(ax+b) 以T/|a|为周期
(4)有界性:
存在M>0,使得任意x属于X,恒有|f(x)|<=M,则称f(x)在X上为有界函数
sec2:极限
题型一:极限的概念性质及存在准则(选择证明)
题型二:求极限(计算填空)
题型三:无穷小量阶的比较
(一)极限的概念
1.数列的极限
4个考点
n->∞,xn->a;
N是分割前面N个有限项和N后面无限个项,并使N后面无限个项落在xn的邻域内
数列{xn}的极限与前有限项无关
n,k->∞,limxn=a <=> limx2k-1=limx2k=a(奇数列等于偶数列的极限等于a<=>数列极限等于a)
2.函数的极限
(1)自变量趋于无穷大时函数的极限
经典错误:x->oo,(x^2+1)^(1/2)/x的极限不存在,而不是等于1.(video2)
x->oo <=> |x|->+oo.
f()的函数极限存在=》数列极限存在
(2)自变量趋于有限值时函数的极限
【注】1)任意性,x-》x0,但x!=x0。
x->x0,f(x)->A.
lim(x->x0) f(x)
与
f(x0)
无关
所以极限 x->x0,但x!=x0.
经典错误:
x->0,sin(x*sin(1/x))/x*sin(1/x)!=1,
极限不存在
.
原因:因为有数列x(n) = 1/(nπ),n = 1, 2, …;x(n) → 0 (n→∞),使得函数f(x) = sin[x*sin(1/x)]/[x*sin(1/x)]在 x(n) 没定义,即极限lim(n→∞)f[x(n)]不存在,因此极限 lim(x→0)f(x)不存在.
(3)左、右极限
左右极限存在且相等才能推出函数极限存在
分左、右极限求极限的问题有三种:
(1)分段函数在分界点处的极限
(2)e^oo型极限
(3)arctanoo型极限(如x->0,arctan1/x;)
(二)极限性质
1.有界性:
(1)(数列)如果数列{xn}收敛,那么数列{xn}一定有界。
有界不能推收敛:经典反例an=(-1)^n.
(2)(函数)如果lim(x->x0)f(x)存在,则f(x)在x0某去心邻域有界(即局部有界)。
f(x)
局部有界不能推
lim(x->x0)f(x)
存在:经典范例
lim[x->x0]sin(1/x)
振荡。
x->0
时,它去心邻域的函数值在
[-1,1]
,但是它不存在。
2.保号性:
(1)数列 :设lim[n->oo]xn=A
(1)如果A>0(或A<0),则存在n>N时,xn>0(或xn<0);
(2) 如果存在N>0,当n>N时,xn>=0(或xn<=0),则A>=0(或A<=0)。
n->+∞
,
A>0 => xn>0;
xn>=0 => A>=0;
A>=0
不能推
xn>=0:
经典反例
[
(
-1
)
^n]/n->0;
xn>0
不能推
A>0:
经典反例
1/n->0;
(2)函数:设lim[n->oo]f(x)=A
(1)
已知极限大于或小于
0
:
A>0 => f(x)>0;
(2)
已知函数大于等于或小于等于
0
:
f(x)>=0 => A>=0;
排除法:
(1)何时用:出现一般函数
(2)如何用:套具体函数
3.极限值与无穷小之间的关系:
limf(x)=A <=> f(x)=A+a(x) 其中 lima(x)=0
(三)极限存在准则
(1)夹逼准则:(n项和的极限)
(2)单调有界准则:(递推关系xn+1 = f(xn):(1)单调有界准则证极限存在;(2)a=f(a)=>a; )
单调有界数列必有极限:
单调增有上界的数列必有极限;
单调减有下界的数列必有极限;
(四)无穷小量
(1)无穷小量的概念
(2)无穷小的比较:
(1)高阶:
(2)低阶:
(3)同阶:
(4)等价:
(5)无穷小的阶:
(3)无穷小的性质:
(1)有限个无穷小的和仍是无穷小;(√)
——无穷小的和仍是无穷小(×)经典反例n->oo时,n项无穷小的和lim[n->+oo] [1/n^2+2/n^2+……+n/n^2]=1/2 != 0;
(2)有限个无穷小的积仍是无穷小;经典错误:lim[x->0] xsin1/x=(lim[x->0] x)( lim[x->0] sini/x);后面()的极限不存在;乘积的极限拆分时必须保证拆分项的极限存在。
(3)无穷小与有界量的积仍是无穷小;
(五)无穷大量
(1)无穷大量的概念:
(2)常用的一些无穷大量的比较:
当x->+oo时,(lnx)^a<<x^B<<a^x,其中a>0,B>0,a>1
当n->oo时,(lnn)^a<<n^B<<a^n<<n!<<n^n,其中a>0,B>0,a>1;
(3)无穷大量的性质:
无穷大+无穷大不一定等于无穷大:经典反例(n)+(-n)=0
无穷大×有界不一定等于无穷大:经典反例(n×1/n^2=1/n)
无穷小×有界=无穷小
(1)有限个无穷大量的积仍为无穷大量;
(2)无穷大量与有界变量之和仍为无穷大量;
(4)无穷大量与无界变量的关系:
(1)数列{xn}是无穷大量:
N项以后的值都比M大;
(2)数列{xn}是无界变量:
有那么一项xN的值比M大;
最终得出结论:无穷大量 => 无界变量:例子:奇数项为n,偶数项为0:1,0,3,0,5,0,……,2n-1,0,……:是无界变量但不是无穷大量;
(5)无穷大量与无穷小量的关系:
1/无穷大=无穷小(√)
1/无穷小=无穷大(×)
f(x)是无穷小且f(x)!=0,则1/f(x)是无穷大。(√)
sec3:
(一)极限的概念、性质及存在准则
|xn-a|<?是|xn-a|<=2?的充要条件;
一个数列有极限,这个数列的任何部分项都有极限:数列有极限<=>数列的奇数项和偶数项的极限存在且相等
(二)求极限——常用的求极限方法(8种)
(1)利用基本极限求极限
(1)常用的基本极限:
lim(x->0) sinx/x=1,lim(x->0) (1+x)^1/x=e,lim(x->oo) (1+1/x)^x=e等;多项式之比,x->oo看幂的最高次,x–>0,看幂的最低次;
(2)1^oo型极限常用结论:
若lima(x)=0,limb(x)=oo,且lima(x)b(x)=A,则lim[1+a(x)]^b(x)=e^A;
lim[n->oo] (n^n)/(n+1)^n=1,(×);
(2)利用等价无穷小代换求极限
(1)代换原则
a)乘除关系可以换
若a~a1,b~b1,则lim a/b=lim a1/b =lim a/b1 =lim a1/b1;
b)加减关系在一定条件下可以换
若a~a1,b~b1,且 lim a1/b1=A !=1,则a-b~a1-b1;(两个减项不等价可以换,先换后验)lim (a-b)/(a1-b1)=lim b[a/b-1]/b1[a1/b1-1]=1;
若a~a1,b~b1,且 lim a1/b1=A !=-1,则a+b~a1+b1;(两个加项之比极限不等于-1可以换,先换后验)
(2)常用的等价无穷小:当x->0时,
(1)x-sinx~x^3/6, (2)tanx-x~x^3/3, (3)x-ln(1+x)~x^2/2等;
(1)商存在,分母趋向0,则分子一定趋向0;
@(2)当x->0时,(1+x)^a-1~ax可推广为:若a(x)->0,a(x)b(x)->0,则(1+a(x))^b(x)-1~a(x)b(x);
(3)利用有理运算法则求极限
(1)有理运算法则:
两个极限存在,则这两个极限的和差积商一定存在,为商时分母的极限不为0;
【注】(1)存在+-不存在=不存在;
(2)不存在+-不存在=不一定;n+n=不存在,n+(-n)=存在;
(3)存在×÷不存在=不一定;1×n=不存在,1/n×n=存在;
(4)不存在×÷不存在=不一定;(-1)^n ×(-1)^n=存在;
极限,连续,导数,无穷级数,该结论相同。
常用的结论:(1)极限的非零的因子的极限可先求出来:limf(x)=A != 0 =>limf(x)g(x)=Alimg(x);
经典反例:lim[x->0] ( e^(x^2)*cosx-1 )/x^2=lim[x->0] ( e^(x^2)-1 )/x^2=1是错的!
(2)lim f(x)/g(x)存在,lim g(x)=. 0 => lim f(x) = 0:
证明:【经典错误】如果lim f(x) !=0,而又因为lim g(x)=.0,这与lim f(x)/g(x)存在相矛盾,故lim f(x) =0;原因:只证明了lim f(x)存在非0不成立,但lim f(x)也可以不存在;(不存在×÷存在=不一定)
【正确证明】因为lim f(x)/g(x)存在,又因为lim g(x)= 0,所以lim f(x)/g(x) * lim g(x)存在且等于0,所以lim f(x)=0;
(3)lim f(x)/g(x) = A !=0,lim f(x)=0 => lim g(x)=0;
如果A != 反例:lim [x->0] 2x/(1+x^2] =0,分母极限就不等于0;
证明:因为lim f(x)/g(x) = A !=0,所以lim f(x)/[f(x)/g(x)]=0,所以lim g(x) =0;
(4)利用洛必达法则求极限
若(1)lim[x->x0] f(x)=lim[x->x0] g(x)=0或者∞; 0/0,∞/∞;
(2)f(x)和g(x)在x0的某去心邻域内可导,且g'(x)!=0;
(3)lim[x->x0] f'(x)/g'(x)存在(或∞);
则 lim[x->x0] f(x)/g(x)=lim[x->x0] f'(x)/g'(x). 存在
【注】(1)适用类型:0/0; ∞/∞; 0*∞; ∞-∞; 1^∞; ∞^0; 0^0。
1^∞,∞^0,0^0 => 0*∞ => 0/0 , ∞/∞
∞-∞ => 0/0 , ∞/∞
[f(x)]^g(x)=e^(g(x)ln(x))——0*∞;——∞^0; 0^0
1^∞=(1+a)^b; ab->A; 原式=e^A;
化简:(1)等价代换(2)lim f(x)=A (3) 有理化
【经典错误】设f(x)二阶可导,f(0)=0,f'(0)=1,f”(0)=2.求极限lim[x->0] (f(x)-x)/x^2.
原式 ?= lim[x->0] (f'(x)-1)/2x != lim[x->0] f”(x)/2 != f”(0)/2=1。原因是:(1) 无法判断等号后面的极限limf'(x)存在不存在或为∞ (2) 二阶可导不能保证二阶导数有极限;(3) f”(x)无法判断是否连续,所以f”(x)的极限!=f(0)。
【结论】(1)f(x) n阶可导,洛必达法则最多使用到f(x)的(n-1)阶导
(2)f(x)有n阶连续导数,洛必达法则最多使用到f(x)的n阶导
正确解:(1)lim[x->0] (f(x)-x)/x^2=lim[x->0] (f'(x)-1)/2x =1/2 *lim[x->0] (f'(x)-f'(0))/x =f”(0)/2=1。(导数定义)
(2)泰勒公式
(5)利用泰勒公式求极限
求极限往往用佩亚诺余项的泰勒公式,俗称局部泰勒公式。
原则:上下同阶原则
(6)利用夹逼原理求极限
n项和的题:放缩,夹逼
n次根式的题:lim[n->∞] x^n=0 ,|x|<1;
lim [n->∞] n#(1^n+2^n+3^n)=3;夹逼:n#(3*3^n)>原式>n#(3^n) ,所以等于3.


(7)利用单调有界准则求极限
递推关系的题:单调有界证存在;令极限=a求a。
(1)2ab<=a^2+b^2.
(2)(abc)^(1/3)<=(a+b+c)/3
为什么要证极限存在?反例:x1=1,x(n+1)=1-xn,则数列为1,0,1,0,1,……,1,0……极限不存在
(8)利用定积分定义求极限
lim[n->∞] [1/(n+1) + 1/(n+2) +……+1/(2n)]=ln2
求n项和的题:先提可爱因子1/n。
(1)sinx<x<tanx,0<x<pi/2;
(2)x/(1+x)<tan(1+x)<x,x>0;
(三)函数的连续性
常考题型与典型例题:
题型一 讨论函数连续性及间断点的类型*
题型二 有关闭区间上连续函数性质的证明题
sec1:连续性的概念
定义1 略
定义2 若lim[x->x0] f(x)=f(x0),则函数在x0处连续——在某一点x0上:极限存在,函数有意义,极限与函数相等。
定义3:左连续,右连续
定理:f(x)连续 <=> f(x)左连续且右连续
定义4:区间上的连续:(1)开区间:求某一点连续 (2)闭区间:求某一点连续再求端点处左右连续
sec2:间断点及其分类
不连续的点就叫间断点(×) 反例:lnx 在x=-1
(1)间断点的定义:
定义5 若f(x)在x0某去心邻域有定义,但在x0处不连续,则称x0为f(x)的间断点。
——x0点可以没定义,但起码它的邻域得有定义。
(2)间断点的分类(第一类间断点要说明具体是哪一种间断点,第二类间断点没有特殊要求不用说明)
(1)第一类间断点:左右极限均存在的间断点
可去间断点 左极限=右极限
跳跃间断点:左极限!=右极限
(2)第二类间断点:左、右极限中至少有一个不存在
无穷间断点 lim[x->0] 1/x=无穷
振荡间断点 lim[x->0] sin(1/x)不存在
分段函数分界点,e^∞,arctan∞分左右,其他的情况一般不用分左右。
(ln|x|)’=1/x; lim [x->0+] (x^a)lnx=0 (a>0); f(x)->0 <=> |f(x)|->0;
sec3:连续性的运算与性质
定理1 连续函数的和差积商(分母不为零)仍为连续函数;
定理2 连续函数的复合仍为连续函数;
定理3 基本初等函数在其定义域内是连续的;
定理4 初等函数在其定义区间内是连续;*
例子:f(x)=1/x,x!=0是f(x)的定义域,包含在定义域内部的区间都叫定义区间。
反例: f(x)=(cosx-1)^(1/2),只在2npi上有定义,定义域就是这些离散的点,被包含在这个函数定义域内部的区间没有。
sec4:闭区间上连续函数的性质
定理5 (有界性定理)
有限闭区间上连续的函数,在这个闭区间上一定有界;
定理6 (最值定理)
有限闭区间上连续的函数,在这个闭区间上一定有最大值、最小值;
定理7(介值定理)
若f(x)在[a,b]上连续,且f(a)!=f(b),则对f(a)与f(b)之间任一数C,至少存在一个₰∈(a,b),使得f(₰)=C;
推论:若f(x)在[a,b]上连续,则f(x)在[a,b]上可取到介于它在[a,b]上最小值与最大值之间的一切值。
定理8 (零点定理)
若f(x)在[a,b]上连续,且f(a)*f(b)<0,则必存在₰∈(a,b)使得f(₰)=0;
解:由于f(x)是初等函数,则除x=0,x=1外处处连续。原因:x=0,x=1处是没有定义的点,其他的点都在定义区间内,由定理4 初等函数在其定义区间内是连续的,所以f(x)在其他点处是连续的。
基本初等函数有定义就连续,初等函数有定义区间就连续。
lim x^n: 当|x|<1,lim x^n=0;
当|x|>1,lim x^n=∞;
当|x|=1,lim x^n=1;
当|x|=-1,lim x^n=不存在;
【总结】1.函数:(1)复合 (2)性质
2.极限:(1)概念、性质、准则 (2)求极限* (3)无穷小比阶*
3.连续:(2)间断点及其类型 *(2)性质
(三)高阶导数
(1)定义6(高阶导数)
【注】如果f(x)在点x处n阶可导,则在点x的某邻域内f(x)必定具有一切低于n阶的导数。
(2)常用的高阶导数公式:
(sinx)^(‘n)=sin(x+n*pi/2); (cosx)^(‘n)=cos(x+n*pi/2); (uv)^(‘n)=略;
(sinax)^(‘n)=(a^n)*sin(ax+n*pi/2);
【常考题型与典型例题】
1.导数定义;2.复合函数、隐函数、参数方程求导;3、高阶导数;4、导数应用
1.导数定义:
凑导数定义的形式(拆项):知f'(x0)值,求某式子的极限。也可以用具体函数法。
直接法,排除法:遇到一般函数用具体函数替换挨个排除项。


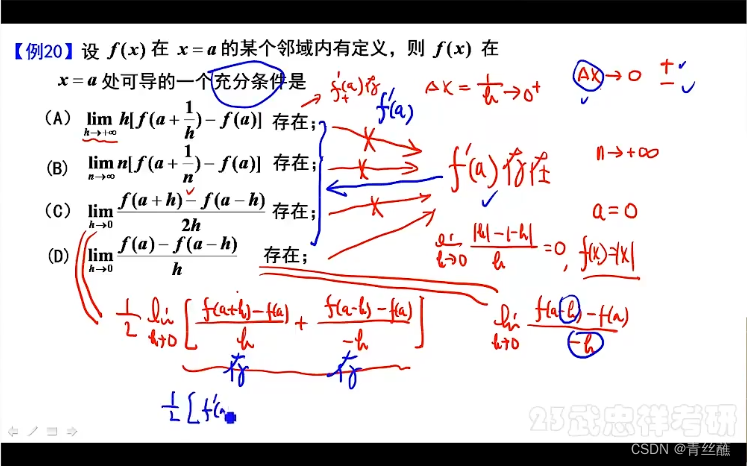
【经典错误】lim[h->0] [f(a+h)-f(a-h)]/2h=(1/2)*lim[h->0] {[f(a+h)-f(a)]/h + [f(a-h)-(a)]/(-h)} 推出A或B存在。其中A=[f(a+h)-f(a)]/h,B=[f(a-h)-(a)]/(-h);(×) 原因:A、B相加有极限并不能推出A或B有极限。
2.复合函数、隐函数、参数方程求导:

3.高阶导数
(1)公式
(2)求y’,y”,再归纳y^(‘n).
(3)泰勒公式:求哪点写哪一点的泰勒公式。

(四)导数应用
(1)导数的几何意义
求切线,求法线。
(2)相关变化率
已知x对t的变化率是v0,求l在(0,0)点对t的变化率:
(1)建立l与x的关系;
(2)dl/dt=(dl/dx)*(dx/dt)=(dl/dx)*v0.
ch3:微分中值定理及导数应用:
题型一 求极限
题型二 函数的极值和最值,曲线的凹向与拐点
(一)微分中值定理
费马(某点可导且在某点取极值,一定有f'(x0)=0 )——>罗尔(区间连续+端点的函数值相等+区间内可导=f(x)在区间内一定有一点取极值)——>拉格朗日(曲线上存在切线平行于端点弦)——>柯西(y=f(x)变为参数方程y=y(t),x=x(t));
定理1 (费马引理)
如果函数f(x)在x0处可导,且在x0处取得极值,那么f'(x0)=0; 两个条件缺一个的反例f(x)=|x|;
函数与函数的一阶导
定理2 罗尔定理:*
定理3 拉格朗日中值定理:
f(b)=f(a)便是罗尔定理
定理4 柯西中值定理
分母的F(x)=x,便是拉格朗日中值定理
函数与函数的高阶导
定理5 皮亚诺型余项泰勒公式 局部:极限,极值
n阶可导
f(x)=f(x0)+f'(x0)(x-x0)+………….
若x=0,则为麦克劳林公式。
定理6 拉格朗日型余项泰勒公式 整体:最值、不等式
(n+1)阶可导
泰勒公式共同点:(1)多项式逼近 一般函数(2)函数与高阶导的关系
不同点:(1)条件不同(2)余项不同
(二)导数应用
1.函数的单调性
f(x)在闭区间连续在开区间内可导,若导数大于0,f(x)在区间内单调增;若导数小于0,f(x)在区间内单调减。
2.函数的极值
定义:
区间内恒有f'(x)>=f(x0),称f(x)在x0取极小值。
区间内恒有f'(x)<=f(x0),称f(x)在x0取极大值。、
定理8 极值的必要条件
f(x)在x0处可导且在x0点取得极值,则f'(x0)=0;
函数极值点一定是驻点(错):反例f(x)=|x|;
可导函数极值点一定是驻点。(对)
可能的极值点:(1) f'(x0)=0 (2) f'(x0)不存在
定理9 极值的第一充分条件:导数在x0的两侧发生变号
定理10 极值的第二充分条件:一阶导等于0,二阶导不等于0:二阶导小于0取极大,二阶导大于0取极小。
3.函数的最大最小值
(1)求连续函数f(x)在[a,b]上的最值
step1:求出在(a,b)内的驻点和不可导点
step2:求出驻点和不可导点以及端点的函数值
step3:比较以上各点的函数值
(2)最大最小值的应用题
step1:建立目标函数
step2:三部曲
4.曲线的凹凸性
定义3:
凹: f[(x1+x2)/2]<[f(x1)+f(x2)]/2;
凸: f[(x1+x2)/2]>[f(x1)+f(x2)]/2;
定理11 若在区间I上f”(x)>0(<0),则曲线y=f(x)在I上是凹(凸)的。
定义4(拐点) 拐点是坐标。(你可以说x=x0是极值点但不可以说x=x0是拐点。
判定(必要条件与充分条件)极点的一个必要两个充分抬高一阶
5.曲线的渐进线
(1)水平渐近线lim[x->∞] f(x)=A,y=A是水平渐近线。一条曲线最多两条水平渐近线im[x->+∞] f(x)=A,或im[x->-∞] f(x)=A。如y=arctanx;
(2)垂直渐近线im[x->x0] f(x)=∞,那么x=x0是y=f(x)的垂直渐近线。
(3)斜渐近线 lim[x->∞] f(x)/x=a,b=lim[x->∞] (f(x)-ax),那么y=ax+b是y=f(x)的斜渐近线。最多两条x趋向±∞时,取a和b不完全相同。
【注】在+∞或-∞这一侧,有水平渐近线就没有斜渐近线,有斜渐近线就没有水平渐近线。
有水平渐近线就没有斜渐近线,有斜渐近线就没有水平渐近线。(×)反例:可以负无穷有水平渐近线,正无穷有斜渐近线。
6.函数的作图
7.曲线的弧微分与曲率
曲率 K=|y”|/(1+y’²)^(3/2)
曲率半径R=1/K;
常考题型与典型例题
1.求函数的极值与最值,确定曲线的凹向和拐点:
保号性、极值定义;排除法
【注】分段函数的分段点处存在左右导数不相等即不可导的情况,需要先求左右导数进行判断。之后再决定分段函数求导时要不要加入分段点。但最后还是要讨论分段点是不是极值点((1)在分段点,函数是否连续,导数是否变号(2)极值点的定义)。
应用题:(1)建立目标函数(2)找极值点三步走:求导数,找驻点,再判定
建立目标函数不唯一,找最好求导的目标函数。
拐点:找二阶导为0和不存在的点。再判断左右二阶导是否变号。不存在的点左右二阶导变号还要判定一阶导在这一点是否连续

2.求渐近线;


3.方程的根:
(1)存在性:
零点定理:f(a)f(b)<0;
罗尔定理:找函数f(x)的原函数,然后用罗尔使f(x)=0;
(2)个数:
单调性
4.不等式的证明:
(1)拉格朗日定理

(2)单调性


5.中值定理证明题

下图用到介值定理:

ch4:不定积分:
1.不定积分的概念与性质
1.原函数 F'(x)=f(x)
2.不定积分 ∫f(x)dx = F(x)+C
3.不定积分的几何意义
4.原函数存在定理:
定理1:若f(x)在区间I上连续,则f(x)在区间I上一定存在原函数。
定理2:若f(x)在区间I上有第一类间断点,则f(x)在区间I上没有原函数。例子:g(x)=sgn(x);
5.不定积分的性质:
(1)积分的导数=被积函数; 积分的微分=被积函数*dx
(2)导数的积分=被积函数+C;微分的积分=被积函数+C;
(3)和差的积分=积分的和差;【分项积分法】
(4)常数×f(x)的不定积分=f(x)的不定积分×常数;
2.不定积分的基本公式
略。
【应用】分项积分法
3.三种主要积分法
+-:分项积分法(加项减项拆)
×÷:分部积分法
复合:换元法
(1)第一类换元法:凑微分:dx/x=d(lnx+C) ; dx/√x=2d√x ;
(2)第二类换元法:
定理:略
常用的换元:
三角代换: 去根号
√(a²-x²) x=asint或者acost
√(a²+x²) x=atant
√(x²-a²) x=asect
(3)分部积分
∫udv=uv-∫vdu 适用两类不同函数相乘
原则:
1.遇到对数或反三角,对数反三角以外的函数凑微分
2.遇到幂,幂以外的函数凑微分
3.遇到指数或三角,指数三角以外的凑微分
(4)有原函数但不可积的函数
(1)∫e^(x²)dx
(2)∫(sinx/x) dx
(3)∫(cosx/x) dx
4.三类常见可积函数积分
(1)有理函数积分 ∫R(x)dx
(1)一般法(部分分式法):分母因子的重数=该因子拆成分式的项数,分母因子的最高次数=拆成项分子的最高次数
*(2)特殊方法(加项减项拆或凑微分降幂);
(2)三角有理式积分: ∫R(sinx,cosx)dx
(1)一般方法(万能代换 ) 令tan(x/2)=t
∫R(sinx,cosx)dx = ∫R[ 2t/(1+t²) , (1-t²)/(1+t²) ] *[2/(1+t²)]dt
*(2)特殊方法(三角变形,换元,分部)
(1)若R(-sinx,cosx)=-R(sinx,cosx),则令u=cosx dcosx
(2)若R(sinx,-cosx)=-R(sinx,cosx),则令u=sinx dsinx
(3)若R(-sinx,-cosx)=R(sinx,cosx),则令u=tanx dtanx
换元后加项减项拆
(3)简单无理函数积分 ∫R{ x, [(ax+b)/(cx+d)]^(1/n)}dx
*一般方法:令[(ax+b)/(cx+d)]^(1/n)=t;
2+3+3:2个概念,*3种方法,3类积分
常考题型与典型例题
求不定积分(换元、分部)
被积函数f(x)是连续的分段函数,只要证明它的原函数在分段点处是连续的,那么它在分段点处一定也可导. 【被积函数是连续的分段函数,做不定积要分段做,做完以后要调整任意常数,只要保证它在分段点处连续,那么自然保证它在分界点可导,导数等于被积函数。




ch5:定积分:
题型一 定积分的概念、性质及几何意义
题型二 定积分的计算
题型三 变上限定积分
1.定积分概念
(1) 定积分的定义 【分 匀 和 精】

(2)定积分存在的
充分条件
:
(1)f(x)在[a,b]上连续;
(2)f(x)在[a,b]上
有界且只有有限个间断点
;
(3)f(x)在[a,b]上
仅有有限个第一类间断点;
【注】可积函数一定有界,但有界函数不一定可积; 反例:狄雷克力函数:D(x)={有理:=1 ;无理: = 0;}
(3)f(x)>0 ,f(x)的定积分等于曲线与区间围成的面积;
f(x)<0 ,f(x)的定积分等于曲线与区间围成的面积的负值;
f(x)可正可负, f(x)的定积分等于上面的面积减去下面的面积;
2.定积分的性质
(1)不等式:
(1)若f(x)<=g(x),则f(x)在区间[a,b]的积分<=g(x)在区间[a,b]的积分,其中a<b;
(2)f(x)在区间[a,b]上连续,则m(b-a)<=f(x)在区间[a,b]的积分<=M(b-a),m和M分别是f(x)在区间的最小值和最大值;
(3)积分的绝对值<=绝对值的积分;
(2)中值定理:
*(1)若f(x)在[a,b]上连续,则∫【a,b】f(x)dx=f(&)(b-a);a<&<b;
(2)
若
f(x)
,
g(x)
在
[a,b]
上连续
,g(x
)不变号,则∫【
a,b
】
f(x)g(x)dx=f(&)
∫【
a,b
】
g(x)dx,a<=&<=b;
3.积分上限的函数*
∫【a,x】f(t)dt=F(x);
定理: 若f(x)在[a,b]上连续,则∫【a,x】f(t)dt在[a,b]上可导且(∫【a,x】f(t)dt)’=f(x).
【揭示了微分和积分的内在联系是逆运算,揭示了原函数的存在性——连续函数一定有原函数。】
定理: 设f(x)连续
(1)若f(x)是奇函数,则∫【0,x】f(t)dt是偶函数;
(2)若f(x)是偶函数,则∫【0,x】f(t)dt是奇函数;
4.定积分的计算*
(1)牛顿-莱布尼茨公式
(2)换元法
(3)分部积分法
(4)利用奇偶性、周期性
(5)利用公式
华里士公式等公式



题型一 定积分的概念、性质及几何意义
题型二 定积分的计算
第一步,奇偶性化简
第二步,
(1)定积分的几何意义算积分:
∫【0,a】√(a²-x²)= pi*a²/4;(a>0);
∫【0,a】√(2ax-x²)= pi*a²/4;(a>0);
∫【0,2a】√(2ax-x²)= pi*a²/2;(a>0);
(2)
∫【0,pi】xf(sinx)dx=(pi/2)∫【0,pi】f(sinx)dx

题型三 变上限定积分
(1)上下限有x被积函数没有x——直接求导
(2)上下限与被积函数都有x——加项减项拆或作变量代换化成第一种形式再求导
(3)抽象函数的积分中抽象函数里既有x又有t——变量代换

求导带值:F(x)在x=pi处连续,那么0<=x<pi可以写成0<=x<=pi,左导右导都可以求导带值,就不需要麻烦的用定义求左右导数来做了。

定积分出现在极限中,


(积分中值定理第二个,让值不为0的做f(x);)
sec2:反常积分
(1)无穷区间上的反常积分
定义1:∫【a,+∞】f(x)dx=lim【t->+∞】∫【a,t】f(x)dx
定义2:∫【-∞,b】f(x)dx=lim【t->-∞】∫【t,b】f(x)dx
定义3:∫【-∞,+∞】f(x)dx=∫【-∞,0】f(x)dx + ∫【0,+∞】f(x)dx

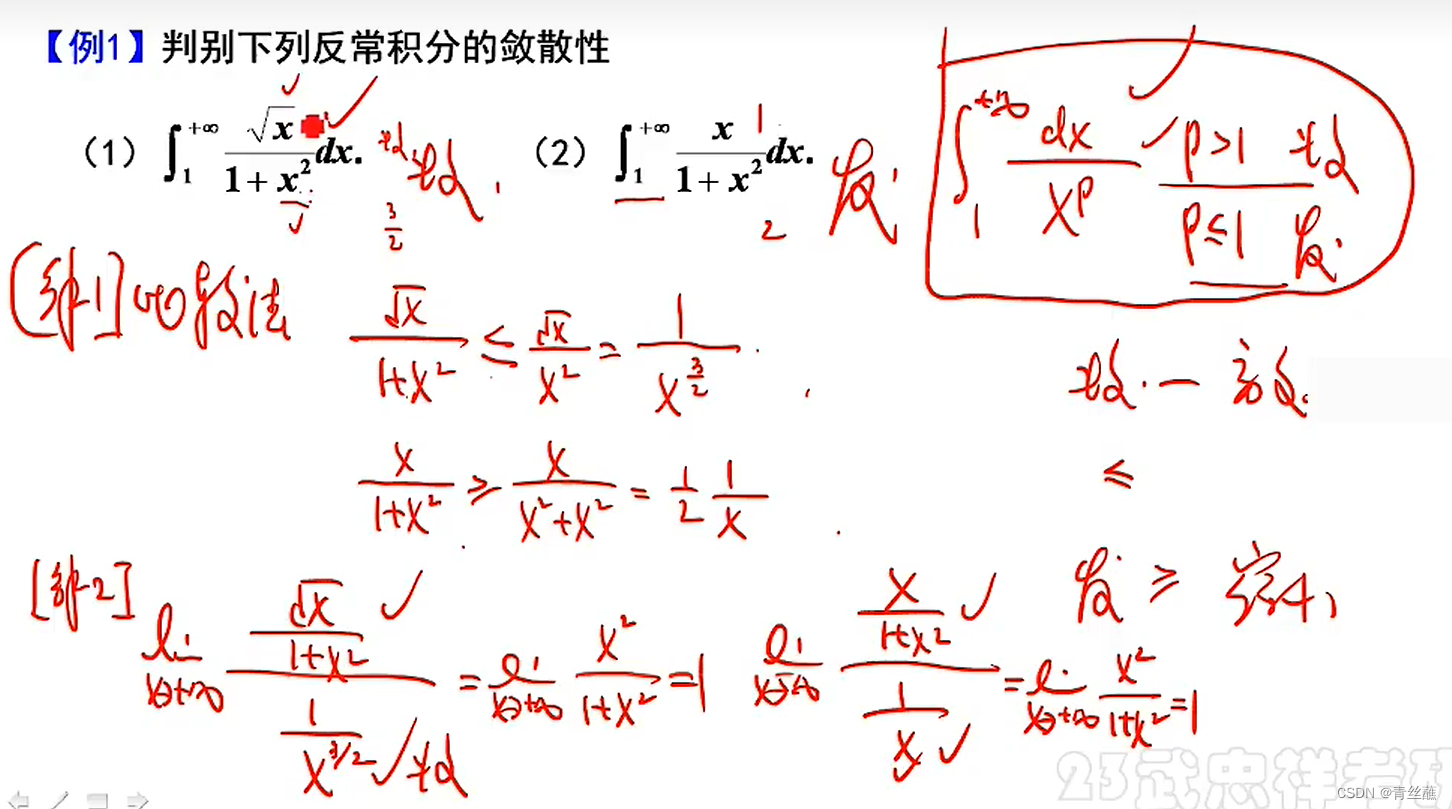
比较对象是我们熟悉的P积分进行比较。
判收敛放大,大的收敛小的就收敛
判发散缩小,小的发散大的就发散
(2)无界函数的反常积分



常考题型与典型例题:
(1)反常积分的敛散性
(1)定义:原函数比较好找的情况下
(2)比较法:和P积分比较
(3)P积分

(2)反常积分的计算
(1)换元(定积分不分第一类换元第二类换元,统称为换元;不定积分才分第一类换元第二类换元 )
(2)分部
ch6 定积分的应用
1.平面图形的面积
(1)直角坐标
(2)极坐标

2.旋转体体积
(1)区域D绕x轴旋转一周所得到的旋转体体积为
Vx=pi∫f²(x)dx
(2)区域D绕y轴旋转一周所得到的旋转体体积为
Vy=2pi∫xf(x)dx

3.曲线弧长
(1)
(2)
(3)

4.旋转体侧面积
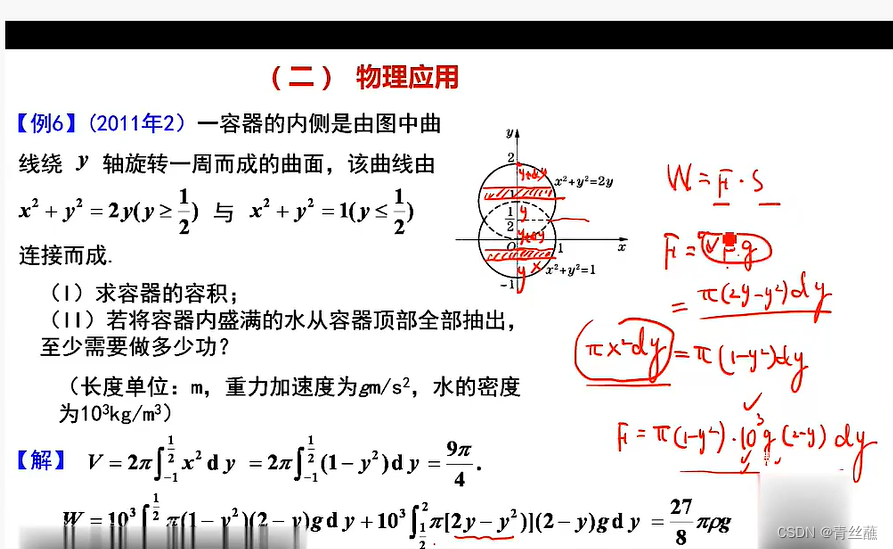
sec2 物理应用
1.压力:
2.变力做功:
3.引力:

ch7 常微分方程
sec1.常微分方程的基本概念
1.微分方程
2.微分方程的阶
3微分方程的解
4.微分方程的通解
5.微分方程的特解
6.微分方程的初始条件
7.积分曲线
sec2.一阶微分方程
(1)可分离变量的方程 y’=f(x)g(y)
(2)齐次方程:dy/dx=&(y/x) 令u=y/x => y=xu. dy/dx=u+x(du/dx)=&(u) 可分
(3)线性方程; y’+P(x)y=Q(x) 通解:略 【注】在代入通解公式算e上面的积分时,e上面的出现1/x的积分不用加绝对值也不用加任意常数。
(4)伯努利方程(仅数一):y’+P(x)y+Q(x)(y^a) (a!=1) 令y^(1-a)=u,将方程化为线性方程。
(5)全微分方程(仅数一): dF(x,y)=P(x,y)dx+Q(x,y)dy=0. a.判定:P对y的偏导等于Q对x的偏导。b.解法:(1)偏积分(2)凑微分(3)线积分
sec3.可降价的高阶方程
y”=f(x,y,y’)
(1)y”=f(x)
(2)y”=f(x,y’)不显含y的微分方程 :令 y’=P,y”=dP/dx
(3)y”=(y,y’)不显含x的微分方程 :令 y’=P,y”=P(dP/dy)
sec4.高阶线性微分方程
(1)线性微分方程的解的结构
齐次方程: y”+p(x)y’+q(x)y=0 (1)
非齐次方程 y”+p(x)y’+q(x)y=f(x) (2)
定理1:如果y1(x)和y2(x)是齐次方程(1)的两个线性无关的特解,那么有y=C1y1(x)+C2y2(x)就是方程(1)的通解。
定理2:如果y*是非齐次方程(2)的一个特解,y1(x)和y2(x)是齐次方程(1)的两个线性无关的特解,则y=C1y1(x)+C2y2(x)+y*(x)是非齐次微分方程(2)的通解。
定理3:如果y1*(x),y2*(x)是非齐次方程(2)的两个特解,则y(x)=y2*(x)-y1*(x)是齐次微分方程(1)的解。
定理4:如果y1*(x),y2*(x)分别是方程y”+p(x)y’+q(x)y=f1(x) ,y”+p(x)y’+q(x)y=f2(x) 的特解,则y1*(x)+y2*(x)是方程y”+p(x)y’+q(x)y=f1(x)+f2(x)的一个特解。
(2)常系数齐次线性微分方程
y”+py’+qy=0
特征方程 r²+pr+q=0;
设r1,r2是特征方程两个根
1)不等实根:r1!=r2 y=C1(e^(r1x)+C2(e^(r2x)
2)相等实根: r1=r2=r y=(e^(rx))*(C1x+C2);
3)共轭复根: r1,2=a±iB y=(e^(ax))*(C1cosBx+C2sinBx)
(3)常系数非齐次线性微分方程

(4)欧拉方程(仅数一)

sec5差分方程(仅数三)
题型一 微分方程求解



题型二 综合题


【注】条件是f(x)连续,为什么能求f’(x)?因为求导后可以看出f’(x)=f(x)+e^x是连续的。所以能用。
题型三 应用题
ch8 多元函数微分学
sec1. 多元函数的基本概念
1.重极限 连续 偏导数 全微分
2.常考题型与典型例题 讨论连续性、可导性、可微性
(1)多元函数的极限
lim[(x,y)->(x0,y0)] f(x,y)=A
【注】
1)(x,y)->(x0,y0)是以“任意方式”
2)(1)局部有界性(2)保号性(3)有理运算(4)极限与无穷小的关系(5)夹逼性
多元函数求极限:存在,方法步骤:(1)取绝对值(2)夹逼
不存在,方法步骤:找反例
(2)多元函数的连续性
(1)连续的概念 lim[(x,y)->(x0,y0)] f(x,y)=f(x0,y0)
(2)连续函数的性质
性质1 多元函数的和差积商(分母不为零)仍为连续函数;
性质2 多元连续函数的复合函数也是连续函数;
性质3 多元初等函数在其定义区域内连续
性质4 (最大值定理) 有界闭区域D上的连续函数在区域D上必能取得最大值与最小值。
性质5 (介值定理)有界闭区域D上的连续函数在区域D上必能取得介于最大值与最小值之间的任何值。
(3)偏导数
1)偏导数的定义
略
2) 二元函数偏导数的几何意义
z=f(x,y)是一个曲面
z=f(x,y0)表示y=y0这个平面与曲面的交线。z=f(x,y)在y=y0的偏导就是这条曲线的导数。
3)高阶偏导数
定义5 略
定理1 如果函数z=f(x,y)的两个二阶混合偏导数f’‘xx和f”yy在区域D内连续,则在该区域内f’‘xx=f”yy。
(4)全微分
定义5 若△z=f(x0+△x,y0+△y)-f(x0,y0)=A△x+B△y+o(p),则称函数z=f(x,y)在点(x0,y0)处可微,dz=A△x+B△y
定理2(可微的必要条件) 如果z=f(x,y)在点(x0,y0)处可微,则在点(x0,y0)处z’x,z’y必定存在,且dz=z’xdx+z’ydy。
用定义判定可微性
a)首先,fx(x0,y0)与fy(x0,y0)是否都存在?
b)然后,lim[] {△z-[fx(x0,y0)△x+fy(x0,y0)△y]}/[(△x)²+(△y)²]½
定理3(可微的充分条件)如果z=f(x,y)的偏导数z’x,z’y在点(x0,y0)处连续,则函数z=f(x,y)在点(x0,y0)处可微。(偏导存在且在该点连续,则函数在该点可微)
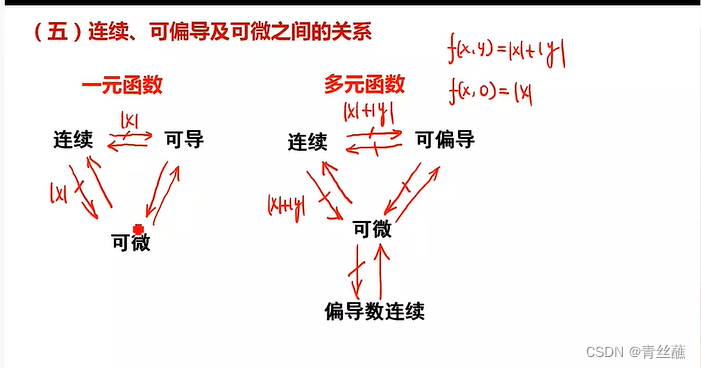
(5)连续、可偏导及可微之间的关系
偏导数连续一定可微,但可微不一定偏导数连续。
2.常考题型与典型例题 讨论连续性、可导性、可微性





sec2. 多元函数微分法
1.复合函数的微分法
定理4 设u=u(x,y),v=v(x,y)在点(x,y)处有对x及对y的偏导数,函数z=f(u,v)在对应点(u,v)处有连续偏导数,则z=f[u(x,y),v(x,y)]在点(x,y)处的两个偏导数存在。且有z’x=z’u·u’x+z’v·v’x,z’x=z’u·u’y+z’v·v’y。
全微分形式的不变性
设函数z=f(u,v),u=u(x,y)及v=v(x,y)都有连续的一阶偏导数,则复合函数z=f[u(x,y),v(x,y)]的全微分dz=z’xdx+z’ydy=z’udu+z’vdv.
2.隐函数的微分法
1)由方程F(x,y)=0确定的隐函数y=y(x)
y’=-(F’x/F’y).
2)由方程F(x,y,z)=0确定的隐函数z=z(x,y)
若F(x,y,z)在点P(x0.y0,z0)的某一邻域内由连续偏导数,且F(x0,y0,z0)=0,F’z(x0,y0,z0)!=0。则方程F(x,y,z)=0在点(x0,y0,z0)的某邻域可唯一确定一个有连续偏导数的函数z=z(x,y),并有z’x=-(F’x/F’z),z’y=-(F’y/F’z).
常考题型
题型一 复合函数的偏导数与全微分
先代后求

题型二 隐函数的偏导数与全微分
(1)对等式两端求偏导
(2)公式法
(3)微分形式的不变性

sec3.多元函数的极值与最值
1.无约束极值
定义7:若在点(x0,y0)的某邻域内恒成立不等式f(x,y)<=f(x0,y0) ( f(x,y)>=f(x0,y0) )
则称f在点(x0,y0)取得极大值(极小值)。点(x0,y0)称为f的极大值点(极小值点),极大值点与极小值点统称为极值,极大值点与极小值点统称为极值点。
定理5(极值的必要条件):设z=f(x,y)在点(x0,y0)存在偏导数,且(x0,y0)为f(x0,y0)的极值点,则f’x(x0,y0)=0,f’y(x0,y0)=0.
驻点不一定是极值点;反例xy
极值点不一定是驻点;反例|x|+|y|
可导情况下极值点是驻点。
可能极值点:(1)驻点(2)偏导数不存在的点
定理6(极值的充分条件)设z=f(x,y)在点P0(x0,y0)的某邻域内有二阶连续偏导数,又f’x(x0,y0)=f’y(x0,y0)=0,记A=f”xx(x0,y0),B=f”xy(x0,y0),C=f”yy(x0,y0),则
(1)当AC-B²>0时,有极值;A>0极小值,A<0极大值
(2)当AC-B²<0时,无极值。
(3)当AC-B²=0时,不一定(一般用定义判定)。
2.条件极值与拉格朗日乘数法
1)函数f(x,y)在条件Φ(x,y)=0条件下的极值。
令F(x,y,入)=f(x,y)+入Φ(x,y)
F’x=f’x(x,y)+入Φ’x(x,y)=0,
F’y=f’y(x,y)+入Φ’y(x,y)=0,
F’入=Φ(x,y)=0,
2)函数f(x,y,z)在条件Φ(x,y)=0,Ψ(x,y,z)=0条件下的条件极值
令F(x,y,z.入.u)=f(x,y,z)+入Φ(x,y,z)+uΨ(x,y,z)
3.最大最小值
1.求连续函数f(x,y)在有界闭区域D上的最大最小值
1)求f(x,y)在D内部可能的极值点。
2)求f(x,y)在D的边界上的最大最小值。
3)比较
2.应用题
常考题型
题型一 求极值(无条件)


题型二求连续函数f(x,y)在有界闭区域D上的最大最小值

题型三最大最小值应用题
处理边界:(1)拉格朗日常数法(2)直角坐标下,化条件为无条件(3)遇到圆椭圆等曲线边界,在参数方程下化条件为无条件



ch9: 二重积分
1.二重积分的概念与性质
(1)二重积分的概念:
定义1:∫∫【D】f(x,y)dσ=lim【入->0】 Σ【i=1,n】f(xi,yi)Δσi.
几何意义:略
(2)二重积分的性质
性质1(不等式)
(1)在D上若f(x,y)≤g(x,y),则∫∫【D】f(x,y)dσ<=∫∫【D】g(x,y)dσ,
(2)若在D上有m<=f(x,y)<=M,则mS<=∫∫【D】f(x,y)dσ<=MS,其中S为区域D的面积。
性质2(中值定理)设函数f(x,y)在闭区域D上连续,S为区域D的面积,则在D上至少存在一点(ξ,η),使得∫∫【D】f(x,y)dσ=f(ξ,η)·S
2.二重积分计算
(1)利用直角坐标计算
1)先y后x ∫∫【D】f(x,y)dσ=∫【a,b】dx∫【φ1(x),φ2(x)】f(x,y)dy
2)先x后y ∫∫【D】f(x,y)dσ=∫【c,d】dy∫【φ1(y),φ2(y)】f(x,y)dx
(2)利用极坐标计算
1)先р后θ ∫∫【D】f(x,y)dσ=∫【α,β】dy∫【φ1(θ),φ2(θ)】f(рcosθ,рsinθ)рdр
【注】适合用极坐标计算的二重积分的特征
(1)适合用极坐标计算的被积函数:
f( (x²+y²)^(1/2) ) ,f(y/x),f(x/y)
(2)适合极坐标的积分域:如
x²+y²≤R²; r²≤x²+y²≤R²;
x²+y²≤2ax; x²+y²≤2by;
圆心既不在坐标原点也不在坐标轴上的积分域,令x-x0=pcosθ,y-y0=psinθ; 【???】
(3)利用对称性和奇偶性计算
1)若积分域D关于y轴对称,则
当f(-x,y)=f(x,y)时, ∫∫【D】f(x,y)dσ=2∫∫【D1】f(x,y)dσ;
当f(-x,y)=-f(x,y)时, ∫∫【D】f(x,y)dσ=0;
2)若积分域D关于x轴对称,则
当f(x,-y)=f(x,y)时, ∫∫【D】f(x,y)dσ=2∫∫【D1】f(x,y)dσ;
当f(x,-y)=-f(x,y)时, ∫∫【D】f(x,y)dσ=0;
(4)利用变量对称性计算
若D关于y=x对称,则∫∫【D】f(x,y)dσ=∫∫【D】f(y,x)dσ
常考题型
题型一:累次积分交换次序及计算

题型二:二重积分计算


(凑数的题)
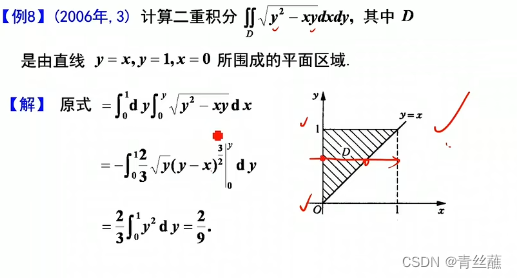




题型三:不等式


ch10:无穷级数
sec1:常数项级数(数一数二要求)
(1)概念与性质
(1)级数的概念
Σ【n=1,∞】un=u1+u2+……+un+……
sn=Σ【i=1,n】ui(部分和)
Σ【n=1,∞】un=lim【n->∞】sn
研究两个问题:级数收敛还是发散,级数的和
(2)级数的性质
(1)若Σ【n=1,∞】un收敛于s,则Σ【n=1,∞】kun也收敛,且其和为ks.
(2)若Σ【n=1,∞】un和Σ【n=1,∞】vn,分别收敛于s,σ.则Σ【n=1,∞】(un±vn)收敛于s±σ。
【注】收敛±发散=发散;发散±发散=不确定。
(3)在级数中去掉、加上或改变有限项不影响级数的敛散性。
(4)收敛级数加括号仍收敛且和不变。
【注】加括号收敛 不能得 原级数收敛;原级数收敛 可以得加括号收敛。
加括号发散 可以得 原级数发散。
(5)级数收敛得必要条件
Σ【n=1,∞】un收敛 ——>lim【n->∞】un=0.
lim【n->∞】un=0 不能得Σ【n=1,∞】un收敛。 经典反例:Sn=Σ【n=1,∞】(1/n).
(2)级数的审敛准则
(1)正项级数 (Σ【n=1,∞】un,un≥0)
基本定理:Σ【n=1,∞】un收敛 《=》sn上有界
1)比较判别法法:设un≤vn,则
Σ【n=1,∞】vn收敛 =>Σ【n=1,∞】un收敛
Σ【n=1,∞】un发散 =>Σ【n=1,∞】vn发散
补充:Σ【n=1,∞】un发散 =>Sn->+∞。
2)比较法的极限形式:设lim【n->∞】(un/vn)=l (0<=l<=+∞)
a.若0<l<+∞,则Σ【n=1,∞】un与Σ【n=1,∞】vn同敛散。
b.若l=0,则Σ【n=1,∞】vn收敛=>Σ【n=1,∞】un收敛,Σ【n=1,∞】un发散 =>Σ【n=1,∞】vn发散;
c.若l=+∞,则Σ【n=1,∞】vn发散=>Σ【n=1,∞】un发散,Σ【n=1,∞】un收敛=>Σ【n=1,∞】vn收敛.
两个常用级数:
1)Σ【n=1,∞】1/(n^p) p>1时收敛,当p<=1时发散;
2)Σ【n=1,∞】a(q^n) (a>0,q>0) q<1时收敛,当q>=1时发散。
3)比值法:设lim【n->∞】(un+1/un)=ρ,则
当ρ<1时,Σ【n=1,∞】un收敛; 当ρ>1时,Σ【n=1,∞】un发散; 当ρ=1时,Σ【n=1,∞】un不一定。
4)根值法:设lim【n->∞】(un)^(1/n)=ρ,则
当ρ<1时,Σ【n=1,∞】un收敛; 当ρ>1时,Σ【n=1,∞】un发散; 当ρ=1时,Σ【n=1,∞】un不一定。
5)积分判别法:设f(x)是【1,+∞)上单调减,非负的连续函数,且an=f(n)则Σ【n=1,∞】an与∫【1,+∞】f(x)dx同敛散。
总结:1)、2):适用范围广但不方便。
3)、4):方便但适用范围窄。
【注】出现a^n,n!,n^n其中之一,用3)4);否则用1)2)。
(2)交错级数 (Σ【n=1,∞】[(-1)^n]un,un>0)
莱布尼茨准则:(1)若(1)un单调减;(2)lim【n->∞】un=0;则Σ【n=1,∞】[(-1)^(n-1) ]un收敛。
【注】Σ【n=1,∞】[(-1)^(n-1) ]un收敛 推不出 un单调减且lim【n->∞】un=0;
un单调减且lim【n->∞】un=0 可以推出 Σ【n=1,∞】[(-1)^(n-1) ]un收敛 。
(3)任意项级数
1)绝对收敛与条件收敛的概念
(1)若Σ【n=1,∞】|an|收敛,则Σ【n=1,∞】an必收敛,此时称Σ【n=1,∞】an绝对收敛。
(2)如Σ【n=1,∞】an收敛,Σ【n=1,∞】|an|发散,则称Σ【n=1,∞】an条件收敛。
2)绝对收敛和条件收敛的基本结论
(1)绝对收敛的级数一定收敛,即Σ【n=1,∞】|un|收敛 => Σ【n=1,∞】un收敛。
(2)条件收敛的级数的所有正项(或负项)构成的级数一定发散。即:
Σ【n=1,∞】un条件收敛 =>Σ【n=1,∞】[un-|un|]/2发散。
常考题型:
- 常数项级数敛散性判定




sec2:幂级数(数一数三要求)
sec3:傅里叶级数(仅数一要求)
