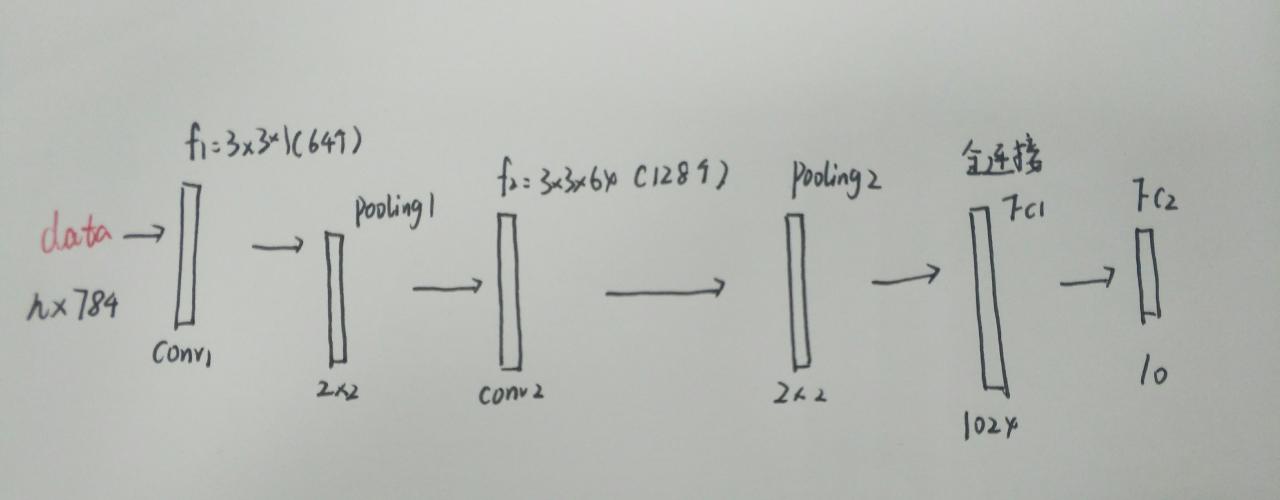
简单的介绍一下构造的的这个比较简单的神经网络的结构,首先,我们这个输入依然是n个样本然后一张图片是784个像素点。第一层我们希望输出是64个特征图,所以我们设定有64个3*3大小的滤波器(卷积核)要注意我们这里的卷积核的深度为1,依赖于灰度图,所以我们输入图像的深度也为1,所以我们要保证卷积核和输入的深度是一致的。然后来到了第一个卷积层之后的池化层,我们设定池化的大小为2*2也就是经历一个池化层之后,图像块的长和宽都缩小一半,所以可以得出经过第一个池化层之后的图像块大小从28*28变到了14*14.
然后我们得到了64个特征图,我们认为此时的深度为64,所以第二层的滤波器(卷积核)的深度也应该为64,所以第二层的卷积核应该是3*3*64,数量是128个,然后在经过一个2*2的池化层既可以得到128个7*7大小的特征图了。然后是全连接层,一般都选取两个全连接层,第一个全连接层我们设置他的神经元的个数是1024个,然后第二个全连接层的神经元个数就是10(我们最终的要分出的类别),对于第一层全连接层来说,我们相当于要把7*7*128的特征图转化成一个1024的列向量。
基本结构就是这些,然后来看看基本的代码。
最基本的还是千篇一律的导入基本库环节;
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import input_data
mnist = input_data.read_data_sets('/home/weiying2/simple cnn/data', one_hot=True)
trainimg = mnist.train.images
trainlabel = mnist.train.labels
testimg = mnist.test.images
testlabel = mnist.test.labels接下来是定义参数的过程:
n_input = 784
n_output = 10
weights = {
'wc1': tf.Variable(tf.random_normal([3, 3, 1, 64], stddev=0.1)),
'wc2': tf.Variable(tf.random_normal([3, 3, 64, 128], stddev=0.1)),
'wd1': tf.Variable(tf.random_normal([7*7*128, 1024], stddev=0.1)),
'wd2': tf.Variable(tf.random_normal([1024, n_output], stddev=0.1))
}
biases = {
'bc1': tf.Variable(tf.random_normal([64], stddev=0.1)),
'bc2': tf.Variable(tf.random_normal([128], stddev=0.1)),
'bd1': tf.Variable(tf.random_normal([1024], stddev=0.1)),
'bd2': tf.Variable(tf.random_normal([n_output], stddev=0.1))
}首先random——normal是高斯初始化然后对于卷积层来说卷积核就是权重参数。他的第一个参数可以看作是一个四维的向量,前两个参数代表了卷积核的大小,第三个参数表示卷积核的深度(深度和输入的深度一致),第四个参数表示卷积核的数量。
stddev是高斯分布的标准差,我们设定这个值为0.01
第二个卷积层的卷积核大小依然是3*3大小然后我们经过第一层的卷积之后我们得到了64个特征图,所以我们认为此时的深度为64,所以第二层卷积层的卷积核的深度就不再为1而是64了。设置第二层的输出为128所以卷积核的个数就是128
对于第一层全连接层来说,设定他的神经元个数为1024,那么前面那一层的输出的神经元个数就需要·通过计算得到,通过第一个池化层之后得到的是14*14*64,经过第二个卷积池化之后得到的是7*7*128。所以神经元个数就是7*7*128。
再来看看这个偏移值就是深度多大就有多少个偏移值,然后也就是神经元的个数决定了你有几个bias值。
def conv_basic(_input, _w, _b, _keepratio):
# INPUT
_input_r = tf.reshape(_input, shape=[-1, 28, 28, 1])#要重新定义输入的格式,因为之后用到的conv2d函数需要这种四维格式的输入。
# CONV LAYER 1
_conv1 = tf.nn.conv2d(_input_r, _w['wc1'], strides=[1, 1, 1, 1], padding='SAME')
#输入为reshape之后的,输入第一层的卷积核参数权重,strides是步长通过这个参数知道每一个参数都应该是四维的。跟别对应图像之间的,h,w,深度之间的步长。
#padding这个参数一共可能取值有两种,一种是same,一种是valid,same的意思是当滑动取图像块时候边界不够了就自动补0,另一种是把边界不够的剩下的直接删除。
#_mean, _var = tf.nn.moments(_conv1, [0, 1, 2])#这个一般是作为batch_normalization的输入
#_conv1 = tf.nn.batch_normalization(_conv1, _mean, _var, 0, 1, 0.0001)
_conv1 = tf.nn.relu(tf.nn.bias_add(_conv1, _b['bc1']))#更新_conv1:加上偏移值同时将此结果进行relu激活函数
_pool1 = tf.nn.max_pool(_conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
#第一个池化层,采取长和宽都缩小一半的方式。这样那个的话你滑动的时候相应的步长也应该为2,2
_pool_dr1 = tf.nn.dropout(_pool1, _keepratio)#dropout:当训练的时候不让所有的神经网络训练而是随即杀死一些神经元。
# CONV LAYER 2
_conv2 = tf.nn.conv2d(_pool_dr1, _w['wc2'], strides=[1, 1, 1, 1], padding='SAME')
#_mean, _var = tf.nn.moments(_conv2, [0, 1, 2])
#_conv2 = tf.nn.batch_normalization(_conv2, _mean, _var, 0, 1, 0.0001)
_conv2 = tf.nn.relu(tf.nn.bias_add(_conv2, _b['bc2']))
_pool2 = tf.nn.max_pool(_conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
_pool_dr2 = tf.nn.dropout(_pool2, _keepratio)
# VECTORIZE
_dense1 = tf.reshape(_pool_dr2, [-1, _w['wd1'].get_shape().as_list()[0]])
#到了全连接层的时候,我们计算神经元的输出就需要使用矩阵乘法了,但是我们全连接层的参数定义的时候和卷积的那个参数纬度是不同的,也就是说明
#我们卷积的输出结果和全连接明显纬度不同,所以为了能够联系起来所以就需要使得我们的网输出的格式和全连接层的参数一样。所以采用了上面的函数最后改成一个列表形式的
# FULLY CONNECTED LAYER 1
_fc1 = tf.nn.relu(tf.add(tf.matmul(_dense1, _w['wd1']), _b['bd1']))#全连接的结果也需要使用relu函数
_fc_dr1 = tf.nn.dropout(_fc1, _keepratio)
# FULLY CONNECTED LAYER 2
_out = tf.add(tf.matmul(_fc_dr1, _w['wd2']), _b['bd2'])#最后一层输出不需要relu函数
# RETURN
out = { 'input_r': _input_r, 'conv1': _conv1, 'pool1': _pool1, 'pool1_dr1': _pool_dr1,
'conv2': _conv2, 'pool2': _pool2, 'pool_dr2': _pool_dr2, 'dense1': _dense1,
'fc1': _fc1, 'fc_dr1': _fc_dr1, 'out': _out
}#每一层的输出还有dropout的结果都需要作为返回值
return out
print ("CNN READY")那么重点就是我们要定义卷积运算并前后向传播的函数了首先这个函数有四个参数_input, _w, _b, _keepratio
前三个分别是输入,权重和偏移值,第四个参数是和神经网络的dropout有关,它是一个比例,为了节省运算时间,神经元每次在进行训练的时候,总会按照一定比例随机锁定一些神经元的权重和偏移值,这个比列就是_keepratio。
然后因为我们之后需要用到conv2d进行卷积操作,所以我们的输入要严格按照conv2d函数每一个参数的格式,它每个参数的格式是四维的,所以需要把输入也变为四维的。首先看下reshape之后的后面三个参数。28,28就是输入图像块的大小,1灰度图的深度,前面的-1是指这第一个参数系统会自动的计算(因为已经知道了后面的三个参数,所以这第一个参数就是用reshape之前的和去除以28*28*1,也就是样本个数n)
x = tf.placeholder(tf.float32, [None, n_input])
y = tf.placeholder(tf.float32, [None, n_output])
keepratio = tf.placeholder(tf.float32)#
# FUNCTIONS
_pred = conv_basic(x, weights, biases, keepratio)['out']#因为返回值太多所以指定pred值就是返回的“out”
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(_pred, y))#代价函数用softmax的交叉熵函数替代
optm = tf.train.AdamOptimizer(learning_rate=0.001).minimize(cost)#用Adam优化算法来代替梯度下降算法,优点是不容易陷入局部最优点,速度更快因为adam算法引入了二次梯度校正
#计算精度
_corr = tf.equal(tf.argmax(_pred,1), tf.argmax(y,1))
accr = tf.reduce_mean(tf.cast(_corr, tf.float32))
init = tf.global_variables_initializer()#全局变量初始化
# SAVER
print ("GRAPH READY")
sess = tf.Session()
sess.run(init)
training_epochs = 100
batch_size = 100
display_step = 1
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples/batch_size)
# total_batch = 10
# Loop over all batches
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# Fit training using batch data
sess.run(optm, feed_dict={x: batch_xs, y: batch_ys, keepratio:0.7})
# Compute average loss
avg_cost += sess.run(cost, feed_dict={x: batch_xs, y: batch_ys, keepratio:1.})/total_batch
# Display logs per epoch step
if epoch % display_step == 0:
print ("Epoch: %03d/%03d cost: %.9f" % (epoch, training_epochs, avg_cost))
train_acc = sess.run(accr, feed_dict={x: batch_xs, y: batch_ys, keepratio:1.})
print (" Training accuracy: %.3f" % (train_acc))
#test_acc = sess.run(accr, feed_dict={x: testimg, y: testlabel, keepratio:1.})
#print (" Test accuracy: %.3f" % (test_acc))
print ("OPTIMIZATION FINISHED")然后这样迭代一次(cpu)i3处理器,8g内存,15min就没做下去,精度竟然到达了0.99.看来这个数据集还是比较简单但是如果每次不把训练样本取完就是total——batch取10就会很差结果。。。。