1 矩阵的几个概念
1.1 特殊矩阵
1.1.1 数量矩阵
主对角线上元素是同一个数,其余元素全为0的n级矩阵
1.1.2 对角矩阵(diagonal matrix)
主对角线元素之外全为0的方阵
记作diag{d1,d2,……dn}
1.1.3 基本矩阵
只有一个元素是1,其余元素全为0的矩阵
(i,j)元为1的基本矩阵:Eij
用Eij左乘(右乘)一个矩阵A,就相当于把A的第j行搬到第i行(第i列搬到第j列),而其余元素变为0 【左行右列】
1.1.4
初等矩阵
由单位矩阵经过一次初等行/列变换得到的矩阵
用初等矩阵左乘(右乘)一个矩阵,相当于对这个矩阵做相应的初等行(列)变换【左行右列】
1.1.5 单位矩阵

1.2 可交换
如果AB=BA,那么A,B可交换
一般来说,
≠
,但是如果A,B可交换,那么
=
1.3 矩阵集合

2 初等行变化与矩阵相乘

3 阶梯矩阵REF和简化阶梯矩阵RREF
3.1 REF
Row Echelon Form 行阶梯矩阵

3.2 RREF
Reduced Row Echelon Form 简化行阶梯矩阵


3.3 RREF 和原始矩阵之间的关系
初等行变换不改变列之间的线性关系


span——向量张成的空间
因为初等行变换之后,行相当于是等价的,原来能线性表出哪些向量,现在还能;而列就不一样了。
4 矩阵向量乘法
矩阵相当于一个线性系统
对于一个多元线性方程组如下图,输入为
x
=[
x
1
x
2
x
3
…
xn
]
,经过一个线性变换后,输出为
b
=[
b
1
b
2
x
3
…
bm
]
,这个线性系统便是对
x
做了一个线性的处理,其处理的方法为矩阵
A
‘
对一个系数矩阵
A
m
×
n
和一个代表参数的向量
x
n
相乘,拿下图举例,有两种理解方式:

从行层面上理解:
将
A
的两行表示在坐标系中如下图右侧所示;对照方程组,将向量中的
x
1
x
2
与矩阵行中的元素对应相乘后组成向量:首先是
A
1
,:
与
x
相乘,发现结果为
0
,证明二者垂直,而后是
A
2
,:
与
x
相乘,得出结果。
(每一个维度是A的一行与x的内积)
——>结果的每一个维度都是A对应的行和x的内积结果

从列层面上理解:
数据域的
x
1
与
A
:,1
相乘,相当于逆向延长两倍
[1 −3]
这个向量,同理,
x
2
与
A
:,2
相乘,相当于正向缩小为原来长度的一半,二者形成的列向量叠加后与
1有相同的结果。——>
结果是以x为系数,A每一列为向量的矢量和

5 矩阵乘法
矩阵的乘法相当于两个线性函数的组合


5.1 矩阵相乘的先后顺序对于运算速度的影响
虽然使用交换律对矩阵相乘的结果没有什么影响,但是对于运算的次数,先进行分析,再视情况适当交换运算顺序会带来很大的效益
(三个矩阵相乘的规则是按顺序两两相乘,因此运算次数是加的关系,不同结合情况对运算次数显然有不同影响)。

矩阵 A(M*N) 和矩阵B(N*P)相乘,A的每一行要和B的每一列进行内积(也就是进行N次乘法+N次求和),
—>然后A和B分别由M行和P列,相当于一共M*P对行列对
—>所以这两个矩阵相乘,相当于M*N*P次操作
回到这个问题,如果是先CP,再A和乘积相乘,那么CP需要M*N*P次操作,10^6数量级;然后A在和结果相乘K*M*P,又是10^6数量级
如果是先AC,那么是K*M*N,1000的数量级;然后结果再和P相乘K*N*P ,1000的数量级
5.2 GPU的加速效果

6 可逆矩阵
6.1
互为可逆矩阵

6.2 可逆矩阵唯一
如果AB=I,AC=I,那么B=C
证明:
B=B(AC)=(BA)C=C
6.3 矩阵乘积的逆
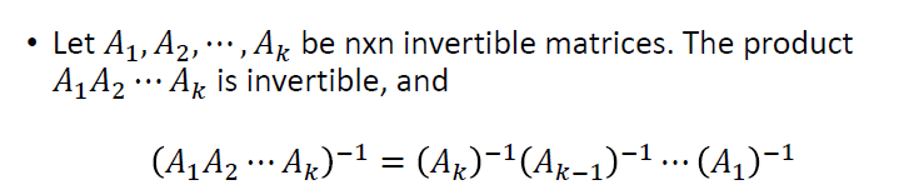
6.4 矩阵转置的逆
![]()
6.5 矩阵可逆的条件

说白了就是方阵满秩
换言之,
如果一个矩阵A是可逆的,当且仅当A的简化阶梯矩阵是单位矩阵

6.6 为何可逆矩阵需要满秩方阵?
6.6.1
单射(one to one)
单射:每个v射向不同的f(v),但不一定每个f(v)都会被射到

如果是矮胖型的矩阵,那么列之间肯定线性相关,那么对于某一个特定的 f(v) ,会存在两个不同的v1和v2,使得f(v1)=f(v),f(v2)=f(v),不满足单射(每个v射向不同的f(v)的条件
而单射的逆呢?因为不一定每个f都被映射到,所以单射的逆不能保证也是单射(可能会由在域空间上的值不在定义域空间内)
为了保证one to one ,也就是每个v,f(v)的值不同,我们需要矩阵A各个列线性无关
6.6.2 满射(onto)

满射是值每个值域空间的点都会被映射到(虽然可能多个v射到一个值域上去)
也就是说,对于任意一个b,Av=b都有解,
按照前面的说法(“线性方程有解的充要条件”),矩阵A的简化阶梯矩阵不能有0行(也就是说,它不能是高瘦型矩阵);同时它的秩等于它的行数
满射的逆甚至可能不是映射(一个值域上的值可能对应了几个定义域上的值)
6.6.3 矩阵可逆的条件
所以如果一个矩阵可逆,那么它必须同时是单射和满射

‘

6.7 矩阵逆的求法



6.8 用伴随矩阵求矩阵的逆

伴随矩阵
C的每个元素是A对应的代数余子式

证明

矩阵的行列式=某一行元素*其代数余子式的和
Σ第i行元素*第j行元素的代数余子式=0


