文章目录
1. 质数
在 > 1的整数中, 如果只包含1和本身这两个约数,就是质数,也叫素数
n <= 1不是质数
质数的判定-试除法
质数的约数都是成对出现的,可以枚举每一对中较小的那个
// O(sqrt(n))
bool is_prime(int n){
if(n <= 1) return false;
for(int i = 2; i <= n / i; i++) // i * i <= n 可能会越界
if(n % i == 0)
return false;
return true;
}
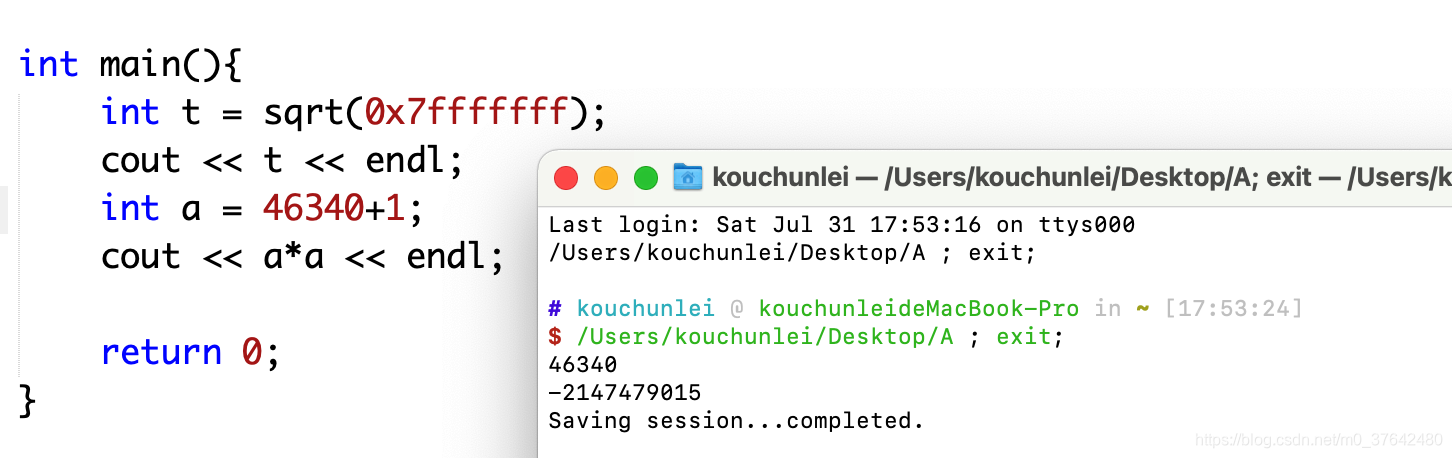
为什么是 i <= n/i
稍微好一点,临界情况 i*i会爆掉
分解质因数-试除法
O(n)
//分解质因数
void divide(int n){
for(int i = 2; i <= n; i++){
if(n % i == 0){ // [2~i-1]的因子都除干净了, i 一定是质数
int s = 0;
while(n % i == 0){
s++;
n /= i;
}
cout << i << " " << s << endl;
}
}
cout << endl;
}
// O(sqrt(n))
//只有一个 > sqrt(n) 的质因子
void divide(int n){
for(int i = 2; i <= n/i; i++){
if(n % i == 0){
int s = 0;
while(n % i == 0){
s++;
n /= i;
}
cout << i << " " << s << endl;
}
}
if(n > 1) cout << n << " 1" << endl; // > sqrt(n)的质因子
cout << endl;
}
AcWing 868. 筛质数
朴素做法
int prime[N],cnt; /prime存放质数的值,cnt计数,下标
bool st[N];
/O(nlog(n))
void get_prime(int n){
for(int i = 2; i <= n; i++){
if(!st[i]) prime[cnt++] = i;
for(int j = i; j <= n; j = j + i) st[j] = true;
}
}

如果 2~p-1中,枚举的不是质数,那么该数不可能是 p 的约数!!
1~n中有 n/ln(n) 个质数 = nlogn个数,少算logn倍
所以比朴素筛法快了 log(n)倍
埃式筛法
/ O(nlog(log(n)) = O(n)
void get_prime(int n){
for(int i = 2; i <= n; i++){
if(!st[i]){
prime[cnt++] = i;
/优化,只删除质数的倍数
for(int j = i; j <= n; j = j + i) st[j] = true;
}
}
}
线性筛法
线性筛法,在 n = 1e6 和 埃式筛法差不多
在 n = 1e7的时候,比埃式筛法快一倍
// O(n)
void get_prime(int n){
for(int i = 2; i <= n; i++){
if(!st[i]) primes[cnt++] = i;
for(int j = 0; primes[j] <= n / i; j ++){
// primes[j] 筛掉 primes[j]*i = x
st[primes[j]*i] = true;
if(i % primes[j] == 0) break; // primes[j] 是 i 的最小质因子
}
}
}
假设
i 是合数 t 的最大因数
,t 显然可能不唯一(例如 30 和 45 最大因数都是 15。但是仔细想一想,必然有
t = i * p
(
p为小于 i 的质数
) (i是t的最大因数)
p为什么比 i 小
因为 i 是 t 的最大因数。
为什么 p 一定是质数?
因为如果 p 是合数,那么 i 就一定不是 t 的最大因数,因为 p可以再拆成若干素数相乘,这些素数再与 i 相乘会使因数更大。
既然如此,我们只需要把所有小于 i 的质数 p 都挨个乘一次好了。可是,真相真的是这样的嘛?
其实不是的,一不小心就忘记了最初的条件。我们要满足 i 是 t 的最大因数。如果 p 大于 i 的最小质因数,那 i 还是 t 的最大因数嘛?显然不是,任何一个合数都能唯一分解为有限个质数的乘积,除去这其中最小的质因数,其他的都乘起来就是最大因数 i 。所以我们不能让 p 大于 i 的最小质因数。
n只会被最小质因子筛掉
st[primes[j]*i] = true;
i % pj == 0 , pj 一定是i的最小质因子(primes[]数组存放的是所有的质数),pj 一定是 pj*i 的最小质因子
i% pj != 0 , pj一定小于i的所有质因子, pj 也一定是 pj*i的最小质因子
如何保证所有的合数都被删掉?
任何一个数都存在最小质因子
对于一个合数x,假设pj是x的最小质因子,当i 枚举到 x/pj的时候,x被筛掉
i 枚举到x之前肯定会被筛掉
void get_prime(int n){ // 线性筛法
for(int i = 2; i <= n; i++){
if(!st[i]) primes[cnt++] = i;
//保证primes[j] 是 primes[j]*i 的最小质因数
// 并且 x = primes[j]*i 是 被最小质因数筛掉的
// 并且每个合数x都有最小质因数,都会被筛掉
for(int j = 0; primes[j] <= n/i; j++){
st[primes[j]*i] = true;
if(i % primes[j] == 0) break;
}
}
}
2. 约数
1. 试除法求约数
int a; cin >> a;
vector<int> vec;
for(int i = 1; i <= a/i; i++){
if(a % i == 0){
vec.push_back(i);
if(i != a/i) vec.push_back(a/i); // 16 = 4*4,只放一次4
}
}
AcWing 870. 约数个数
N
=
p
1
α
1
∗
p
2
α
2
∗
p
3
α
3
∗
.
.
.
∗
p
k
α
k
N=p_1^{\alpha_1}*p_2^{\alpha_2} *p_3^{\alpha_3}*…*p_k^{\alpha_k}
N
=
p
1
α
1
∗
p
2
α
2
∗
p
3
α
3
∗
.
.
.
∗
p
k
α
k
a
n
s
=
(
α
1
+
1
)
(
α
2
+
1
)
.
.
.
(
α
k
+
1
)
ans=(\alpha_1+1)(\alpha_2+1)…(\alpha_k+1)
a
n
s
=
(
α
1
+
1
)
(
α
2
+
1
)
.
.
.
(
α
k
+
1
)
因为N的任何一个约数d可以表示成
d
=
p
1
β
1
∗
p
2
β
2
∗
.
.
.
p
k
β
k
,
(
0
<
=
β
i
<
=
α
i
)
d=p_1^{\beta_1}*p_2^{\beta_2}*…p_k^{\beta_k}, (0<=\beta_i<=\alpha_i)
d
=
p
1
β
1
∗
p
2
β
2
∗
.
.
.
p
k
β
k
,
(
0
<
=
β
i
<
=
α
i
)
每一项的
β
i
\beta_i
β
i
如果不同,那么约数d就不同
n的约数个数是与
β
i
\beta_i
β
i
的选法是一一对应的
β
1
一
共
有
0
−
α
1
中
选
法
\beta_1一共有0-\alpha_1中选法
β
1
一
共
有
0
−
α
1
中
选
法
β
2
一
共
有
0
−
α
2
中
选
法
\beta_2一共有0-\alpha_2中选法
β
2
一
共
有
0
−
α
2
中
选
法
…
β
k
一
共
有
0
−
α
k
中
选
法
\beta_k一共有0-\alpha_k中选法
β
k
一
共
有
0
−
α
k
中
选
法
d 有
(
α
1
+
1
)
∗
(
α
2
+
1
)
∗
.
.
.
∗
(
α
k
+
1
)
(\alpha_1+1)*(\alpha_2+1)*…*(\alpha_k+1)
(
α
1
+
1
)
∗
(
α
2
+
1
)
∗
.
.
.
∗
(
α
k
+
1
)
中选法
选法原理
#include <iostream>
#include <unordered_map>
using namespace std;
unordered_map<int,int> mp;
const int MOD = 1e9 + 7;
int main(){
ios::sync_with_stdio(false); cin.tie(0);
int T; cin >> T; while(T--){
int n; cin >> n;
for(int i = 2; i <= n/i; i++){ //寻找质因数,只有一个 > sqrt(n)的质因子
while(n % i == 0){
mp[i]++;
n /= i;
}
}
if(n > 1) mp[n]++;
}
long long ans = 1;
for(auto p : mp){
ans = ans * (p.second + 1) % MOD;
}
cout << ans << endl;
return 0;
}
AcWing871. 约数之和
N
=
p
1
α
1
∗
p
2
α
2
∗
p
3
α
3
∗
.
.
.
∗
p
k
α
k
N=p_1^{\alpha_1}*p_2^{\alpha_2} *p_3^{\alpha_3}*…*p_k^{\alpha_k}
N
=
p
1
α
1
∗
p
2
α
2
∗
p
3
α
3
∗
.
.
.
∗
p
k
α
k
a
n
s
=
(
p
1
0
+
p
1
1
+
.
.
.
+
p
1
α
1
)
∗
.
.
.
∗
(
p
k
0
+
p
k
1
+
.
.
.
+
p
k
α
k
)
ans=(p_1^0+p_1^1+…+p_1^{\alpha_1})*…*(p_k^0+p_k^1+…+p_k^{\alpha_k})
a
n
s
=
(
p
1
0
+
p
1
1
+
.
.
.
+
p
1
α
1
)
∗
.
.
.
∗
(
p
k
0
+
p
k
1
+
.
.
.
+
p
k
α
k
)
将ans展开后,每一项都是一个约数 d
a
n
s
=
d
1
∗
d
2
∗
.
.
.
∗
d
k
ans=d_1*d_2*…*d_k
a
n
s
=
d
1
∗
d
2
∗
.
.
.
∗
d
k
d
i
=
p
1
β
1
∗
p
2
β
2
∗
.
.
.
p
k
β
k
,
(
0
<
=
β
i
<
=
α
i
)
d_i=p_1^{\beta_1}*p_2^{\beta_2}*…p_k^{\beta_k}, (0<=\beta_i<=\alpha_i)
d
i
=
p
1
β
1
∗
p
2
β
2
∗
.
.
.
p
k
β
k
,
(
0
<
=
β
i
<
=
α
i
)
#include <iostream>
#include <unordered_map>
using namespace std;
unordered_map<int,int> mp;
const int MOD = 1e9 + 7;
int main(){
ios::sync_with_stdio(false); cin.tie(0);
int T; cin >> T; while(T--){
int n; cin >> n;
for(int i = 2; i <= n/i; i++){ //寻找质因数,只有一个 > sqrt(n)的质因子
while(n % i == 0){
mp[i]++;
n /= i;
}
}
if(n > 1) mp[n]++;
}
long long ans = 1;
for(auto p : mp){
int fi = p.first, se = p.second;
long long t = 1;
while(se--) t = (t * fi + 1) % MOD;
ans = ans * t % MOD;
}
cout << ans << endl;
return 0;
}
AcWing 872. 最大公约数
AcWing 872. 最大公约数
如果d整除a,b
d
/
a
d/a
d
/
a
d
/
b
d/b
d
/
b
那么d可以整除
d
/
(
a
x
+
b
y
)
d/(ax+by)
d
/
(
a
x
+
b
y
)
a
%
b
=
a
−
[
a
/
b
]
∗
b
=
a
−
c
∗
b
a\%b=a-[a/b]*b=a-c*b
a
%
b
=
a
−
[
a
/
b
]
∗
b
=
a
−
c
∗
b
a
%
b
=
b
%
(
a
−
c
∗
d
)
a\%b=b\%(a-c*d)
a
%
b
=
b
%
(
a
−
c
∗
d
)
a
%
b
=
b
%
(
a
%
b
)
a\%b=b\%(a\%b)
a
%
b
=
b
%
(
a
%
b
)
左边的公约数,等于右边的公约数
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}

