博客

【课堂笔记】运筹学第二章：对偶问题

  • Post author:
  • Post category:其他


标题~

听说运筹学这门课挺好的，有值得一听的必要；此篇用作课堂总结、期末复习及记录。

或许与教材内容会有很大程度重复。



本系列文章主要用于笔者期末复习，行文混乱，请见谅

本章开始会适当结合一些B站网课

【运筹学】应试向基础教程



备考补充及零碎知识点

  • 对偶问题的对偶问题就是原问题
  • 矩阵表达
  • 要弄清楚矩阵



    A

    A






    A





    和



    C

    C






    C





    分别是什么

    在这里插入图片描述

  • 最好记住这几个矩阵,进而记住

    弱对偶定理

    ,

    松弛定理



弱对偶定理

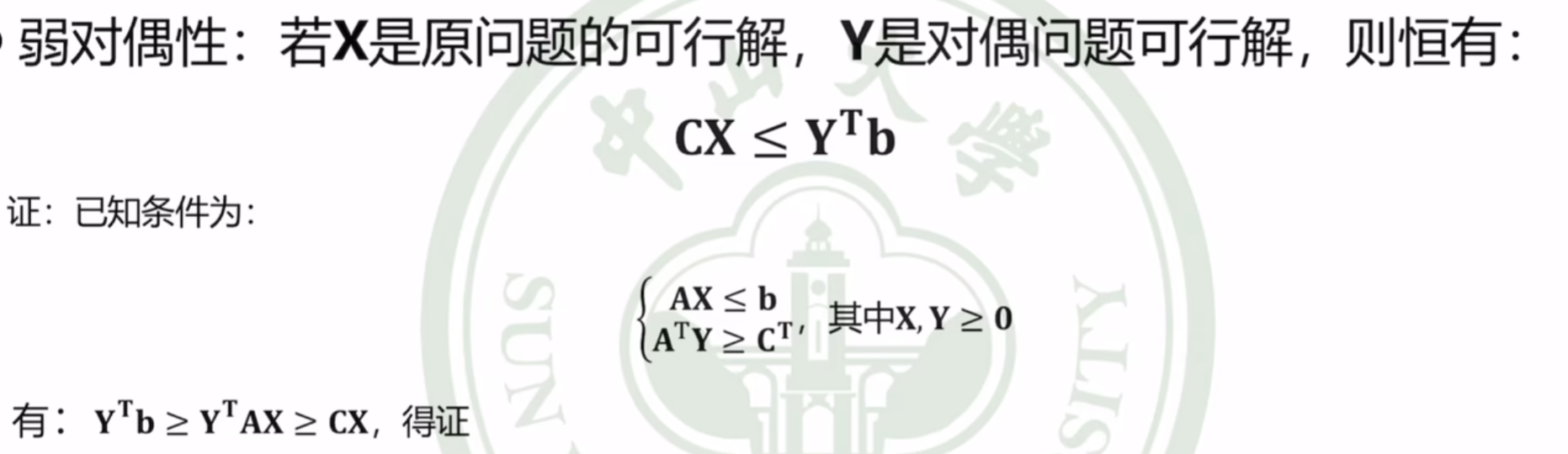
在这里插入图片描述

结合着矩阵形式表述



推论

  • 原问题最优解目标函数值是对偶问题目标函数值的

    下界

    ，对偶问题最优解目标函数值是原问题目标函数值的

    上界

    。

    对偶问题的解一定大于原问题的解

  • 原问题有无界解→对偶问题无可行解，对偶问题有无界解→原问题无可行解，但逆不成立（对偶问题无可行解时，原问题也可能无可行解)
  • 原问题有可行解而对偶问题无可行解→原问题为无界解，反之(对调”原问题”和”对偶问题”)亦然



最优性

在这里插入图片描述



强对偶定理

在这里插入图片描述



互补松弛性✨


互补松弛性

😦

双最优解情况下

）若原问题中某一约束条件对应的

对偶变量(



y

i

y_i







y










i





​















)值为非零

，则该约束条件取

严格等式

;若约束条件取

严格不等式

，则其对应的

对偶变量一定为0

，即:

  • 若



    y

    i

    >

    0

    y_{i}>\mathbf{0}







    y











    i






    ​














    >








    0





    ，则有



    ∑

    j

    =

    1

    n

    a

    i

    j

    x

    j

    =

    b

    i

    \sum_{j=1}^{n} a_{i j} x_{j}=b_{i}







    ∑











    j


    =


    1










    n






    ​















    a











    ij






    ​













    x











    j






    ​














    =









    b











    i






    ​















    ， 即松弛变量值为 0

  • 若



    ∑

    j

    =

    1

    n

    a

    i

    j

    x

    j

    <

    b

    i

    \sum_{j=1}^{n} a_{i j} x_{j}<b_{i}







    ∑











    j


    =


    1










    n






    ​















    a











    ij






    ​













    x











    j






    ​














    <









    b











    i






    ​















    ， 即松弛变量值不为 0 ，则有



    y

    i

    =

    0

    y_{i}=0







    y











    i






    ​














    =








    0






证明过程(推荐看一看)

在这里插入图片描述



换言之:对偶变量和松弛变量的乘积为0



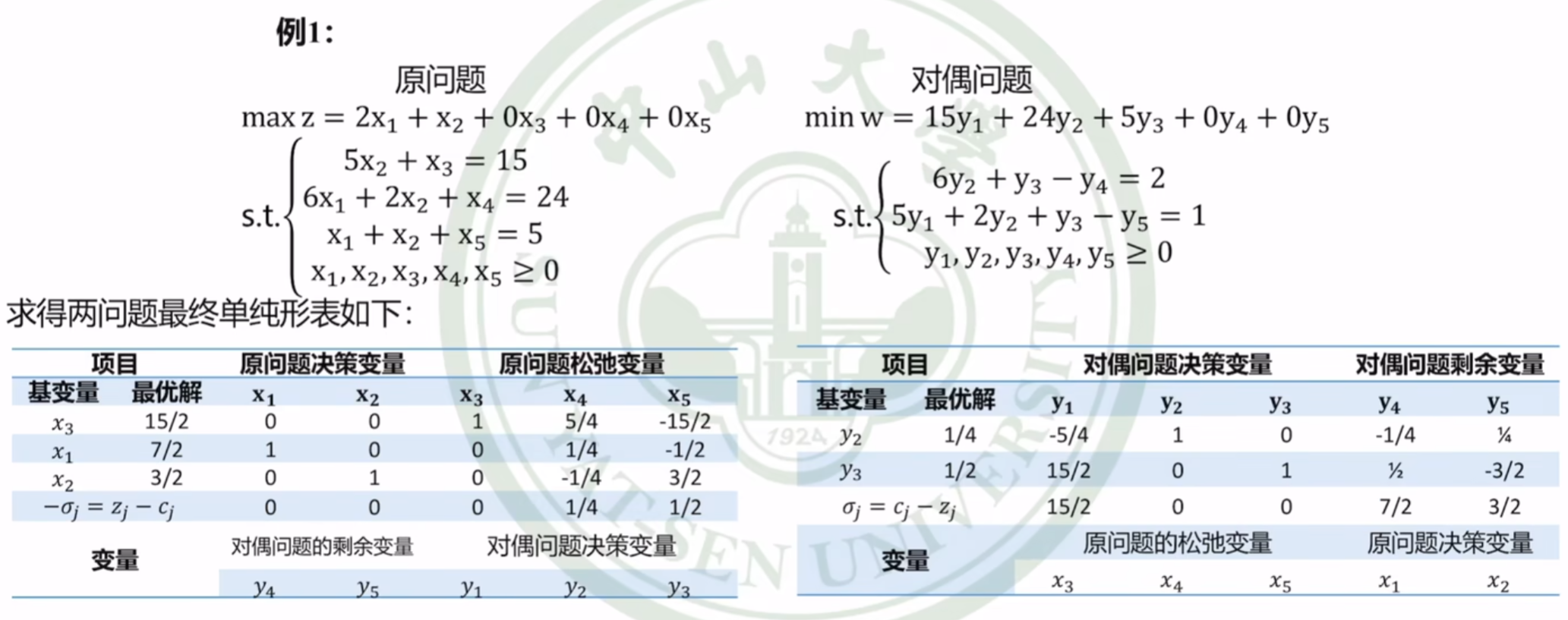
例子

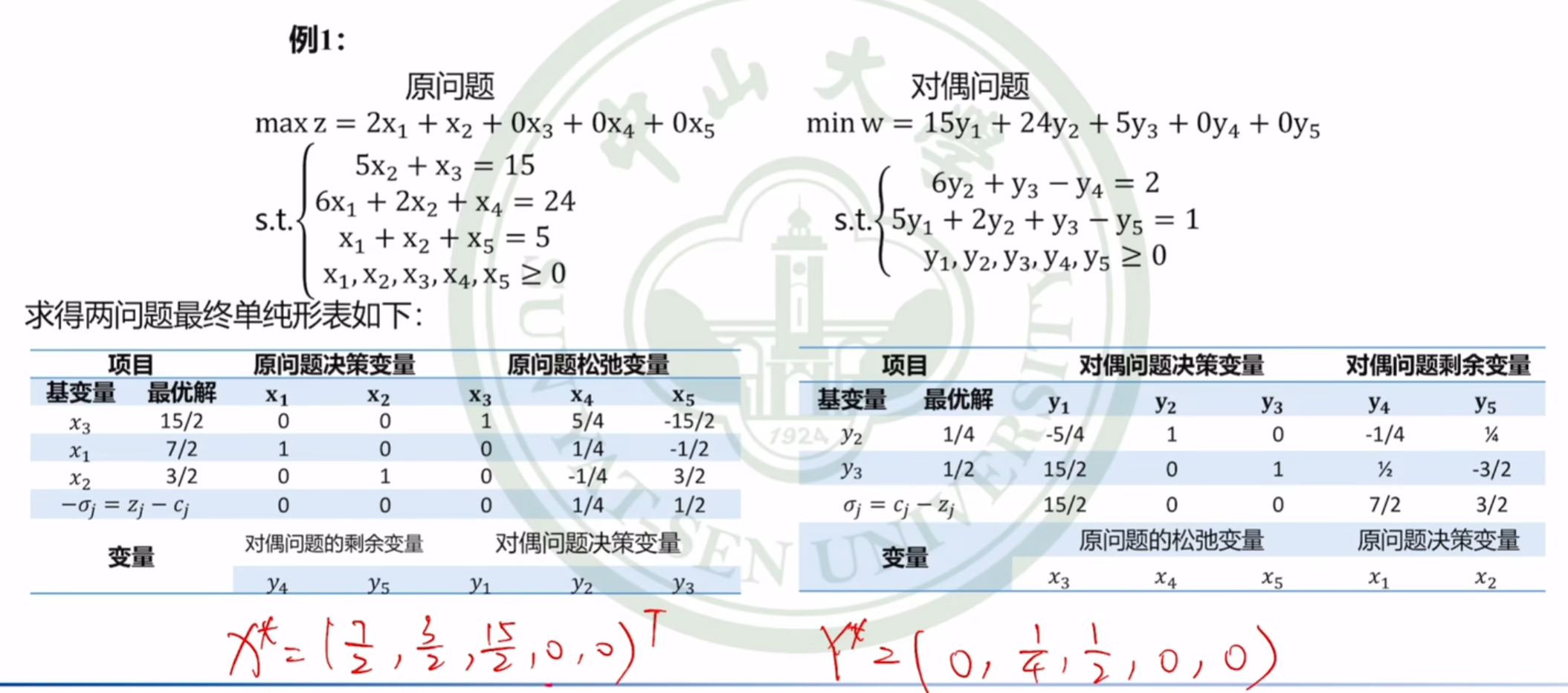
在这里插入图片描述

本题中,



y

1

y_1







y










1





​















为0,对应第一个松弛变量



x

3

x_3







x










3





​















不为0




y

2

,

y

3

y_2,y_3







y










2





​












,





y










3





​















不为0,对应第二第三个松弛变量



x

4

,

x

5

x_4,x_5







x










4





​












,





x










5





​















不为0



应用

知道了对偶表的最终表,就知道了飞机变量,从而知道了基变量.



影子价格



定义

单位第



i

i






i





种资源在最优方案中做出贡献的估价

做法:通过

求导

得到每一种资源带来的利润的提升是多少



内涵

资源的影子价格有赖于资源的利用情况，即当目前一组基变量用于获得原问题最优解时，对偶变量



y

i

y_i







y










i





​















每单位对利润的贡献。（需要区别于资源的市场价格)

在这里插入图片描述

根据

互补松弛性质

,有如下结论:

  • 第i种资源未充分利用→其边际价格为0
  • 第i种资源的边际价格不为0→其已耗尽



注意

当出现退化的最优解时，会出现第i种资源恰好耗尽，而非稀缺，但其影子价格



y

i

y_i







y










i





​















仍大于0的情况(对应



y

i

y_i







y










i





​















的第i个约束条件的松弛变量取值为0)，此时



b

i

b_i







b










i





​















值的任何增加只会带来该种资源的剩余，而不增加利润值。

比如 这种值正好耗尽,同时其他值也耗尽了,这时候只增加这个值,没有用!



问题

什么叫退化的最优解



检验数的意义

在这里插入图片描述



问题

为什么



y

i

=

C

B

B

−

1

y_i=C_BB^{-1}







y










i





​














=









C










B





​













B











−


1














附上课件的解答,这个我也不知道为什么

在这里插入图片描述



问题：什么是退化的最优解



对偶问题的引入

所有问题一定能找到对偶问题，但是其对偶问题不一定有意义.

在这里插入图片描述



从另一个角度思考

假设

公司A

想要收购这家公司的全部资源A、B、C自己生产

从

公司A

的角度思考：


公司A

的获利最大化——目标（以最小代价收购）

这家公司愿意出让这些资源——约束（出让所得不小于原有盈利）

以



y

1

,

y

2

,

y

3

y_1,y_2,y_3







y










1





​












,





y










2





​












,





y










3





​















表示A、B与C三种资源的出让代价，

在这里插入图片描述



总结

原问题 对偶问题
收益最大化 代价最小化
方程的个数,即种类的个数 决策变量数
价值系数 对偶问题右端的项向量,即

约束
资源的

约束
 		价值系数



对偶问题的一般形式



原问题

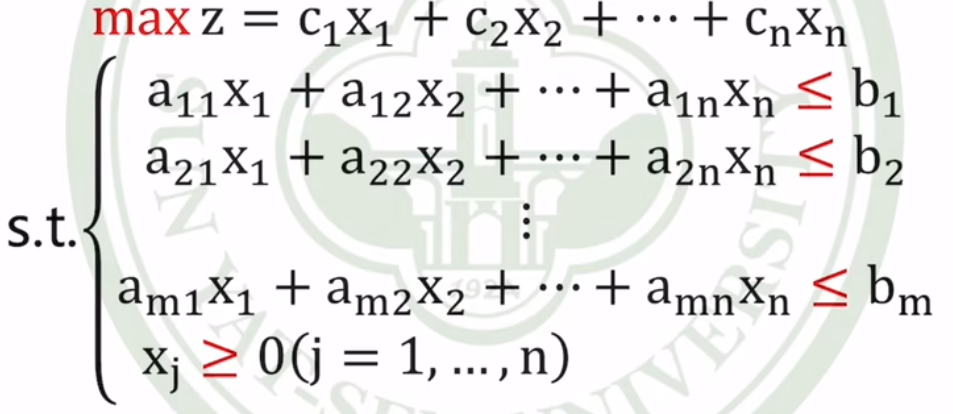
在这里插入图片描述



对偶问题

用



y

i

(

i

=

1

,

2…

m

)

y_i(i=1,2…m)







y










i





​












(


i




=








1


,




2…


m


)





表示第



i

i






i





种资源的估价

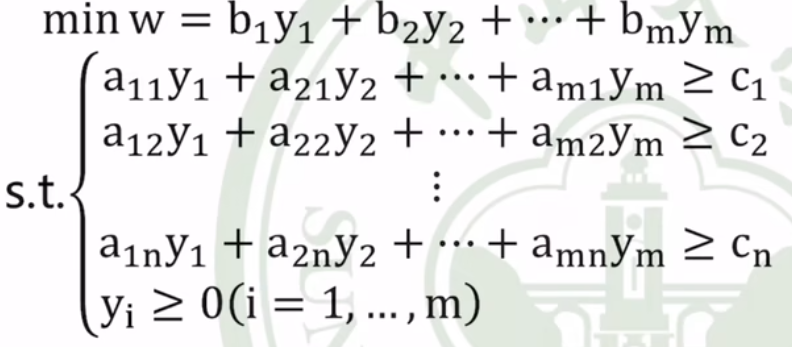
在这里插入图片描述



✨以矩阵描述(更加直观)

在这里插入图片描述



多做题,就知道什么是对偶了



对称形式

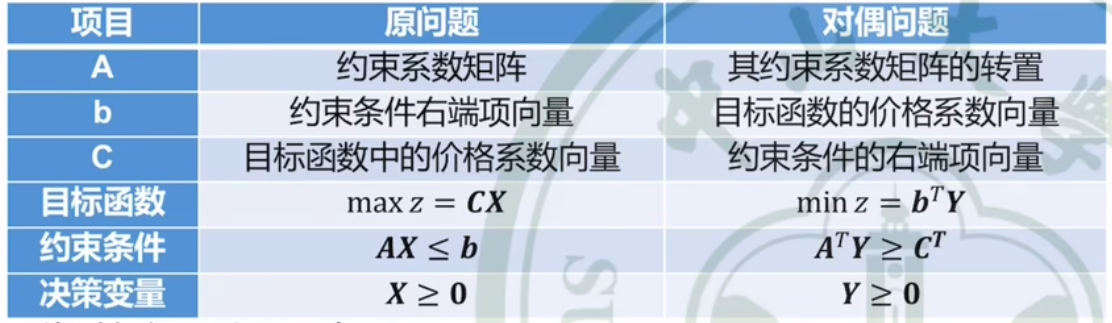
在这里插入图片描述

与前面内容有所重复,

即



B

,

C

B,C






B


,




C





互换,



A

A






A





转置

上面讲的都是对称形式



非对称形式✨✨✨【一定要掌握】

转化有一定的规律,下面是详细的推导过程

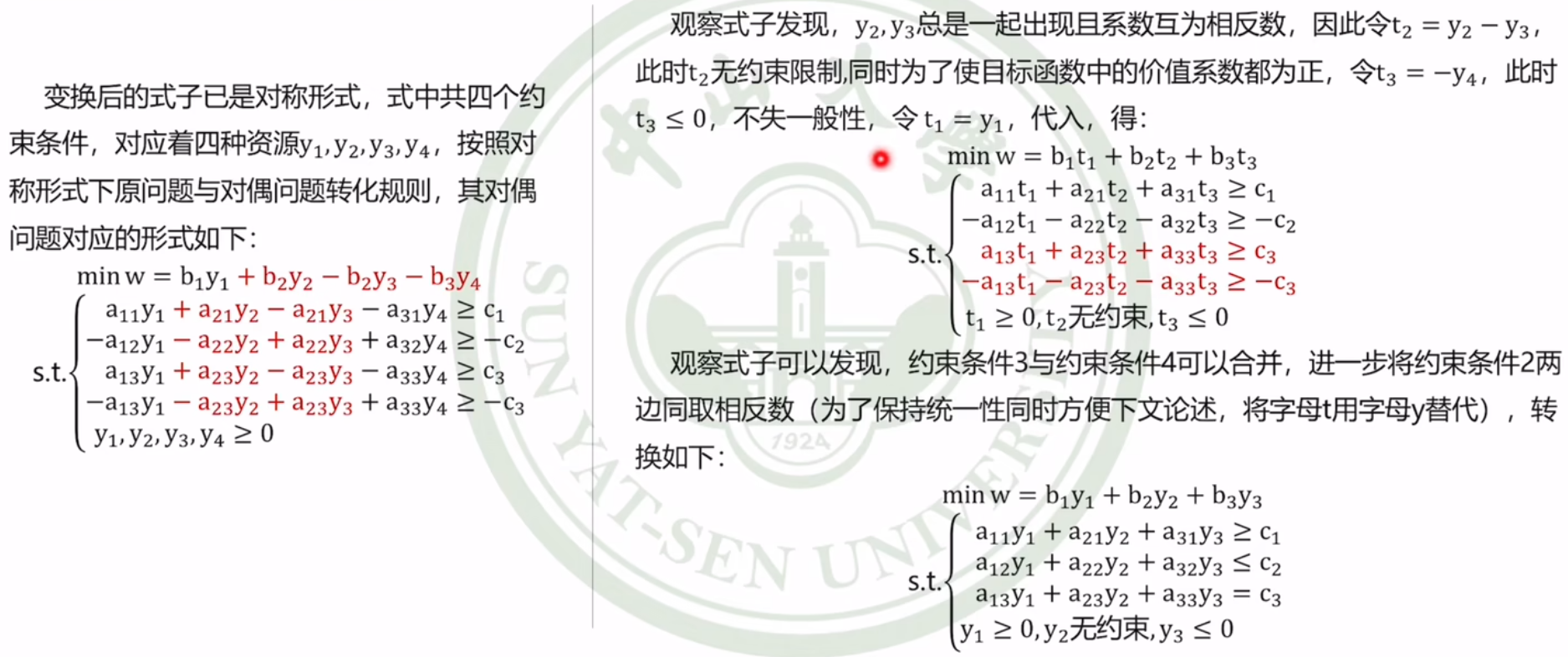
在这里插入图片描述

在这里插入图片描述



规律

类似对称形式的,

约束条件的符号

决定了

变量

,

变量的符号

决定了

约束条件


⚠️注意我们说的是max向min转化的问题

⚠️如果反过来,那么最后两行的”

变号

” ”

不变号

“也要对调.

在这里插入图片描述



推导过程



复习单纯形法计算过程

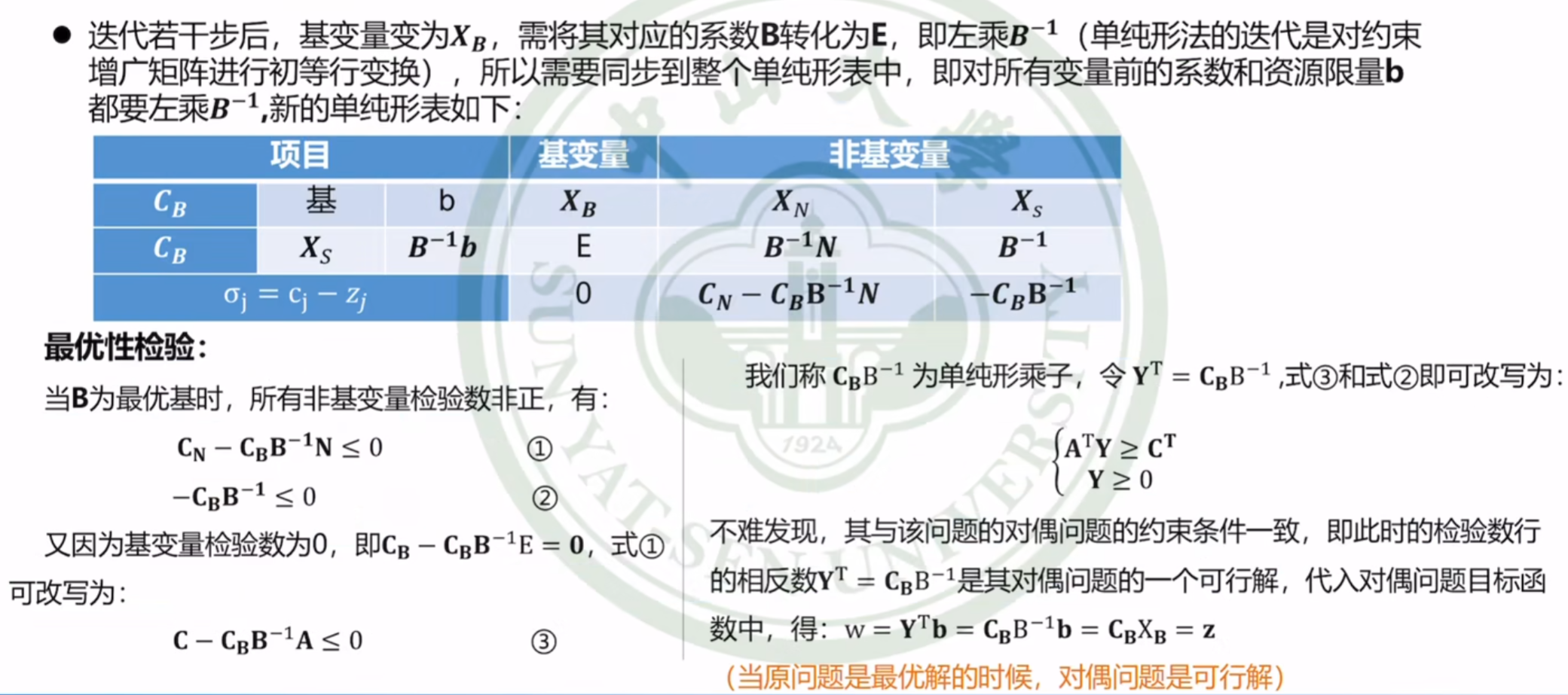
在这里插入图片描述

在这里插入图片描述

为了防止这个地方听不懂,做一点说明:

检验数:




σ

j

=

c

j

−

z

j

=

c

j

−

C

B

B

−

1

P

j

\sigma_{\mathrm{j}}=\mathrm{c}_{

{j}}-z_{j} =c_j – {C}_{\mathrm{B}}B^{-1}P_j \quad







σ











j






​














=









c












j







​














−









z











j






​














=









c










j





​














−










C












B






​













B











−


1











P










j





​



















其中P是第



j

j






j





列变量前的系数(参考第一章)

  • 考虑所有基变量的列:前m列所有



    P

    j

    P_j







    P










    j





    ​















    合起来就变成了矩阵



    B

    B






    B






    所以检验数:



    C

    B

    −

    C

    B

    B

    −

    1

    P

    j

    =

    C

    B

    −

    C

    B

    B

    −

    1

    B

    =

    0

    {C}_{\mathrm{B}} – {C}_{\mathrm{B}}B^{-1}P_j={C}_{\mathrm{B}} – {C}_{\mathrm{B}}B^{-1}B=0








    C












    B






    ​














    −










    C












    B






    ​













    B











    −


    1











    P










    j





    ​














    =










    C












    B






    ​














    −










    C












    B






    ​













    B











    −


    1










    B




    =








    0




  • 考虑所有飞机变量中的



    X

    N

    X_N







    X










    N





    ​















    列:这些列合起来变成了矩阵



    N

    N






    N






    所以同理,检验数:



    C

    N

    −

    C

    B

    B

    −

    1

    N

    {C}_{\mathrm{N}} – {C}_{\mathrm{B}}B^{-1}N








    C












    N






    ​














    −










    C












    B






    ​













    B











    −


    1










    N




  • 考虑松弛变量



    X

    S

    X_S







    X










    S





    ​















    ,松弛变量的价值系数为0,则有

    检验数:



    0

    −

    C

    B

    B

    −

    1

    E

    =

    −

    C

    B

    B

    −

    1

    0- {C}_{\mathrm{B}}B^{-1}E=- {C}_{\mathrm{B}}B^{-1}






    0




    −










    C












    B






    ​













    B











    −


    1










    E




    =








    −




    C












    B






    ​













    B











    −


    1












剩下的,见小字部分:

推导出了②③式,然后换元



举例说明

在这里插入图片描述



对偶单纯形法



单纯形法基本思路

先寻找到

初始基可行解

，判断所有检验数是否小于等于0。若是，查看基变量中是否有人工变量，若无非零人工变量，即找到了最优解;若为否，再找出相邻目标函数值更大的基可行解，并继续判别，直到

找出最优解

。



❓问题：怎么（什么时候）添加人工变量



❓问题：有非零人工变量怎么办



对偶单纯形法基本思路

同样的，先找对偶问题的可行解再找对偶问题最优解

  • 最优性看检验数



    σ

    j

    \sigma_j







    σ










    j





    ​














  • 可行性看右端项



    b

    i

    b_i







    b










    i





    ​
















确定初始基解

与单纯形法不同，

并不要求资源限量



b

i

b_i







b










i





​















为正



但是，当所有



b

i

b_i







b










i





​















为正，意味着原问题取到可行解，那么此时原问题和对偶问题得到的都是最优解


在这里插入图片描述

  • 先确定出基，是b里最小的



问题 为什么对偶问题的最优性一直都是满足的



跟单纯形法的区别与联系✨✨

  • 单纯形法

    先确定入基

    变量，是

    最大的检验数

    (检验数：基变量一定为0,一部分小于零一部分大于零)，对偶

    先确定出基

    变量，是

    最小的



    b

    (

    b

    <

    0

    )

    b(b<0)






    b


    (


    b




    <








    0


    )






    【单纯形法先列后行，对偶单纯形法先行后列】

    ✨✨🙌检验数



    σ

    \sigma






    σ





    非正，代表对偶问题有可行解；左边的b非负，代表原问题有可行解。

  • 单纯形法随后确定

    出基变量

    ，是检验数



    θ

    i

    =

    b

    i

    j

    a

    i

    \theta_i=\frac{b_{ij}}{a_i}







    θ










    i





    ​














    =





















    a










    i





    ​



























    b











    ij






    ​
















    ​

















    中

    最小的

    ，【零和负数忽略！】；对偶单纯形法

    确定入基变量

    ，选择



    θ

    =

    min

    ⁡

    {

    c

    j

    −

    z

    j

    a

    r

    j

    ∣

    a

    r

    j

    <

    0

    }

    =

    c

    s

    −

    z

    s

    a

    r

    s

    \theta=\min \left\{\frac{c_{j}-z_{j}}{a_{r j}} \mid a_{r j}<0\right\}=\frac{c_{s}-z_{s}}{a_{r s}}






    θ




    =








    min






    {

















    a











    r


    j






    ​



























    c











    j






    ​












    −



    z











    j






    ​
















    ​
















    ∣





    a











    r


    j






    ​














    <




    0



    }






    =





















    a











    rs






    ​



























    c











    s






    ​












    −



    z











    s






    ​
















    ​


















    最小的

    【零和正数忽略！】【先算出



    σ

    \sigma






    σ





    再算出



    θ

    \theta






    θ





    的】【



    z

    s

    z_s







    z










    s





    ​















    就是每一行



    C

    B

    i

    ∗

    a

    i

    s

    C_{Bi}*a_{is}







    C











    B


    i






    ​














    ∗









    a











    i


    s






    ​
















    求和的值

    】

    【对偶单纯形法中的



    σ

    \sigma






    σ





    和



    b

    b






    b





    跟原单纯形法是

    相反的

    ，所以事实上是一样的】

  • 单纯形法中最后判断的方式是检验

    数



    σ

    \sigma






    σ





    全部小于等于零

    ，而

    始终保证



    b

    i

    b_i







    b










    i





    ​















    全部大于等于零

    ；而对偶单纯形法相反，最后判断的

    是



    b

    i

    b_i







    b










    i





    ​















    是否全部大于等于零

    ，始终保证

    检验数



    σ

    \sigma






    σ





    全部小于等于零

    。⚠️⚠️⚠️⚠️

  • 【在后面做题时发现，上面这些条件需要原问题为{min，大于等于}，并且最后转换为max的问题】



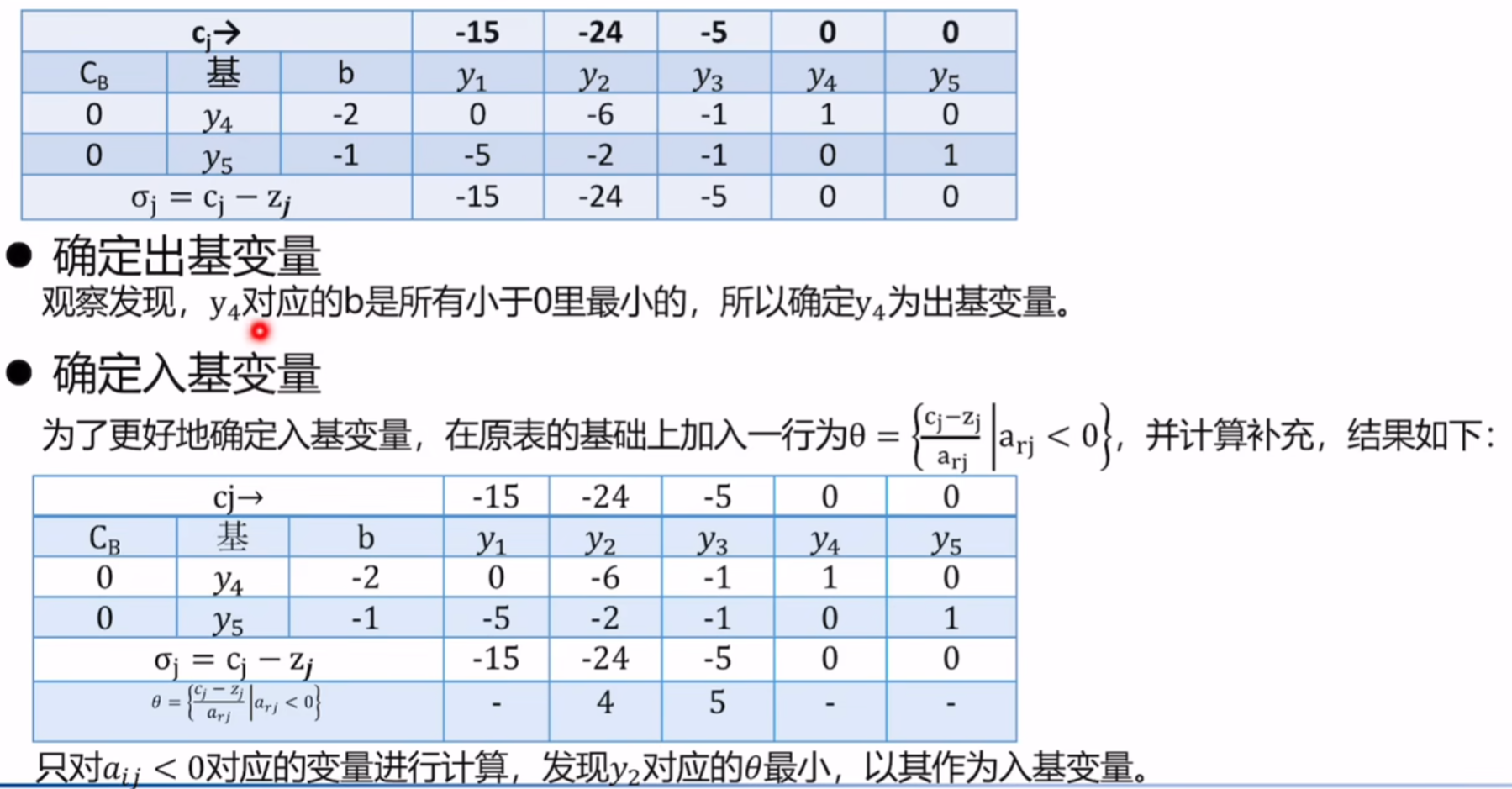
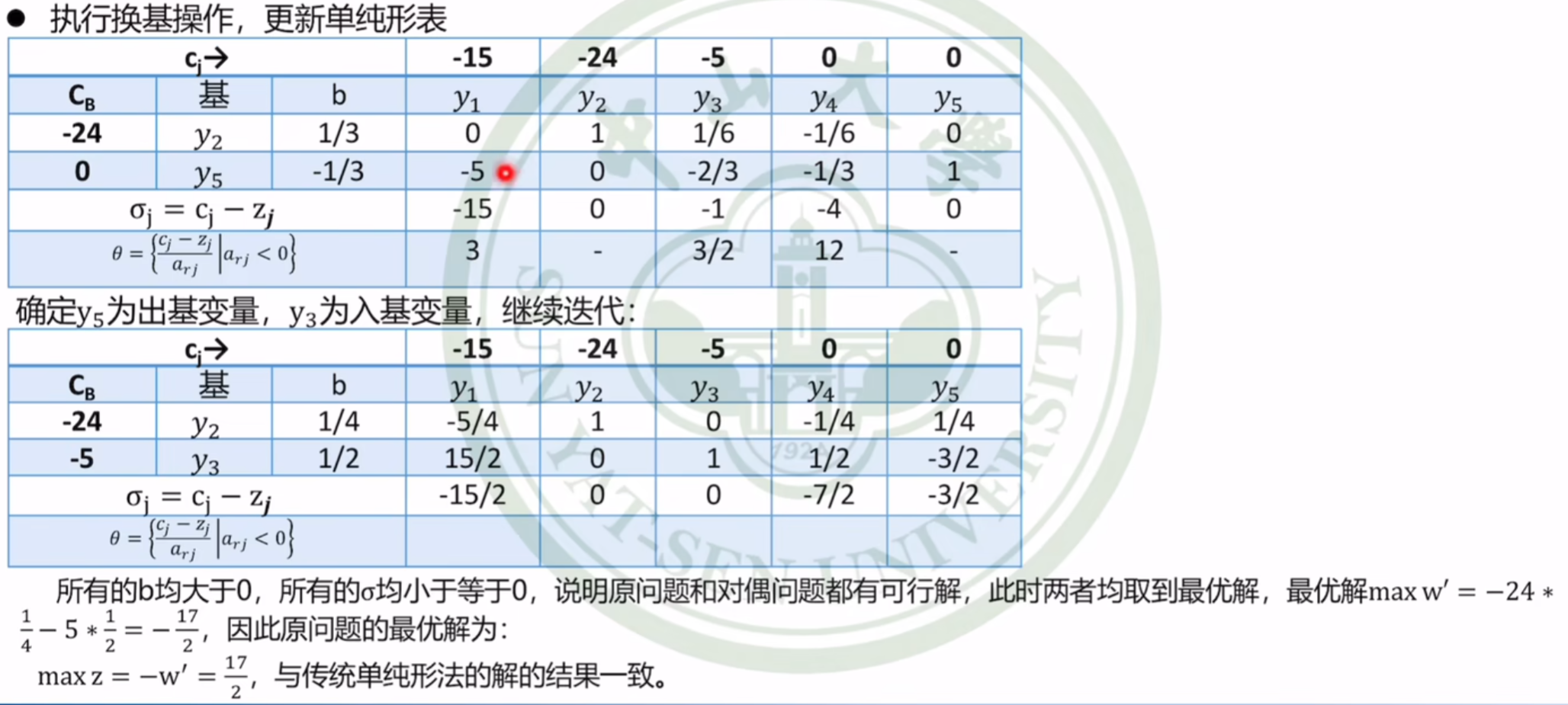
例题讲解✨✨🙌



注意看，对偶单纯形法的条件是min还是max【我看到的是min配合大于等于】



注意：对偶问题不需要用对偶表，看视频就好⚠️⚠️⚠️⚠️

在这里插入图片描述

在这里插入图片描述


https://www.bilibili.com/video/BV12Z4y1W7aU



https://www.bilibili.com/video/BV1ut4y1T7K2



下面的例题做法非考试正规做法！！但是求单纯形法规则是一样的

在这里插入图片描述

对偶问题为：

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述



运输问题建模

【考试一般不考原理，要考原理考的也是单纯形法】

【运输问题的思路其实也是单纯形法，但是针对这类问题进行了优化】



产销平衡问题



建立模型

在这里插入图片描述

这还是线性规划问题，可以用单纯形法求解，但是变量太多了，有另外的求解方法。


这种方法本质上和单纯形法一样，也是先找可行解在迭代出最优解。


  • 模型特点
  1. 解有上下界
  2. 产销平衡（有一个多余约束条件）
  3. 约束条件比较特殊

  • 运输表


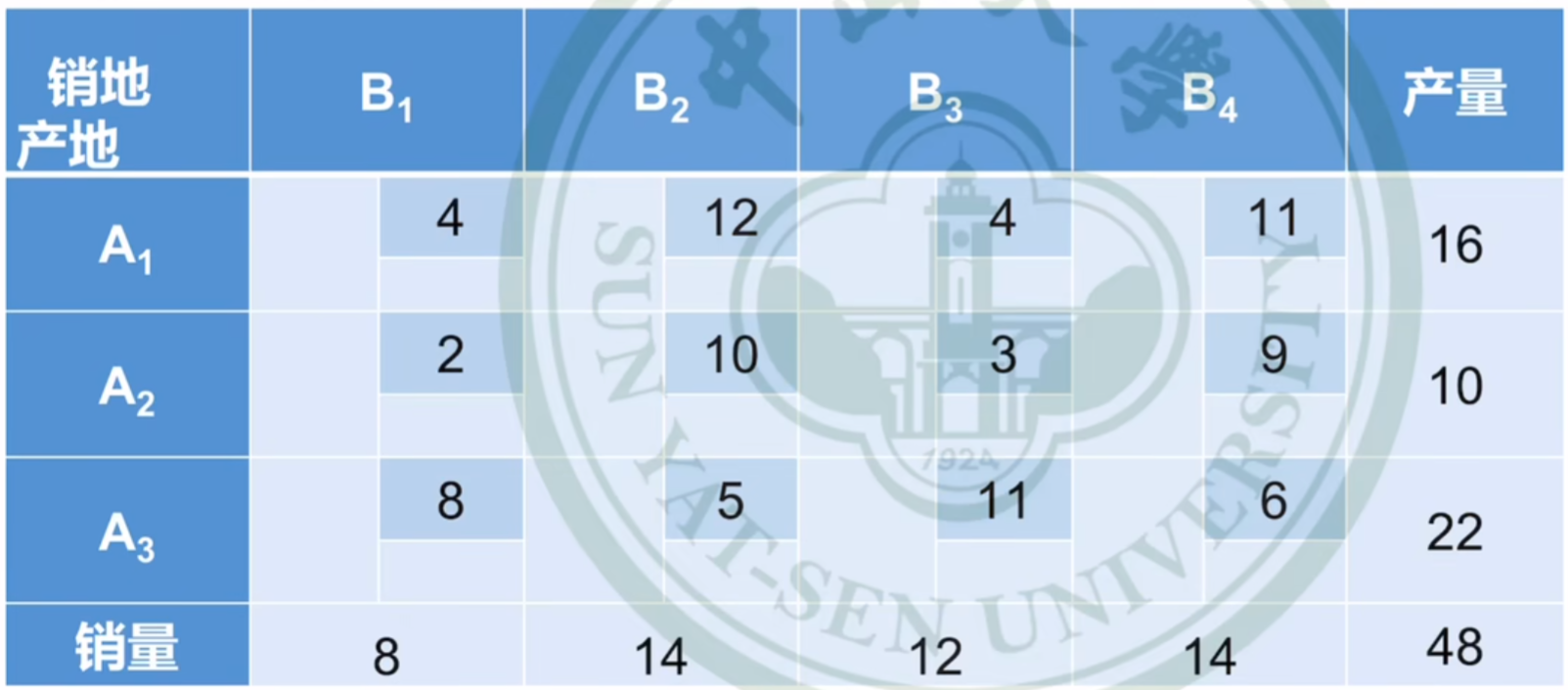
    在这里插入图片描述

    本题有



    3

    +

    4

    −

    1

    =

    6

    3+4-1=6






    3




    +








    4




    −








    1




    =








    6





    个这个表应该有



    m

    +

    n

    −

    1

    m+n-1






    m




    +








    n




    −








    1





    个基变量，剩下的是非基变量



求解模型【表上作业法】



确定可行解方法①：左上角填充法

尽可能使左上角取得最大值

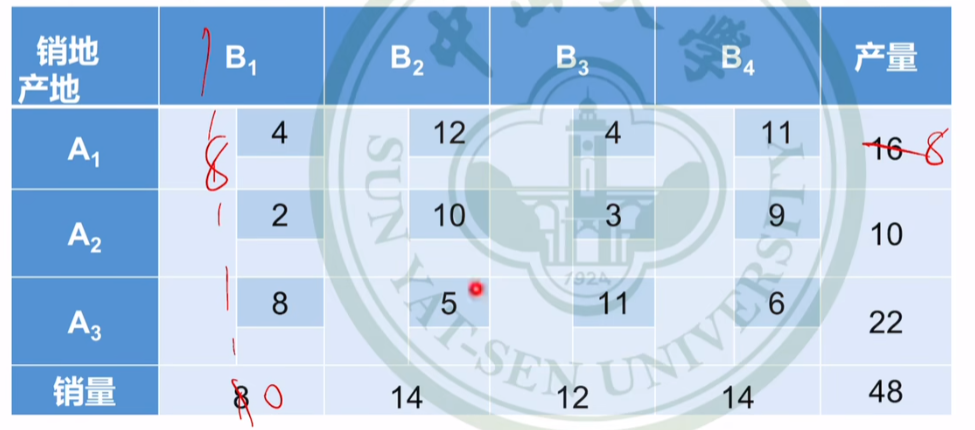
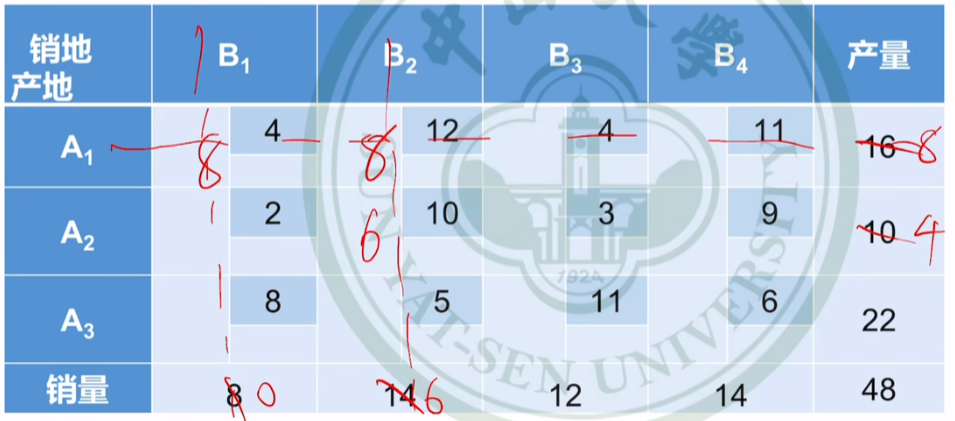
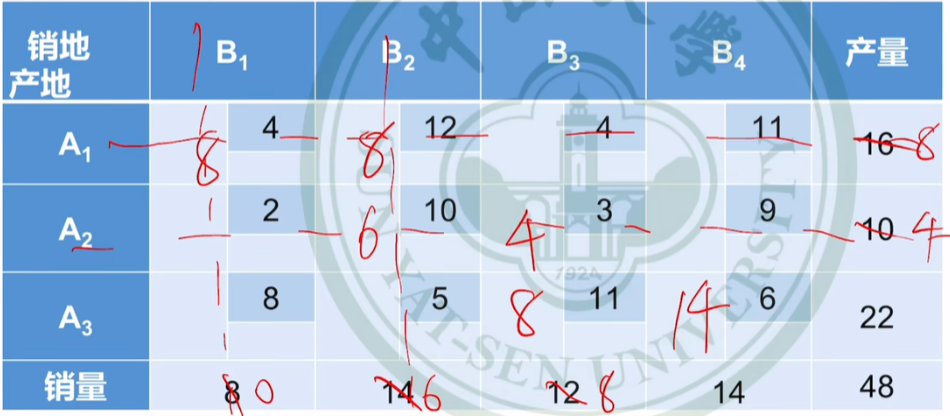
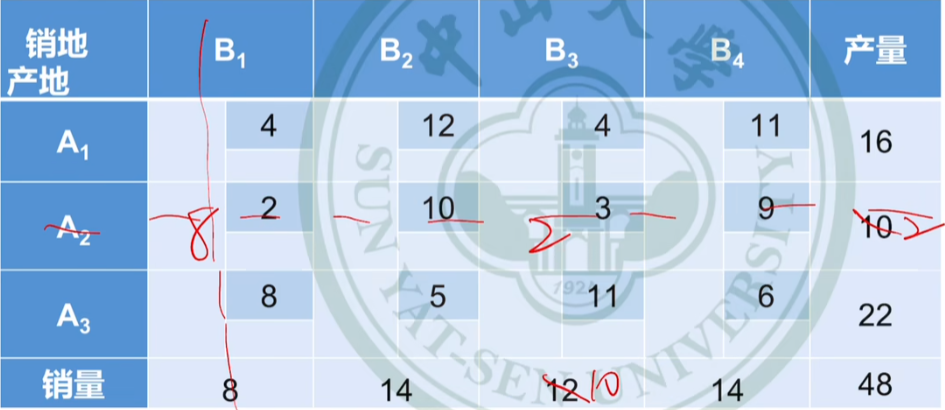
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述



确定可行解方法②：最小元素法

每一步优先考虑单位运价最小的业务【范围是在整个表里找最小运费】

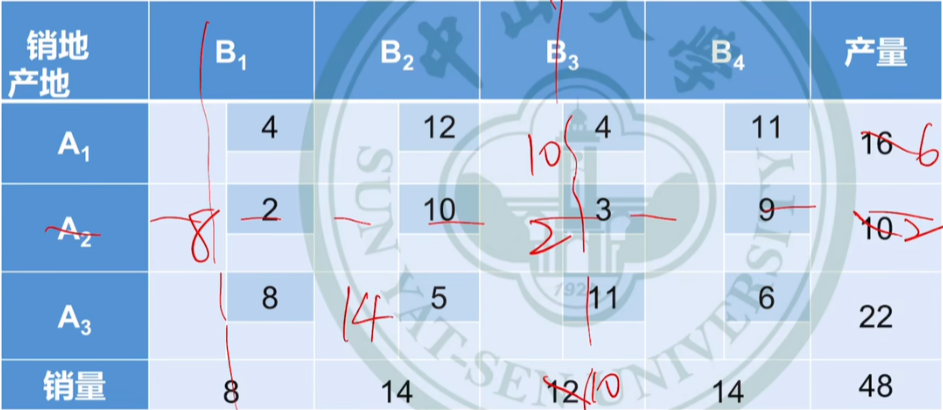
在这里插入图片描述

在这里插入图片描述



确定可行解方法③：沃格尔法

在这里插入图片描述

找运价最小与次小，二者之差称为

罚数

，优先选择

最大的罚数


在这里插入图片描述

在这里插入图片描述



迭代方法①：闭回路法



入基变量选择


选择检验数最小【负数绝对值中最大的那个】


  • 核心

    ：从非基变量开始，构造回路

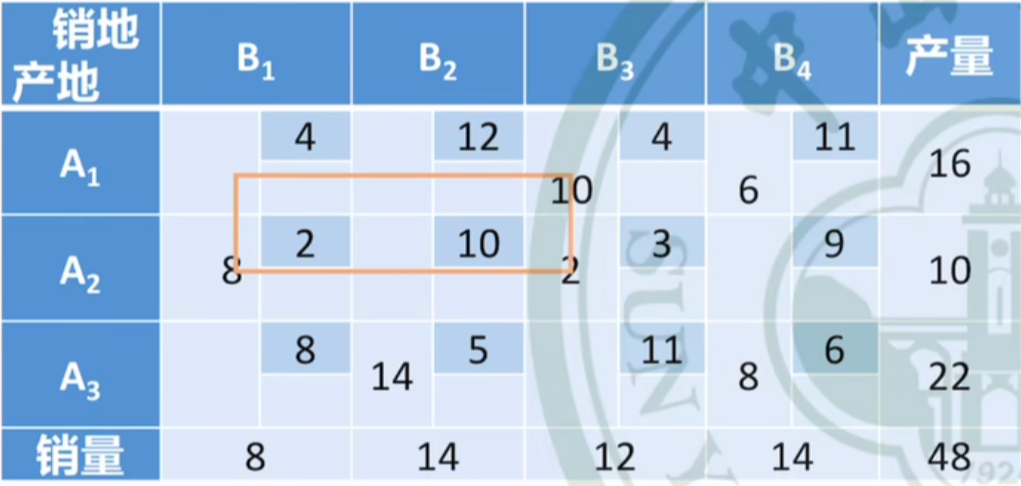
    在这里插入图片描述

  • 原理

    ：令起始的

    非基变量

    为1，（按照顺时针或者逆时针都可以）为了保证产销平衡的约束条件，下一个

    基变量

    减1，再下一个

    基变量

    加1，该格子检验数为

    这一变化带来的运费变化

  • 即

    ：遇到空格保持直走，遇到基变量

    可以选择

    90°拐弯，最后计算这一个非基变量对运费带来的变化。所有的非基变量都要算出来，取

    最小的入基

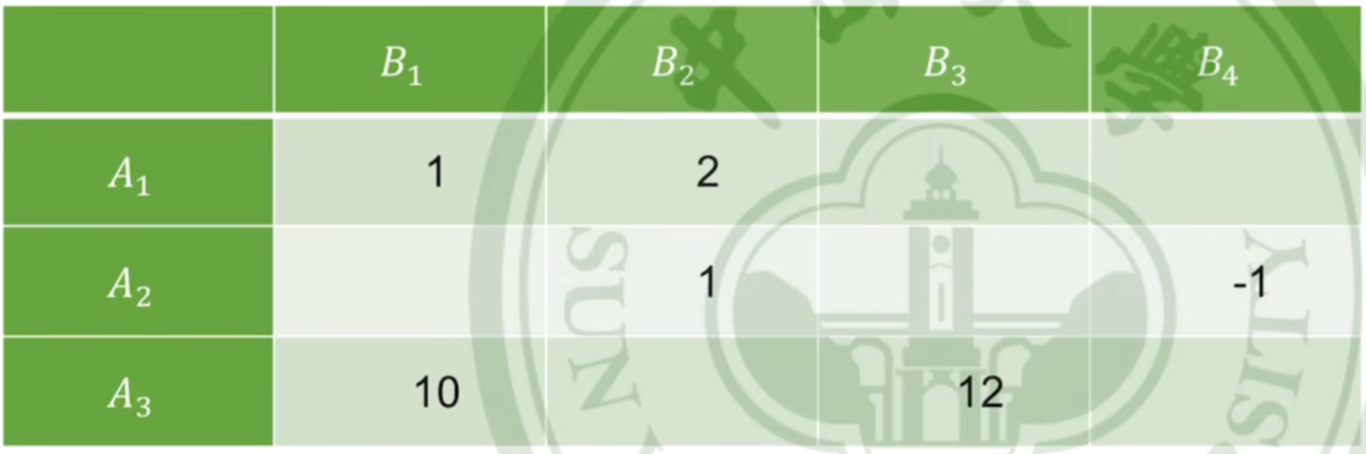
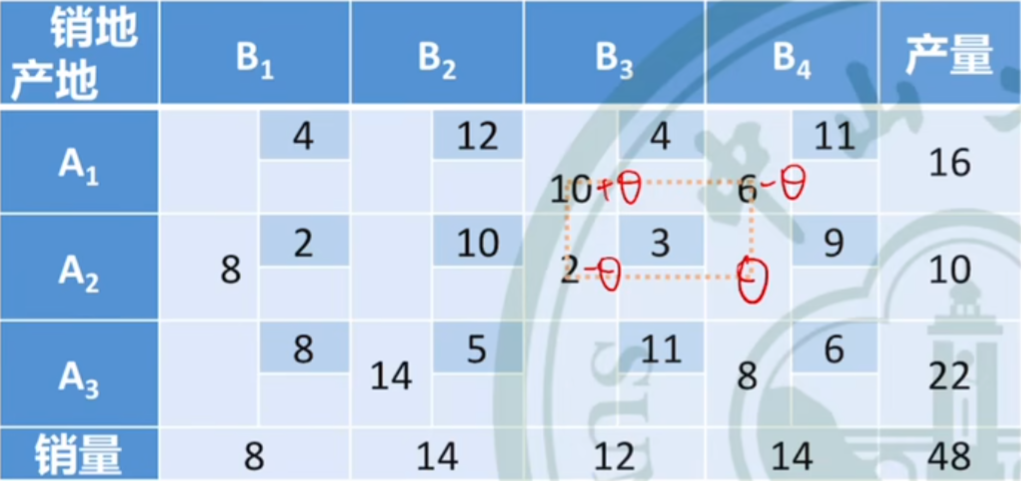
在这里插入图片描述



出基变量选择

画出入基变量的回路，如图所示，回路中

偶数点最小的基变量

最先变成0

【思路是让某个基变量变成0，如题，此时



θ

\theta






θ





取2】

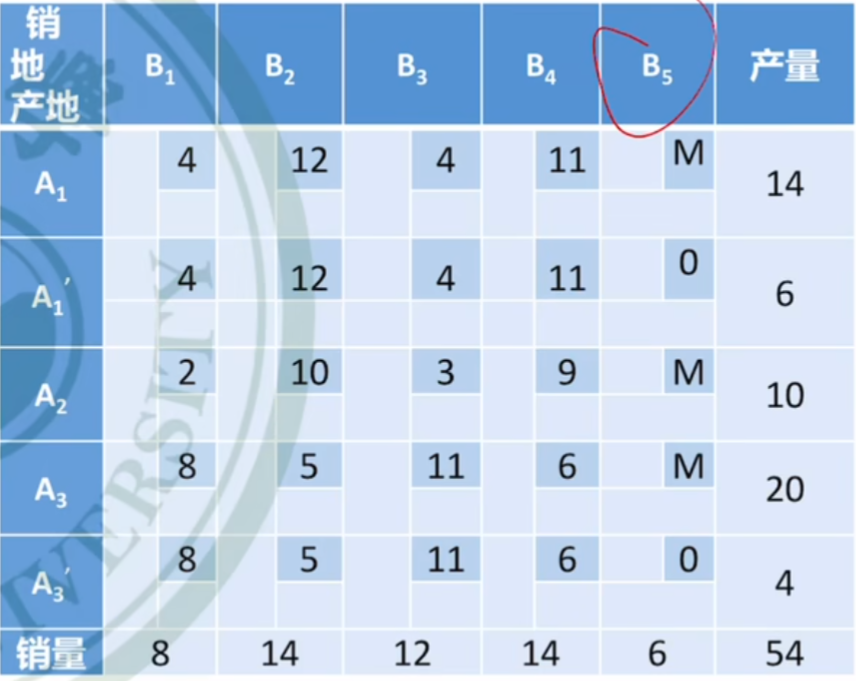
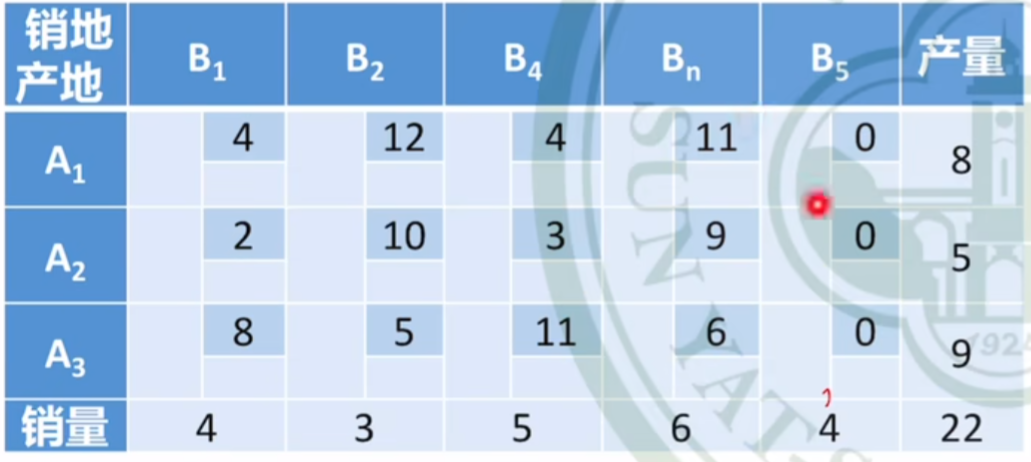
在这里插入图片描述





产销不平衡问题



产量大于销量

对于这类问题，可以

假想一个销地




B

5

B_5







B










5





​















，对于产量大于销量的这部分，统一运往



B

5

B_5







B










5





​















。

由于



B

5

B_5







B










5





​















是个假想地，实际上就是

就地存储

在A;的物品数量，因此其运价为

0

，新的单位运价表如下:

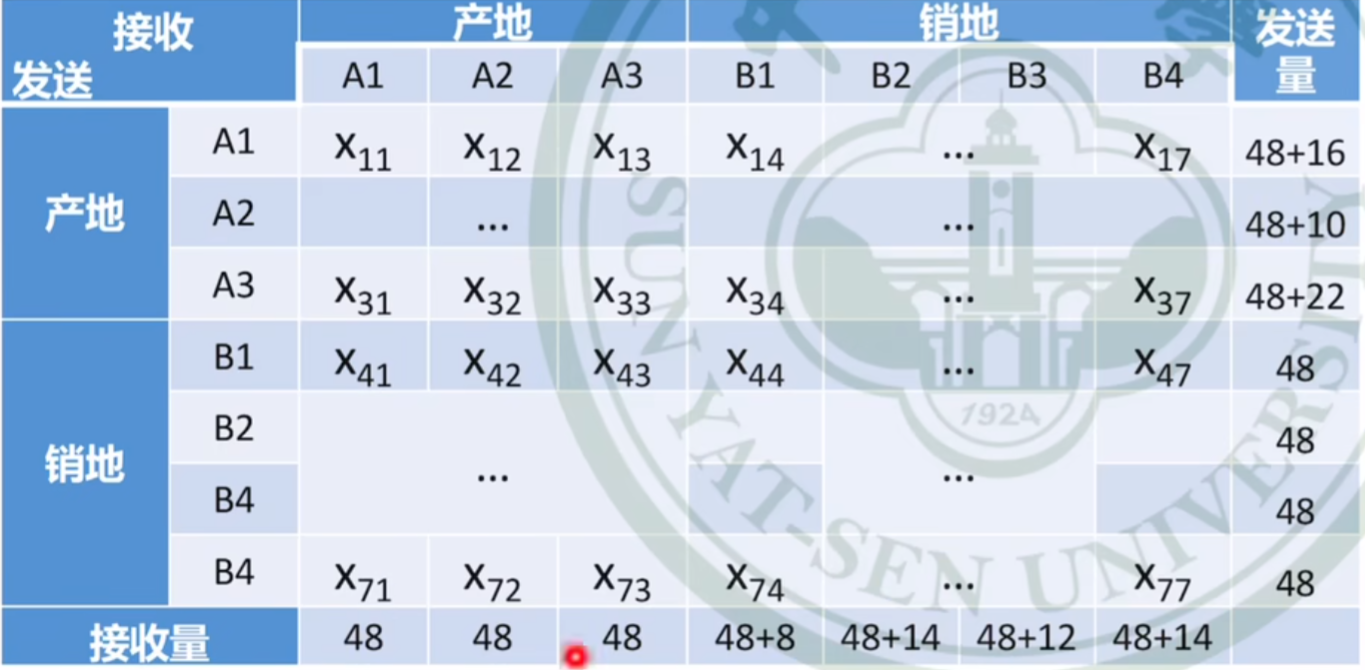
在这里插入图片描述



有转运的问题

产地同时也是销地

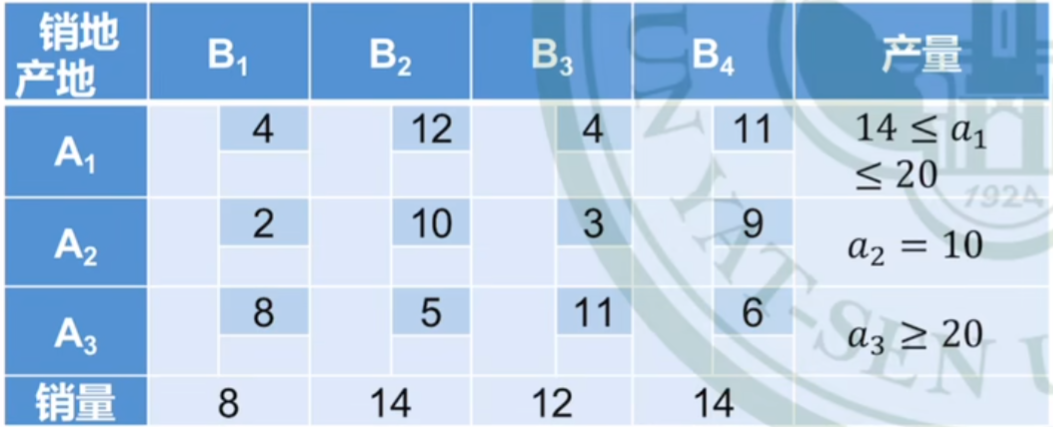
在这里插入图片描述



产销不确定

在这里插入图片描述

分析：

  • 首先，



    a

    3

    a_3







    a










    3





    ​















    是有上限的

  • 将产量分为

    最小产量

    和

    冗余产量

    ，分别放在



    A

    i

    A_i







    A










    i





    ​















    和



    A

    i

    ′

    A_i^{‘}







    A










    i





















    ′














    ​















    【必须到/可到可不到】

  • 假定一个不能被运输的销地，销量由产量减已有销量得到。【



    A

    i

    ′

    A_i^{‘}







    A










    i





















    ′














    ​















    这种

    可到可不到

    的放到B5相当于

    原地储存

    】

    在这里插入图片描述


版权声明：本文为weixin_51772802原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。