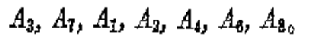一、 欧拉图
1.定义
设G是无孤立结点的图,若存在一条路(回路),经过图中每边一次且仅一次,则称此路(回路)为该图的一条欧拉路(回路)。
具有欧拉回路的图称为欧拉图。
规定:平凡图为欧拉图。
以上定义既适合无向图,又适合有向图。
2.欧拉图的判定
定理 无向图G = <V, E>具有一条欧拉路,当且仅当G是连通的,且仅有零个或两个奇度数结点。
结论:
推论 无向图G = <V, E>具有一条欧拉回路,当且仅当G是连通的,并且所有结点的度数均为偶数。
定理 有向图G具有一条单向欧拉路,当且仅当G是连通的,且除了两个结点以外,其余结点的入度等于出度,而这两个例外的结点中,一个结点的入度比出度大1,另一个结点的出度比入度大1。
推论 有向图G具有一条单向欧拉回路,当且仅当G是连通的,且所有结点的入度等于出度。
3.Fleury算法
求欧拉图G = <V, E>的欧拉回路的Fleury算法:
(1)任取v0∈V,令P0 = v0,i = 0;
(2)按下面的方法从E-{e1, e2, …, ei}中选取ei+1:
a. ei+1与vi相关联;
b. 除非无别的边可选取,否则ei+1不应该为
G’ = G-{e1, e2, …, ei}中的桥;
(3)将边ei+1加入通路P0中,
令P0 = v0e1v1e2…eiviei+1vi+1,i = i+1;
(4)如果i = |E|,结束,否则转(2)。
4.欧拉图的总结
(1)仅有欧拉路而无欧拉回路的图不是欧拉图;
(2)图中是否存在欧拉路、欧拉回路的判定非常简单,只需要数一下图中结点的度数即可;
(3)使用Fleury算法求欧拉路(回路)时,每次走一条边,在可能的情况下,不走桥。
二、 汉密尔顿图
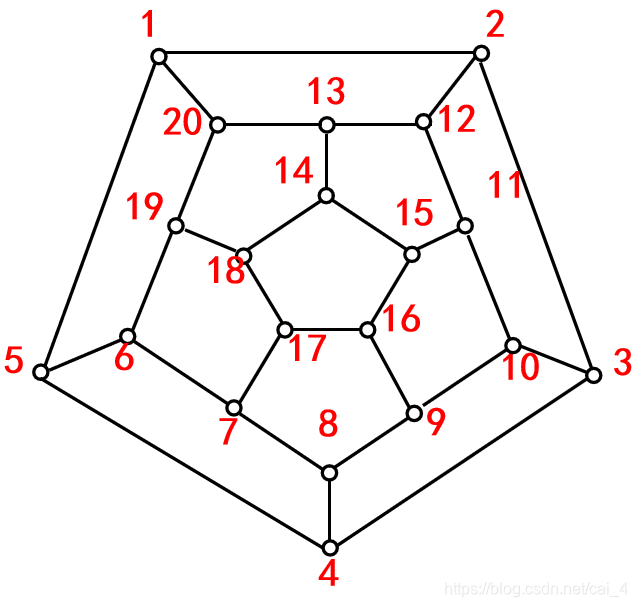

在图中,删除结点子集{a, b, c, d, e},得到的图有7个连通分支,由定理知,该图不是汉密尔顿图,因而不会存在汉密尔顿回路。
经过图中每个结点一次且仅一次的路(回路)称为汉密尔顿路(回路)。
存在汉密尔顿回路的图称为汉密尔顿图。
规定:平凡图为汉密尔顿图。
以上定义既适合无向图,又适合有向图。
2.汉密尔顿图的判定
判定:Dirac定理(充分条件)
设一个无向图中有N个顶点,若所有顶点的度数大于等于N/2,则哈密顿回路一定存在.(N/2指的是⌈N/2⌉,向上取整)
定理 设图G = <V, E>是汉密尔顿图,V1是V的任意非空子集,则
W(G-V1) ≤ |V1|
其中W(G-V1)是从G中删除V1后所得图的连通分支数。(必要条件)
推论:设图G = <V, E>中存在汉密尔顿路,则对V的任意非空子集V1,都有
W(G-V1) ≤ |V1| + 1
定理:设G = <V, E>是具有n个结点的简单图。如果G中每一对结点u, v∈V的度数,均有
deg(u)+deg(v)≥n-1
则G中存在汉密尔顿路。(充分条件)
推论:推论 设G = <V, E>是具有n个结点的简单图。如果对任意两个结点u, v∈V,均有
deg(u)+deg(v)≥n,n为结点数
则G中存在汉密尔顿回路。
需要注意,定理给出的是汉密尔顿图的充分条件,而不是必要条件。在六边形中,任两个不相邻的结点的度数之和都是4<6,但六边形是汉密尔顿图。
三,平面图
一、 平面图的定义
在一张纸上画几何模型时常常会发现,不仅允许各边在结点处相交,而且还允许各边在某些非结点处相交,这样的点称为交叉点;而相交的边,称为交叉边。
如果能把一个无向图G的所有结点和边画在平面上,使得任何两边除公共结点外没有其他交叉点,则称G为平面图,否则称G为非平面图。
当且仅当一个图的每个连通分支都是平面图时,这个图是平面图。应当注意,有些图从表面上看它的某些边是相交叉的,但是不能就此肯定它不是平面图。
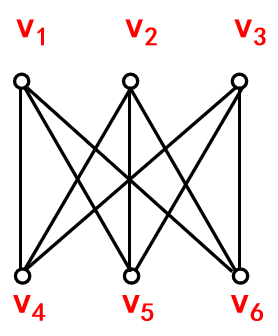
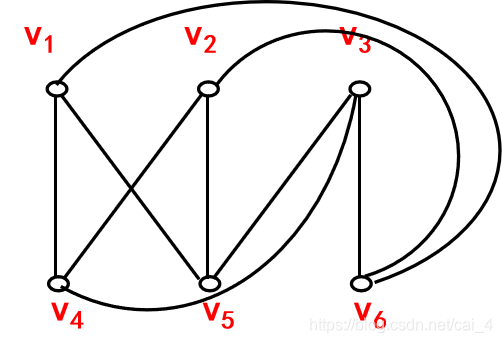
二、非平面图
有些图形不论如何改画,除去结点外,总有边相交叉。
即不管怎样改画,至少有一条边与其他边相交叉,故它是非平面图。
三、 相关概念
定义 在平面图G的一个平面表示中,
由边所包围的其内部不包含图的结点和边的区域,称为G的一个面,
包围该面的诸边所构成的回路称为这个面的边界,
面r的边界的长度称为该面的次数,记为deg®。
区域面积有限的面称为有限面,区域面积无限的面称为无限面。
平面图有且仅有一个无限面。
定理:平面图中所有面的次数之和等于边数的二倍。
证明 因任何一条边,或者是两个面边界的公共边,或者是在一个面中作为边界被重复计算两次,故平面图所有面的次数之和等于其边数的二倍。
四,对偶图与着色
一、对偶图
对于具有n个面的平面图G=<V,E>,实施下列步骤所得到的图G*=<V*,E*>,称为G的对偶图:
(1)在G的每一个面 ri内部作一个G
的顶点vi
V*;
(2)若G的面ri与rj有公共边界ek,那么过边界ek,作关联vi与vj的一条边,且与其他边不相交;
(3)当且仅当ek为ri一个面的边界而非与其他面的公共边界时,作vi
的一条环与ek相交,且仅交于一处,并不与G
的边相交。

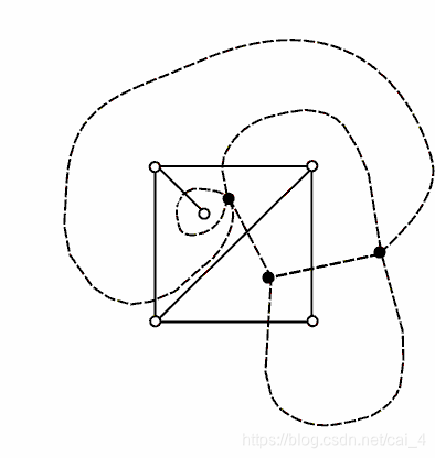
G 的对偶图G
有以下性质:
(1) G
是平面图
(2) 若边e为G中的环,则G
与e对应的边e
为桥,若e为桥,则G
中与e对应的边e
为环.
(3) 同构的平面图的对偶图不一定是同构的.
如上面的例子.
设G
是连通平面图G的对偶图,n
, m*, r
和n, m,
r分别为G
和G的顶点数、边数和面数,则
(1) n*= r
(2) m*=m
(3) r*=n
二、着色
如果用n种颜色给图的所有顶点着色,每个顶点使用一种颜色,使得相邻顶点的颜色不同,那么图称为n-可着色的。对图G着色需要的最少颜色数称为G的着色数,记作x(G)。
Welch Powell给出了对图着色的算法:
输入一个平面图
(1) 按照度的递减顺序排列图中的顶点;
(2)用第一种颜色对第一个顶点着色,并且按排列次序,对与前面着色点不相邻的每一点着上同样的颜色;
(3)用第二种颜色对尚未着色的点重复(2);
(4)用第三种颜色继续这种做法,直至所有点都被着色;