矩阵特征向量和特征值的意义

作者：達聞西

链接：https://www.zhihu.com/question/30094611/answer/120499954

来源：知乎

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

一、先从旋转和缩放角度，理解一下特征向量和特征值的几何意义

从定义来理解特征向量的话，就是经过一个矩阵变换后，空间沿着特征向量的方向上相当于只发生了缩放，比如我们考虑下面的矩阵：

$\begin{bmatrix}1.5 & 0.5\\ 0.5 & 1.0\end{bmatrix}$

求这个变换的特征向量和特征值，分别是：

$U=\begin{bmatrix}0.85 & -0.53\\ 0.53 & 0.85\end{bmatrix}$
（列向量）

和

1.81，0.69

用一个形象的例子来说明一下几何意义，我们考虑下面笑脸图案：

&amp;lt;img src="https://pic4.zhimg.com/02d26c0f63edd30cd75faa3cfb21f47f_b.png" data-rawheight="487" data-rawwidth="562" class="origin_image zh-lightbox-thumb" width="562" data-original="https://pic4.zhimg.com/02d26c0f63edd30cd75faa3cfb21f47f_r.png"&amp;gt;

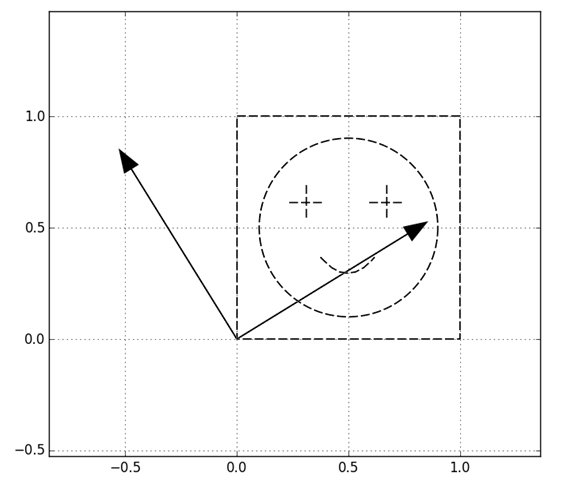
为方便演示笑脸图案在0,0和1,1围起来的单位正方形里，同时也用两个箭头标出来了特征向量的方向。经过
$\begin{bmatrix}1.5 & 0.5\\ 0.5 & 1.0\end{bmatrix}$
的变换，也就是用这个图案中的每个点的坐标和这个矩阵做乘法，得到下面图案：

&amp;lt;img src="https://pic1.zhimg.com/8f00cbd08d019eed528e2f3202034c3c_b.png" data-rawheight="325" data-rawwidth="556" class="origin_image zh-lightbox-thumb" width="556" data-original="https://pic1.zhimg.com/8f00cbd08d019eed528e2f3202034c3c_r.png"&amp;gt;可以看到就是沿着两个正交的，特征向量的方向进行了缩放。这就是特征向量的一般的几何理解，这个理解我们也可以分解一下，从旋转和沿轴缩放的角度理解，分成三步：

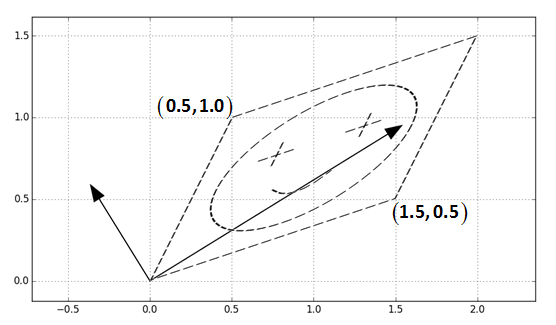
可以看到就是沿着两个正交的，特征向量的方向进行了缩放。这就是特征向量的一般的几何理解，这个理解我们也可以分解一下，从旋转和沿轴缩放的角度理解，分成三步：

第一步

，把特征向量所指的方向分别转到横轴和纵轴

&amp;lt;img src="https://pic4.zhimg.com/8ca691941f4b219f58696e329776d933_b.png" data-rawheight="506" data-rawwidth="1370" class="origin_image zh-lightbox-thumb" width="1370" data-original="https://pic4.zhimg.com/8ca691941f4b219f58696e329776d933_r.png"&amp;gt;

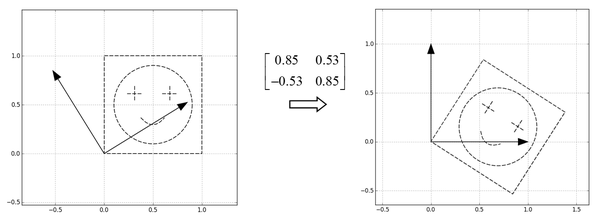
这一步相当于用U的转置，也就是
$U^{T}$
进行了变换

第二步

，然后把特征值作为缩放倍数，构造一个缩放矩阵
$\begin{bmatrix}1.81 & 0\\ 0 & 0.69\end{bmatrix}$
，矩阵分别沿着横轴和纵轴进行缩放：

&amp;lt;img src="https://pic2.zhimg.com/df8b17255468437169b3f9d598cae81d_b.png" data-rawheight="428" data-rawwidth="1147" class="origin_image zh-lightbox-thumb" width="1147" data-original="https://pic2.zhimg.com/df8b17255468437169b3f9d598cae81d_r.png"&amp;gt;

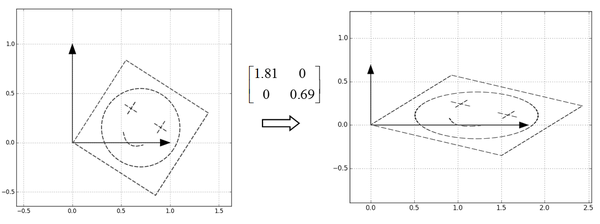
第三步

，很自然地，接下来只要把这个图案转回去，也就是直接乘U就可以了

&amp;lt;img src="https://pic3.zhimg.com/7f9259783e516732e1c1009829c4e6f2_b.png" data-rawheight="369" data-rawwidth="1126" class="origin_image zh-lightbox-thumb" width="1126" data-original="https://pic3.zhimg.com/7f9259783e516732e1c1009829c4e6f2_r.png"&amp;gt;所以，从旋转和缩放的角度，一个矩阵变换就是，旋转–&amp;amp;gt;沿坐标轴缩放–&amp;amp;gt;转回来，的三步操作，表达如下：

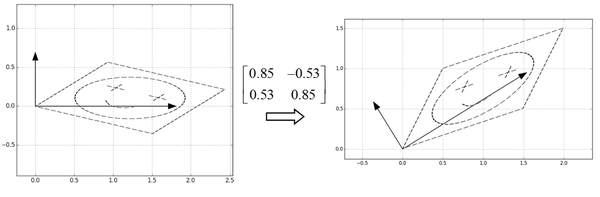
所以，从旋转和缩放的角度，一个矩阵变换就是，旋转–>沿坐标轴缩放–>转回来，的三步操作，表达如下：

$T=U \Sigma U ^{T}$

多提一句，这里给的是个(半)正定矩阵的例子，对于不镇定的矩阵，也是能分解为，旋转–>沿坐标轴缩放–>旋转，的三步的，只不过最后一步和第一步的两个旋转不是转回去的关系了，表达如下：

$T=U \Sigma V^{T}$

这个就是SVD分解，就不详细说了。

另外，这个例子是二维的，高维类似，但是形象理解需要脑补。

二、协方差矩阵的特征向量

PCA的意义其他答主都说得差不多了，一句话概括就是找到方差在该方向上投影最大的那些方向，比如下边这个图是用
$\begin{bmatrix}1 & 0.5\\ 0.5 & 1\end{bmatrix}$
作为些协方差矩阵产生的高斯分布样本：

：

&amp;lt;img src="https://pic2.zhimg.com/06774664010719ea169deb44ba6240fd_b.png" data-rawheight="409" data-rawwidth="671" class="origin_image zh-lightbox-thumb" width="671" data-original="https://pic2.zhimg.com/06774664010719ea169deb44ba6240fd_r.png"&amp;gt;大致用个椭圆圈出来分布，相关性最强的（0.707，0.707）方向就是投影之后方差最大的方向。

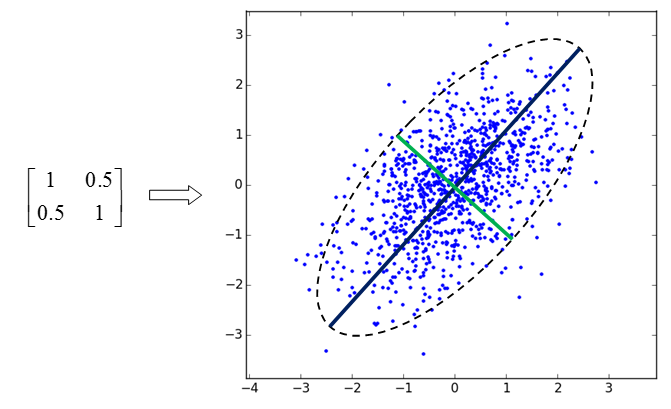
大致用个椭圆圈出来分布，相关性最强的（0.707，0.707）方向就是投影之后方差最大的方向。

接下来我们不尝试严格证明，而是从旋转和缩放的角度形象理解一下，我们可以考虑把这个分布也旋转一下，让长轴在x轴上，短轴在y轴上，变成如下：

&amp;lt;img src="https://pic1.zhimg.com/36ed9b9b895003148e75ffaa7bfad708_b.png" data-rawheight="345" data-rawwidth="544" class="origin_image zh-lightbox-thumb" width="544" data-original="https://pic1.zhimg.com/36ed9b9b895003148e75ffaa7bfad708_r.png"&amp;gt;然后再沿着x轴和y轴，除以标准差，缩放成标准差为1的单位分布

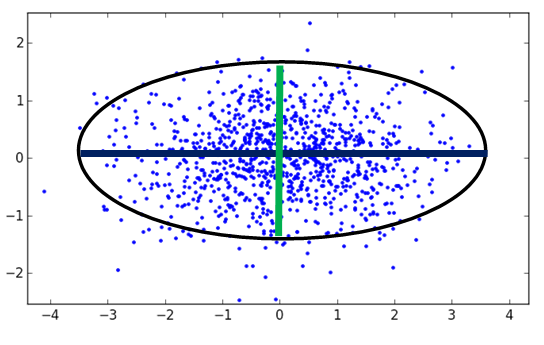
然后再沿着x轴和y轴，除以标准差，缩放成标准差为1的单位分布

&amp;lt;img src="https://pic3.zhimg.com/327ec561707f4efd51c178b4c1eb0af2_b.png" data-rawheight="461" data-rawwidth="481" class="origin_image zh-lightbox-thumb" width="481" data-original="https://pic3.zhimg.com/327ec561707f4efd51c178b4c1eb0af2_r.png"&amp;gt;注意，在这个除以标准差的过程中，标准差最大的轴，就对应着原空间中，样本投影后方差最大的方向。接下来，假设这个分布中的样本为

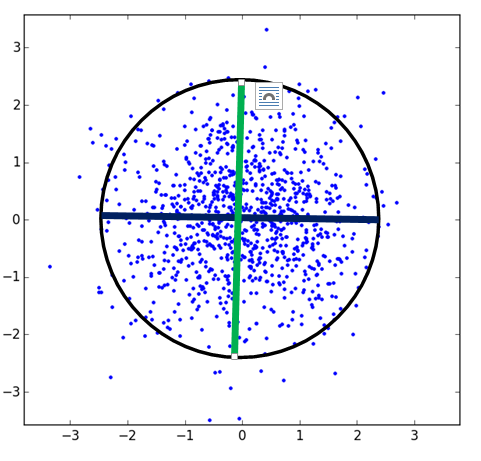
注意，在这个除以标准差的过程中，标准差最大的轴，就对应着原空间中，样本投影后方差最大的方向。接下来，假设这个分布中的样本为
$X_U$
，则我们可以把一开始的样本表示为：

$X=ULX_U$

用这么别扭的表示方式主要是为了接下来推公式方便，所以接下来推个简单的公式：

协方差矩阵，用S表示，则有

$S_{ij}=E\left[ (X_i-\mu _i)(X_j-\mu _j) \right]$

因为这个分布里两个维度的均值都是0，所以有

$S_{ij}=E\left[ X_iX_j \right]$

所以

$S=\frac{1}{N} XX^T$

其中N是样本数，根据前面的
$X=ULX_U$
，进一步展开这个公式：

$S=\frac{1}{N} XX^T=\frac{1}{N}(ULX_U)(ULX_U)^T=UL(\frac{1}{N}X_U{X_U}^T)L^TU^T$

因为
$X_U$
是个单位方差的且无相关性的样本，所以
$\frac{1}{N}X_U{X_U}^T=I$

另外L是个对角矩阵所以有

$S=ULL^TU^T=UL^2U^T=U\Sigma U^T$