系列文章目录
第六章:狄克斯特拉算法
前言
积累算法,记录学习
一、加权图
上一章介绍的图是没有权重的,即每一条边的意义一样,这样并不全面,因此引出一种加权图,这种图通常伴随的问题是
最快路径问题
比如对应下面这个图,假如使用广度优先算法时,找到的最短路径可能是“起点——A——终点”或者“起点——B——终点”,但是我们可以看出,在图上最快的路径并不是上述两条!因此广度优先搜索算法失效。对于这样的加权图,我们的狄克斯特拉算法就派上了用场。

二、算法原理
我们不用那种索然无味的算法流程,我们还是以上图为例,我们的目的是找到从起点到终点的最快路径,我们分以下步骤进行:
1)
找出最近的节点。
我们从起点出发,有两条路能走,前往A点和前往B点,最终目的是终点。并且我们可以知道前往A点用6分钟,前往B点用2分钟,不知道前往终点所需时间,因此设为无穷。所以来说,我们选择B节点这条路,因为它是最快的!拿小本子记下来:
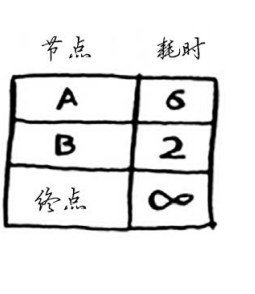
2)
计算经B节点前往其各个邻居的所需时间。
现在我们站在B处,能够到达的地方有A和终点,所以从B到A的时间是3分钟,从B到终点的时间是5分钟。由此我们需要更新一下自己的小本子了。因为现在从起点到A点的最快时间是5分钟,到终点的最快时间是7分钟:
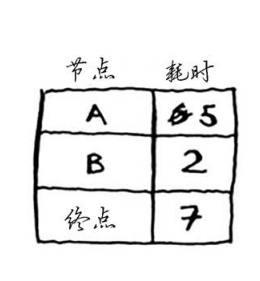
3)重复!我们现在再站在A点,由于A点到终点的时间是1分钟,因此又要更新一下小本子,因为现在从起点途径B再途径A再到终点才是我们的最快路径!仅需6分钟,显然这不是我们最短路径。

这些路上的时间在权重图的术语中叫
权重
这里需要注意一点,狄克斯特拉算法不能用在包含带有负权重的图中,因为对于处理过的节点,算法认为没有前往该节点的更短路径,这时我们就需要一种新的算法——
贝尔曼-福德算法
,这里暂时先不做详解,感兴趣的小伙伴可以自行学习。
三、算法实现
我们就实现上面这个图的狄克斯特拉算法,使用的数据结构也是散列表:它真是用处多多呢!
1、首先我们需要有存储图的散列表graph,将图上所有的信息表现在散列表中,这就是我们第一步要做的事:
>>> graph = {}
>>> graph["start"] = {}
>>> graph["start"]["a"] = 6
>>> graph["start"]["b"] = 2
>>> graph["a"] = {}
>>> graph["a"]["end"] = 1
>>> graph["b"] = {}
>>> graph["b"]["a"] = 3
>>> graph["b"]["end"] = 5
>>> graph["end"] = {}
>>> graph
{'start': {'a': 6, 'b': 2}, 'a': {'end': 1}, 'b': {'a': 3, 'end': 5}, 'end': {}}
2、然后有需要记录花费时间的散列表costs,这个是要更新的,所以我们先给他一个初始状态就行,就是站在起点我们所获知的时间花费,无穷用
infinity = float("inf")
表示
>>> infinity = float("inf")
>>> costs = {}
>>> costs["a"] = 6
>>> costs["b"] = 2
>>> costs["end"] = infinity
>>> costs
{'a': 6, 'b': 2, 'end': inf}
3、因为要记住路径,我们也就需要散列表来记住父节点,用parents来表示,当我们在起点时,a的父节点是起点,b的父节点也是起点,前往终点的父节点暂时未知为None。
>>> parents = {}
>>> parents["a"] = "start"
>>> parents["b"] = "start"
>>> parents["end"] = None
4、为了避免有双向图的可能性,我们需要记录一下处理过的点,避免陷入循环,所以要设置一个
processed = []
下面编写寻找最近邻居的程序:
def find_lowest_cost_node(costs):
lowest_cost = float("inf")
lowest_cost_node = None
for node in costs:
cost = costs[node]
if cost < lowest_cost and node not in processed:
lowest_cost = cost
lowest_cost_node = node
return lowest_cost_node
狄克斯特拉算法:
def dkstl(costs):
fastest_path = []
node = find_lowest_cost_node(costs)
fastest_path.append(node)
while node is not None:
cost = costs[node]
neighbors = graph[node]
for n in neighbors.keys():
new_cost = cost + neighbors[n]
if costs[n] > new_cost:
costs[n] = new_cost
parents[n] = node
processed.append(node)
node = find_lowest_cost_node(costs)
fastest_path.append(node)
return fastest_path
运行结果:

四、总结
- 广度优先搜索用于在非加权图中查找最短路径。
- 狄克斯特拉算法用于在加权图中查找最短路径。
- 仅当权重为正时狄克斯特拉算法才管用。
- 如果图中包含负权边,请使用贝尔曼–福德算法。