转载于:https://blog.csdn.net/reborn_lee/article/details/81139195
序言
这里讲的离散时间傅里叶变换(DTFT)是针对离散非周期信号的DTFT,事实上,DTFT本身也就是为了表示非周期信号而出现的。
推导的过程采用与连续时间傅里叶变换完全并行的思路,连续时间傅里叶变换的推导参看博文:
连续时间信号的傅里叶变换
对连续时间傅里叶变换的一点回顾:
在
连续时间傅里叶变换
这篇博文中,我们看到,一个连续时间周期方波的傅里叶级数可以看成一个包络函数的采样值,并且随着这个方波周期的增大,这些样本越来越密。这一性质就让人想到一个非周期信号
x(
t
)
x(t)
x
(
t
)
可以这样来表示,即首先产生一个周期信号
x(
t
)
~
\tilde{x(t)}
x
(
t
)
~
,使
x(
t
)
~
\tilde{x(t)}
x
(
t
)
~
在一个周期内等于
x(
t
)
x(t)
x
(
t
)
,然后随着这个周期无限大,
x(
t
)
~
\tilde{x(t)}
x
(
t
)
~
就会在一个越来越大的时间间隔上等于
x(
t
)
x(t)
x
(
t
)
,这样对
x(
t
)
~
\tilde{x(t)}
x
(
t
)
~
的傅里叶级数表示也就收敛于
x(
t
)
x(t)
x
(
t
)
的傅里叶变换表示。
采用与连续时间傅里叶变换完全并行的思路推理




综合公式:

分析公式:
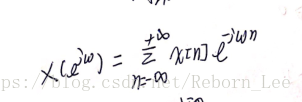
在推导这些公式的过程中,可以看出一个非周期序列是怎样被看成复指数信号的线性组合的。事实上,综合公式:

本身就是把序列
x
[
n
]
x[n]
x
[
n
]
作为一种复指数序列的线性组合来表示的,这些复指数序列在频率上是无限靠近的,其幅度为
X
(
e
j
w
)
X(e^{jw})
X
(
e
j
w
)
往往称为
x
[
n
]
x[n]
x
[
n
]
的频谱,因为它给出这样的信息:
x
[
n
]
x[n]
x
[
n
]
是怎样由这些不同频率的复指数序列组成的。
值得提及的是,与连续时间情况一样,上述离散时间傅里叶变换的推导过程给我们在离散时间傅里叶级数和离散时间傅里叶变换之间提供了一种重要的关系。
特别是一个周期序列
x
[
n
]
~
\tilde{x[n]}
x
[
n
]
~
的傅里叶系数
a
k
a_{k}
a
k
可以用一个有限长序列
x
[
n
]
x[n]
x
[
n
]
的傅里叶变换的等间隔样本来表示
,这个
x
[
n
]
x[n]
x
[
n
]
就等于一个周期上的
x
[
n
]
~
\tilde{x[n]}
x
[
n
]
~
,而在其余地方为0。

一句重要的废话(理解):
下面这句话,在看完这个系列的博文后就能懂得。
正如推导过程中表明的,离散时间傅里叶变换和连续时间傅里叶变换相比有很多相似之处。两者的主要差别在于
①离散时间傅里叶变换
X(
e
j
w
)
X(e^{jw})
X
(
e
j
w
)
的周期性和②在综合公式中的有限积分区间。
这两者来自这样的一个事实:在频率上相差
2π
2\pi
2
π
的离散时间复指数信号是完全一样的。(参考博文:
离散时间复指数序列的周期性质
)。由
离散时间周期信号的傅里叶级数
这篇博文,可知,对周期离散时间序列而言,这就意味着傅里叶级数系数也是周期的,并且
傅里叶级数表示是一个有限项的和式
。对非周期信号而言,
这就意味着
X(
e
j
w
)
X(e^{jw})
X
(
e
j
w
)
也是周期的,周期为
2π
2\pi
2
π
,并且综合公式只涉及一个频率区间内的积分,这个频率区间就是产生不同复指数信号的那个间隔,即任何
2π
2\pi
2
π
长度的间隔。
最后再次来一个重磅的结论:
ej
w
n
e^{jwn}
e
j
w
n
作为
ww
w
的函数的周期性的进一步的结果是:
w=
0
w=0
w
=
0
和
w=
2
π
w=2 \pi
w
=
2
π
都得到同一个信号。因此,位于
这些频率值或者任何
π\pi
π
偶数倍的
ww
w
附近都是慢变化的
,从而都对应
低频率
的信号;而
靠近
π\pi
π
的奇数倍的
ww
w
,在离散情况下都相应于
高的频率
。如下图:

注:下面的这些结论不看也罢,我只是觉得有意思才贴出来的。