卡尔曼滤波
使用卡尔曼滤波做了一些东西以后,其实还有很多理论的东西,都没有深入的理解,只是简单的使用,先对卡尔曼滤波做一个简单的总结,后续,如果有更深入的理解,再做补充。
-
一步预测

以上就是离散型卡尔曼滤波基本方程。只需要给定初始值
X
^
0
\hat{X}_0
X
^
0
和
P
0
P_0
P
0
,根据
k
k
k
时刻的测量值
z
k
z_k
z
k
就可以得到递推计算得到
k
k
k
时刻的状态。
算法可用下图表示。可以看到有滤波计算回路和增益计算回路。
增益计算回路独立于滤波计算回路,而滤波计算回路依赖于增益计算回路。
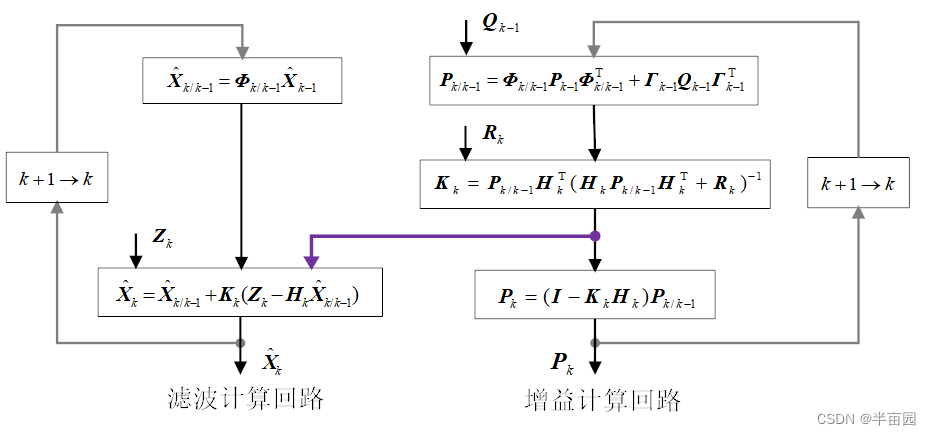
卡尔曼滤波具有两个明显的信息更新过程:时间更新过程和测量更新过程。第一个公式:根据
k
−
1
k-1
k
−
1
时刻的状态估计
预测
k
k
k
时刻的状态估计方法。第二个公式是对这种
预测的质量优劣
做了定量的计算。这两个公式的计算仅使用了
与系统的动态特性有关的信息
,如一步转移阵,噪声驱动阵,驱动噪声的方差阵。从时间推移的角度看,这两个公式将时间从
k
−
1
k-1
k
−
1
推到了
k
k
k
时刻。这两个公式也描述了卡尔曼滤波的时间更新过程。
剩下的式子,用来计算对事件更新值的
修正量
。该修正量由时间更新的质量的优劣
P
k
/
k
−
1
P_{k/k-1}
P
k
/
k
−
1
,测量信息的质量优劣
R
k
R_k
R
k
,量测与状态的关系
H
k
H_k
H
k
,测量值
Z
k
Z_k
Z
k
。所有这些方程围绕一个目的,合理正确的利用测量值
Z
k
Z_k
Z
k
。
-
推导过程
增益阵和估计均方误差阵推导
增益阵选取的规则:使估计的均方误差
Pk
=
E
[
X
k
~
X
k
~
T
]
P_k = E[\tilde{X_k}\tilde{X_k}^{\Tau}]
P
k
=
E
[
X
k
~
X
k
~
T
]
达到最小。
关于公式的推导,我也不知道怎么说,反正我是推一次忘一次,不过公式确实是不会变的,不推也不是不能用,只要弄清楚每个变量的含义就可以了。如果想要深入的理解,可以参考第三本书。
关于算法的理解,可以看看第一个网页,适合入门理解。
关于算法的实现,可以看黄小平的《卡尔曼滤波原理及应用》,例子比较多,在实例中体会每个公式的用法,会理解的比较快。
参考文献:
http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/
http://www.psins.org.cn/
卡尔曼滤波与组合导航原理第三版
卡尔曼滤波原理及应用