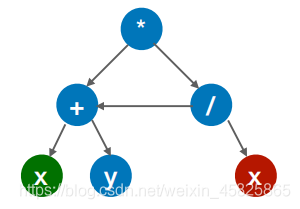
有向无环图(DAG图)
一.基础知识
有向无环图:有向图+无环
简称:Directed Acyclic Graph(DAG图)
directed 径直的 [dəˈrektɪd]
acyclic 无环的 [ˌeɪˈsaɪklɪk]
graph 图 [ɡræf]
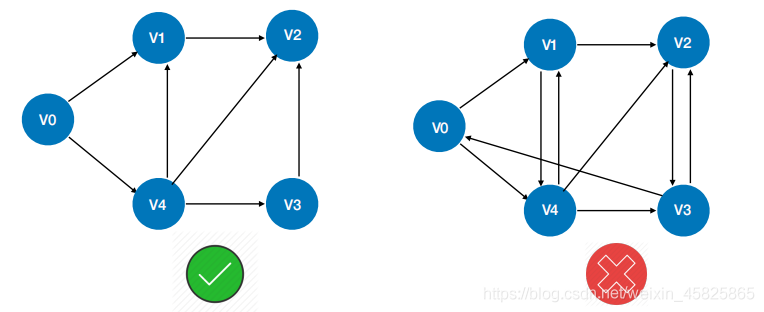
二.化简
找到重复部分
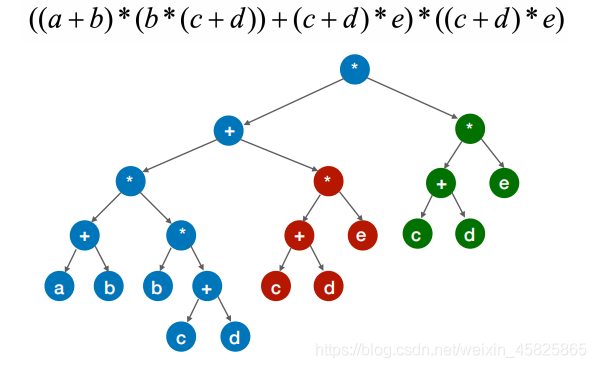
修改
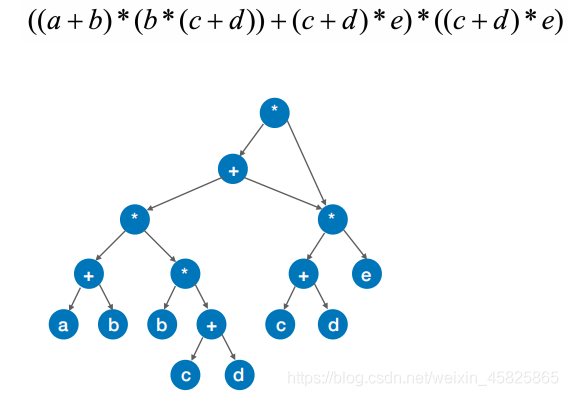
再找
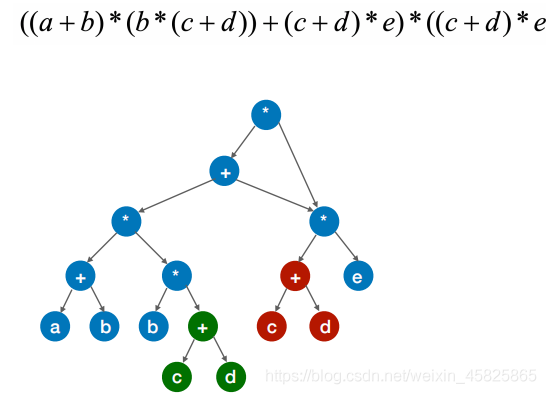
再改
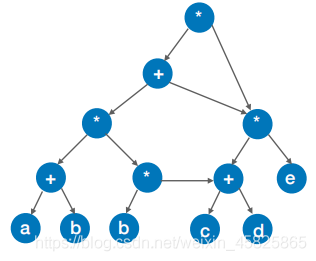
再找
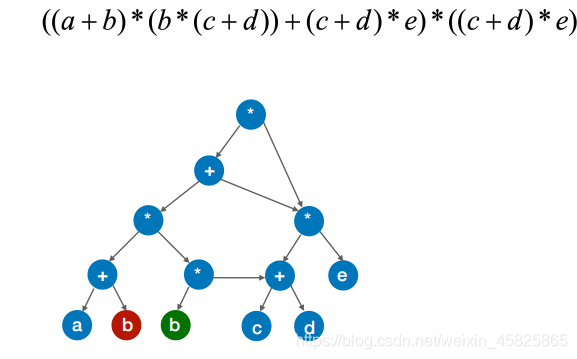
再改
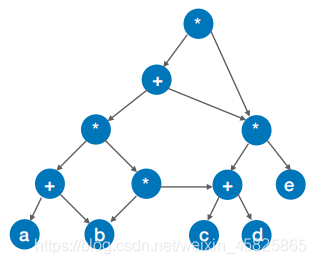
完成
三.构建
为防止化简遗漏,通常需要自己构建
((a+b)* b*(c+d))+(c+d)* e)*((c+d)*e)
1.构建底层

2.按照运算符计算顺序依次构建
题目:{ (a+b)* [b*(c+d)] + (c+d)* e} * [(c+d)*e]
a+b
c+d
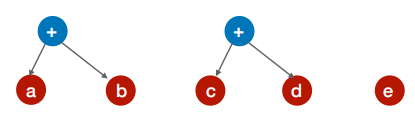
[b*(c+d)] 注意分层
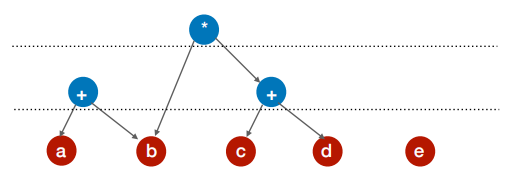
题目:{ (a+b)* [b*(c+d)] + (c+d)* e} * [(c+d)*e]
(a+b)* [b*(c+d)]
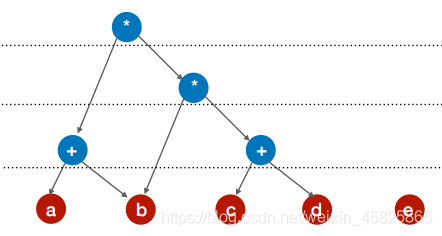
题目:{ (a+b)* [b*(c+d)] + (c+d)* e} * [(c+d)*e]
(c+d)* e
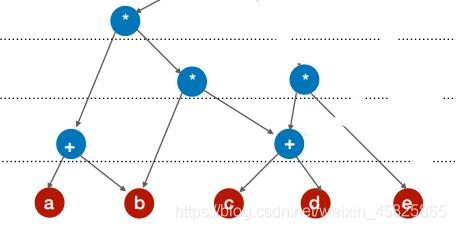
题目:{ (a+b)* [b*(c+d)] + (c+d)* e} * [(c+d)*e]
{ (a+b)* [b*(c+d)] + (c+d)* e}
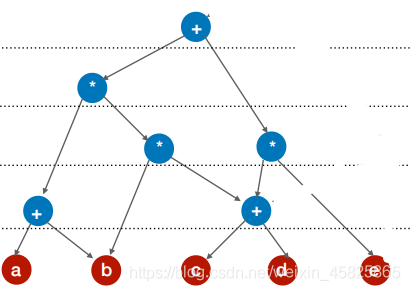
题目:{ (a+b)* [b*(c+d)] + (c+d)* e} * [(c+d)*e]
(c+d)* e 已算过
{ (a+b)* [b*(c+d)] + (c+d)* e} * [(c+d)*e]
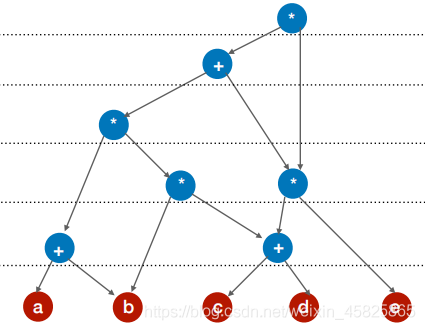
通常正确构建,检查时无需修改,本题即是
3.检查。自底向上依次检查同层是否出现重复,若有修改
举例:
绿色部分,都是c+d去乘某个数
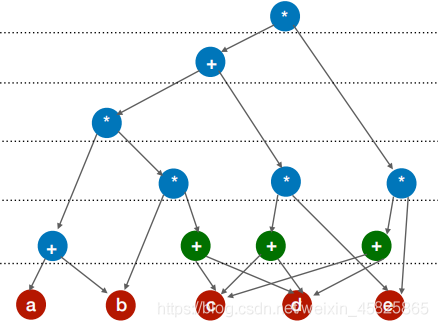
修改为
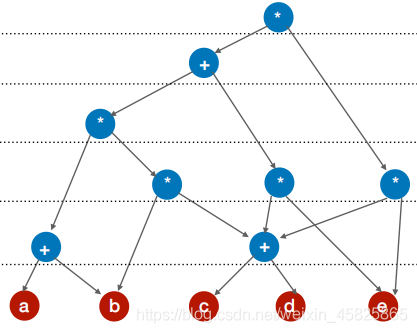
再如:
出现两个(c+d) * e
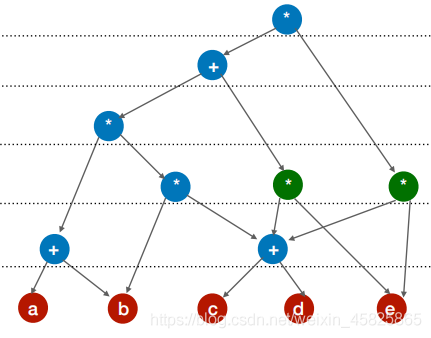
修改为:
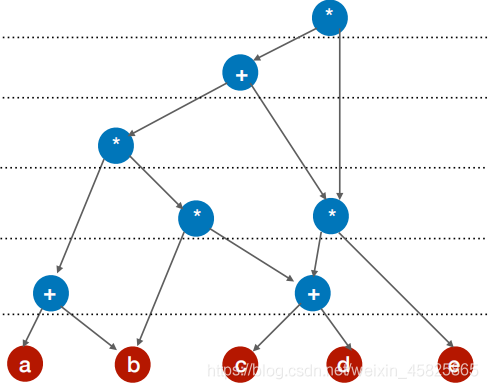
四.进阶
( a * b ) * ( a * b ) * ( a * b ) * c
分步构建
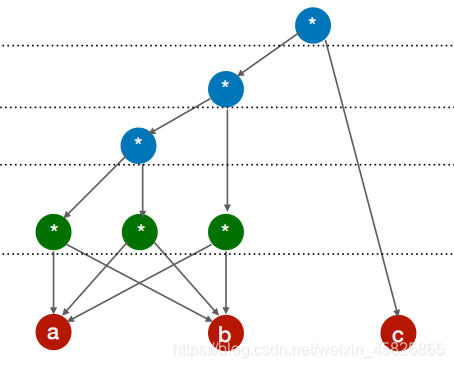
检查删掉重复部分:同层3个a*b,保留一个(此处保留了中间的)
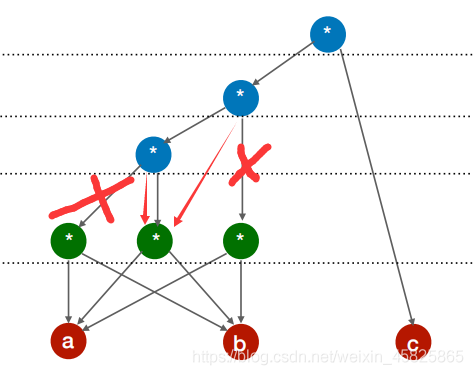
即:(通过练习可一步到位)
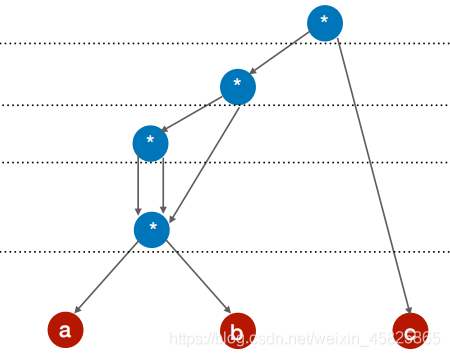
注:( a * b ) * ( a * b ) * ( a * b ) * c
刚刚我们是按照从左到后的顺序构建的,如果改变构建顺序,如:先计算 ( a * b ) * c会导致图不一样,因此考试中可能不会对此过深考察
五.练习

解:
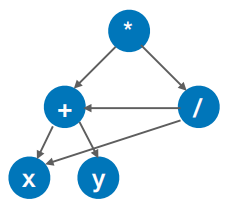
答案:A
提醒:不要忘了x也可以合并,我们在构建过程中底层的每个顶点是只出现一次的