QR分解法
QR分解法,将原矩阵
A
m
×
n
A_{m\times n}
Am×n分解成一个正交矩阵
Q
m
×
n
Q_{m\times n}
Qm×n(
Q
T
Q
=
I
Q^{T}Q = I
QTQ=I)和一个上三角矩阵
R
n
×
n
R_{n\times n}
Rn×n(对角线下面的元素全为0)的乘积。QR分解主要有三种方法:Gram-Schmid正交化法、Household变换法、Givens变换法。
1 Gram-Schmid正交化法
这种方法主要利用了斯密特正交化方法,该方法还可以通过单位正交化来构建向量空间的标准正交基。
1.1 单位正交化
已知在
n
n
n维空间中的任意位置都可以由该空间的
n
n
n个单位正交向量表示。这
n
n
n个单位正交向量构成了该
n
n
n维空间的基,即单位正交基(标准正交基)。
标准正交基的特点: 单位正交基是由单位向量构造成,,即每个向量的模长都为单位长度1,并且不同向量之间两两正交,即内积为0。
单位正交化的步骤
已知
α
1
,
α
2
,
…
,
α
n
\alpha _1,\alpha _2,\dots,\alpha _n
α1,α2,…,αn是
n
n
n个线性无关向量,如何将这
n
n
n个向量构成标准正交基(即单位正交化)?
- 施密特正交化
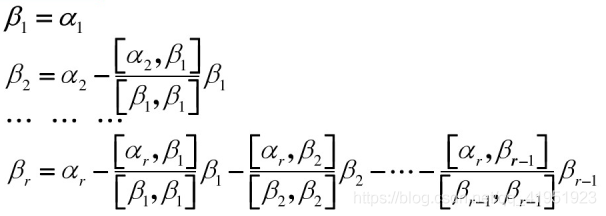 则
则
β
1
,
β
2
,
…
,
β
n
\beta _1,\beta _2,\dots,\beta _n
β1,β2,…,βn两两正交,并且[
β
1
,
β
2
,
…
,
β
n
]
[\beta _1,\beta _2,\dots,\beta _n]
[β1,β2,…,βn]与[
α
1
,
α
2
,
…
,
α
n
]
[\alpha _1,\alpha _2,\dots,\alpha _n]
[α1,α2,…,αn]等价。 - 单位化
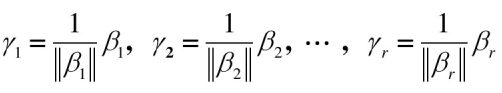
则可得与[
α
1
,
α
2
,
…
,
α
n
]
[\alpha _1,\alpha _2,\dots,\alpha _n]
[α1,α2,…,αn]等价的单位正交基[
γ
1
,
γ
2
,
…
,
γ
n
]
[\gamma _1,\gamma _2,\dots,\gamma _n]
[γ1,γ2,…,γn]。
1.2 QR分解求特征值过程
栗子
求矩阵
A
A
A的
Q
R
QR
QR分解
A
=
[
1
2
2
1
0
2
0
1
1
]
A = \begin{bmatrix} 1&2&2\\ 1&0&2\\ 0&1&1\\ \end{bmatrix}
A=⎣⎡110201221⎦⎤
解:
- 已知
A
A
A的列向量为:
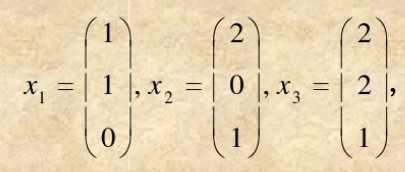
A
A
A的三个列向量无线性关系,因此A
A
A为满秩矩阵,可以进行Q
R
QR
QR分解。 - 使用斯密特正交化方法将
x
1
,
x
2
,
x
3
x_1,x_2,x_3
x1,x2,x3正交化:
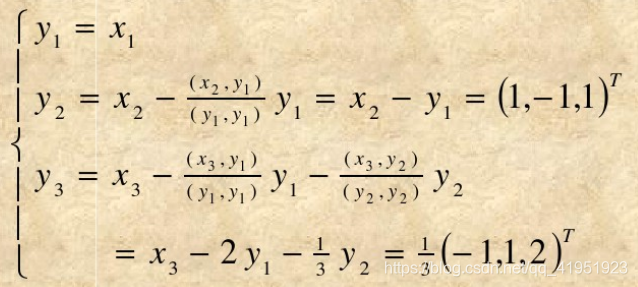
- 单位化:
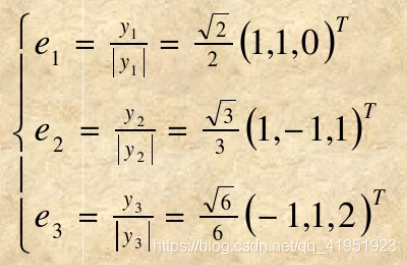
- 整理:
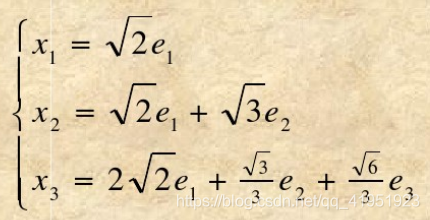
- 求的
Q
Q
Q和R
R
R:
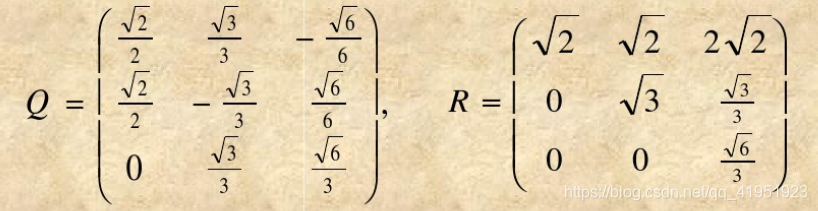
A
=
Q
R
A = QR
A=QR
2 利用Householder变换进行QR分解
2.1 Householder变换
Householder变换又称为反射变换或镜像变换。在
R
3
R^3
R3中,给定一个向量
α
\alpha
α,令
β
\beta
β表示
α
\alpha
α关于平面
π
\pi
π(以
ω
\omega
ω为法向量)的反射变换所得像
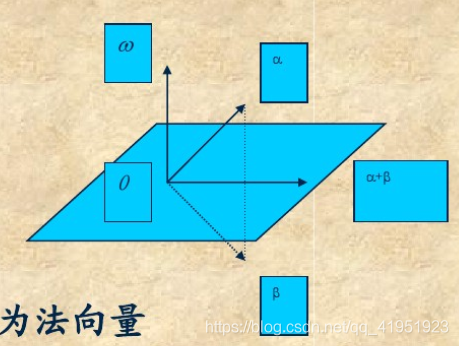
记
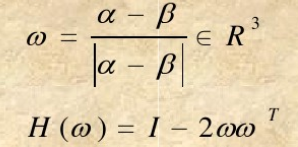
则
![]()
该变换将向量
α
\alpha
α变成了以
ω
\omega
ω为法向量的平面的对称向量。
定义 设
ω
∈
C
n
\omega \in C^n
ω∈Cn是一个单位向量,令
H
(
ω
)
=
I
−
2
ω
ω
H
H(\omega) = I – 2\omega \omega ^H
H(ω)=I−2ωωH称
H
H
H为一个Householder矩阵。
Householder矩阵的性质
设
H
H
H是一个Householder矩阵,则
-
H
H
H是Hermite矩阵,H
H
=
H
H^H = H
HH=H; -
H
H
H是酉矩阵,H
H
H
=
I
H^H H = I
HHH=I; -
H
H
H是对合矩阵,H
2
=
I
H^2 = I
H2=I; -
H
H
H是自逆矩阵,H
−
1
=
H
H^{-1} = H
H−1=H; -
d
i
a
g
(
I
,
H
)
diag(I,H)
diag(I,H)也是一个Householder矩阵; -
d
e
t
(
H
)
=
−
1
det(H) = -1
det(H)=−1。
定理 设
u
∈
C
n
u \in C^n
u∈Cn是一个单位向量,则对于任意
x
∈
C
n
x \in C^n
x∈Cn,存在Householder矩阵
H
H
H,使得
H
x
=
a
u
Hx = au
Hx=au,其中
∣
a
∣
=
∣
∣
x
∣
∣
2
|a| = ||x||_2
∣a∣=∣∣x∣∣2,
a
x
H
u
ax^Hu
axHu为实数。
推论1 对于任意的
x
∈
C
n
x \in C^n
x∈Cn,存在Householder矩阵
H
H
H,使得
H
x
=
a
e
1
Hx = ae_1
Hx=ae1,其中
∣
a
∣
=
∣
∣
x
∣
∣
2
|a| = ||x||_2
∣a∣=∣∣x∣∣2,
a
x
H
e
1
ax^He_1
axHe1为实数。
推论2 对于任意的
x
∈
C
n
x \in C^n
x∈Cn,存在Householder矩阵
H
=
I
−
2
u
u
T
H = I – 2uu^T
H=I−2uuT,(
u
∈
R
n
,
u
T
u
=
1
u \in R^n , u^Tu=1
u∈Rn,uTu=1),使得
H
x
=
a
e
1
Hx = ae_1
Hx=ae1,其中
∣
a
∣
=
∣
∣
x
∣
∣
2
|a| = ||x||_2
∣a∣=∣∣x∣∣2
上述结论表明,可以利用Householder变换将任意向量
x
∈
R
n
x \in R^n
x∈Rn化为与第一自然基向量
e
1
e_1
e1平行的向量(共线)。
2.2 利用Householder矩阵求矩阵的QR分解的步骤
-
将矩阵
A
A
A按列分块
A
=
(
α
1
,
α
2
,
…
,
α
n
)
A = (\alpha _1,\alpha _2,\dots,\alpha _n)
A=(α1,α2,…,αn),取
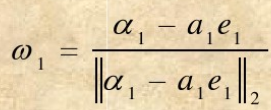
其中
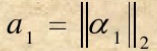
则
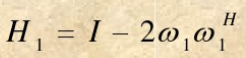
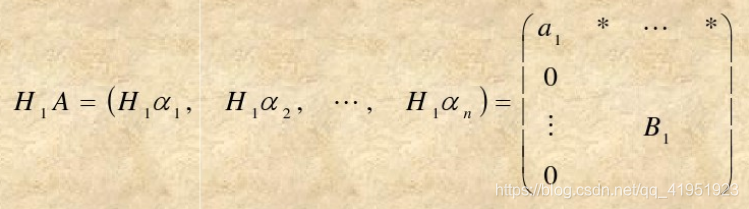
-
将矩阵
B
1
∈
C
(
n
−
1
)
×
(
n
−
1
)
B_1 \in C^{(n-1)\times(n-1)}
B1∈C(n−1)×(n−1)按列分块,
B
1
=
(
β
1
,
β
2
,
…
,
β
n
)
B_1 = (\beta_1,\beta_2,\dots,\beta_n)
B1=(β1,β2,…,βn)取
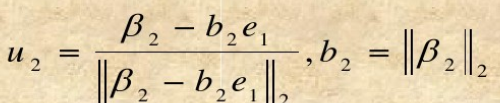
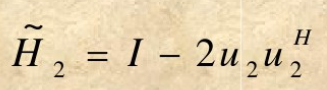
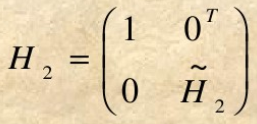
则
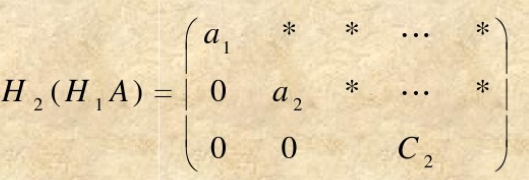
其中
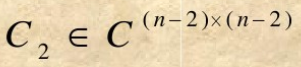
依次进行下去,得到第n
−
1
n-1
n−1个
n
n
n阶的Householder矩阵
H
n
−
1
H_{n-1}
Hn−1,使得
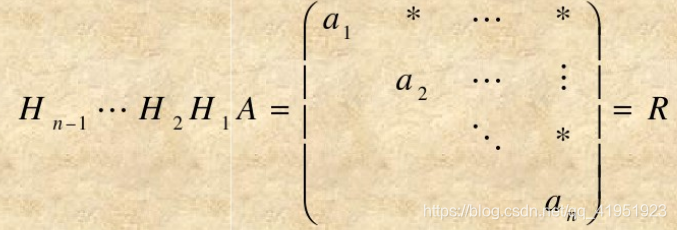
-
因为
H
i
H_i
Hi为自逆矩阵,令
Q
=
H
1
H
2
…
H
n
−
1
Q = H_1 H_2 \dots H_{n-1}
Q=H1H2…Hn−1
则A
=
Q
R
A = QR
A=QR
栗子
已知矩阵
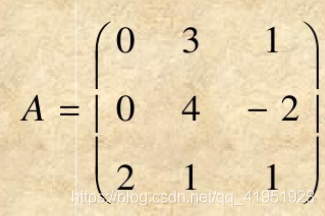
利用Householder变换求
A
A
A的
Q
R
QR
QR分解。
解
因为

令
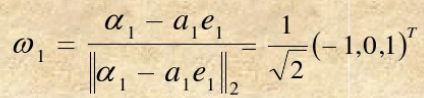
则
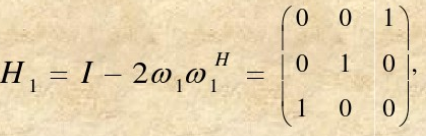 计算
计算
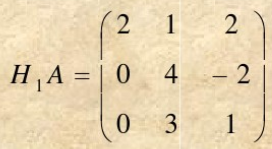
记
β
2
\beta_2
β2等于
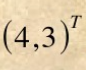
则
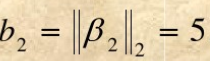
令
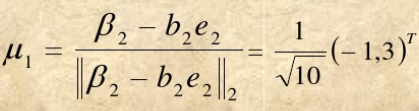
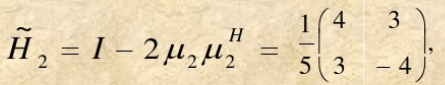
记
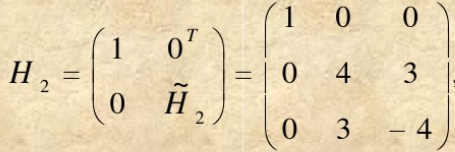
则
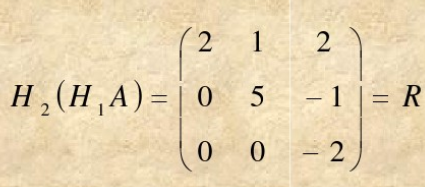
取
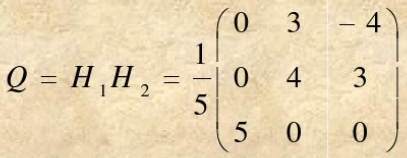
则
A
=
Q
R
A = QR
A=QR
3 利用Givens变换进行QR分解
3.1 Givens变换
在平面坐标
R
2
R^2
R2中向量的旋转变换关系可由旋转角
θ
\theta
θ表示。
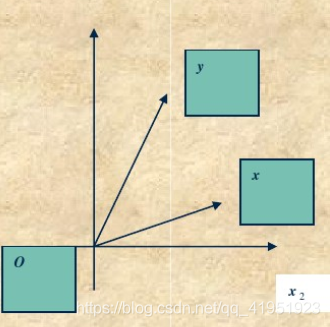 其中
其中
T
T
T是正交矩阵,称为平面旋转矩阵。将其推广到一般的
n
n
n维酉空间中,可以得到初等旋转变换,称为Givens变换。
定义 设
c
,
s
∈
C
n
c,s \in C^n
c,s∈Cn,
∣
c
∣
2
+
∣
s
∣
2
=
1
|c|^2 + |s|^2 = 1
∣c∣2+∣s∣2=1,则记
n
n
n阶矩阵

称
T
k
l
T_{kl}
Tkl为Givens矩阵或初等旋转矩阵。
由
T
k
l
T_{kl}
Tkl所确定的线性变换称为Givens变换或初等旋转变换。Givens矩阵为酉矩阵,且
d
e
t
T
k
l
=
1
det T_{kl} = 1
detTkl=1。
定理 由于任意向量
x
∈
C
n
x \in C^n
x∈Cn,存在Givens变换
T
k
l
T_{kl}
Tkl,使得
T
k
l
x
T_{kl}x
Tklx的第
1
1
1个分量为0,第
k
k
k个分量为非负实数,其余分量不变。
推论给定一个向量
x
∈
C
n
x\in C^n
x∈Cn,则存在一组Givens矩阵
T
12
,
T
13
,
…
,
T
1
n
T_{12},T_{13},\dots,T_{1n}
T12,T13,…,T1n,使得
T
12
T
13
…
T
1
n
x
=
∣
∣
x
∣
∣
2
e
1
T_{12}T_{13}\dots T_{1n}x = ||x||_2 e_1
T12T13…T1nx=∣∣x∣∣2e1,因此通过Givens变换将向量
x
∈
C
n
x\in C^n
x∈Cn与第一自然基向量
e
1
e_1
e1共线。
3.2 利用Givens矩阵求矩阵的QR分解的步骤
- 先将矩阵
A
A
A按列分块,A
=
(
α
1
,
α
2
.
…
,
α
n
)
,
A
∈
C
n
×
n
A = (\alpha_1,\alpha_2.\dots,\alpha_n),A\in C^{n\times n}
A=(α1,α2.…,αn),A∈Cn×n
对于α
1
\alpha_1
α1,存在一组Givens矩阵T
12
,
T
13
,
…
,
T
1
n
T_{12},T_{13},\dots,T_{1n}
T12,T13,…,T1n,使得

于是
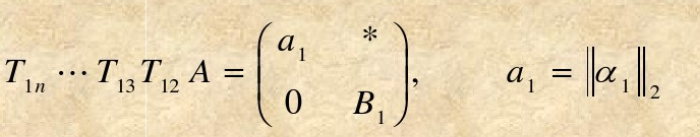
- 将矩阵
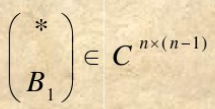
按列分块
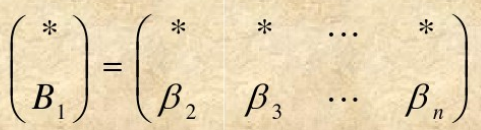
又存在一组Givens矩阵$T_{23},T_{24},\dots,T_{2n}
使得
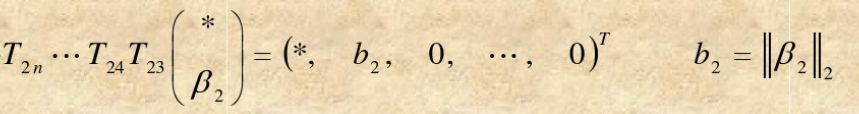
因此

依次进行 下去,得到
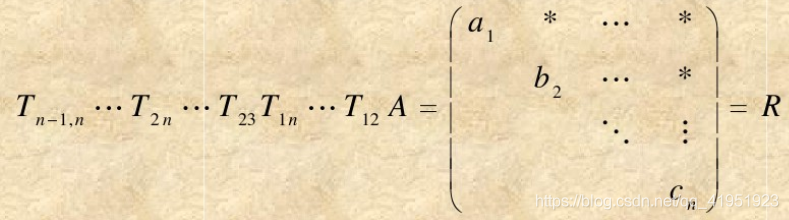
- 令
Q
=
T
12
H
…
T
1
n
H
T
23
H
…
T
2
n
H
T
34
H
…
T
n
−
1
,
n
H
Q = T_{12}^{H}\dots T_{1n}^{H} T_{23}^{H}\dots T_{2n}^{H}T_{34}^{H}\dots T_{{n-1},{n}}^{H}
Q=T12H…T1nHT23H…T2nHT34H…Tn−1,nH
则A
=
Q
R
A = QR
A=QR
注意: 利用Givens矩阵进行分解,需要作
n
(
n
−
1
)
2
\frac{n(n-1)}{2}
2n(n−1)个初等旋转矩阵的连乘积,当
n
n
n较大时,计算量较大,因此常用镜像变换Housholder变换来进行QR分解。
代码
#include<Eigen>
#include<iostream>
int main(int argc, char** argv)
{
Eigen::Matrix3d mat;
mat << 0, 3, 1, 0, 4, -2, 2, 1, 1;
std::cout << "原矩阵为:" << std::endl;
std::cout << mat<<std::endl;
Eigen::HouseholderQR<Eigen::Matrix3d>qr;
qr.compute(mat);
Eigen::Matrix3d Q, R;
Q = qr.householderQ();
R = qr.matrixQR().triangularView<Eigen::Upper>(); //上三角矩阵
std::cout << "结果Q:" << std::endl;
std::cout << Q << std::endl;
std::cout << "结果R:" << std::endl;
std::cout << R << std::endl;
system("pause");
return 0;
}
结果
原矩阵为:
0 3 1
0 4 -2
2 1 1
结果Q:
0 -0.6 -0.8
0 -0.8 0.6
-1 0 0
结果R:
-2 -1 -1
0 -5 1
0 0 -2