题目链接:
https://www.acwing.com/problem/content/description/241/
题目:
小 A 和小 B 在玩一个游戏。
首先,小 A 写了一个由 0 和 1 组成的序列 S,长度为 N。
然后,小 B 向小 A 提出了 M 个问题。
在每个问题中,小 B 指定两个数 l 和 r,小 A 回答 S[l∼r] 中有奇数个 1 还是偶数个 1。
机智的小 B 发现小 A 有可能在撒谎。
例如,小 A 曾经回答过 S[1∼3] 中有奇数个 1,S[4∼6] 中有偶数个 1,现在又回答 S[1∼6] 中有偶数个 1,显然这是自相矛盾的。
请你帮助小 B 检查这 M 个答案,并指出在至少多少个回答之后可以确定小 A 一定在撒谎。
即求出一个最小的 k,使得 01 序列 S 满足第 1∼k个回答,但不满足第 1∼k+1 个回答。
输入格式
第一行包含一个整数 N,表示 01 序列长度。
第二行包含一个整数 M,表示问题数量。
接下来 M 行,每行包含一组问答:两个整数 l 和 r,以及回答
even
或
odd
,用以描述 S[l∼r]中有偶数个 1还是奇数个 1。输出格式
输出一个整数 k,表示 01 序列满足第 1∼k个回答,但不满足第 1∼k+1 个回答,如果 01 序列满足所有回答,则输出问题总数量。
数据范围
N≤1e9,M≤10000
输入样例:
10 5 1 2 even 3 4 odd 5 6 even 1 6 even 7 10 odd输出样例:
3
方式1:并查集维护节点到根节点的距离,从而判断是否为同一类 (与之前并查集之 “食物链”的题目类似)
首先根据题目可以发现,N很大,1e9。 但是所用到的节点数为 2 * M , 2e4左右
所以可以想到与前面的并查集的应用之 “程序自动分析”一样 要用到离散化。
链接:
https://blog.csdn.net/qq_49120553/article/details/118760820?spm=1001.2014.3001.5501
同时可以发现此题的离散化 与 “程序自动分析”一样,不需要考虑离散化的值的顺序。
只是判断离散化的值 x 与 p[x]是否相同来判断是否为根节点,或者p[x]与p[y]是否在同一集合等等操作。 所以与顺序无关,使用哈希unordered_map 进行离散化即可。
而怎么使用并查集呢?
输入中会给出l,r 之间1的个数是奇数还是偶数。并且字符串只有1和0两部分组成。
那么我们可以使用前缀和的思想,如 l~r之间1的个数为奇数的话,
则 s[r] – s[l – 1]为奇数。 而这个的含义就是s[r] 与 s[l-1]一个为奇数一个为偶数。
同理 ,l~r之间1的个数为偶数的话
则s[r] – s[l – 1]为偶数,而这个的含义就是s[r] 与s[l – 1]要么两个都为奇数,要么两个都为偶数。
所以,也就可以通过奇偶性,如 l ~ r为奇数, 则s[r]与s[l – 1]不同类, l ~ r为偶数,则s[r]与 s[l – 1]同类 进行判断。
但是,这样的猜想是否正确呢?奇数个1,则两个不同类,偶数个1,则两个为同一类。
是正确的。因为我们可以发现,题目中并没有给出具体的字符串的形式。 所以只要你给出一个s[i]为奇数,或者偶数, s[ i – 1]为一个奇数 或者 偶数, 就可以构造出一种方式使得其成立
如: s[i]为奇数, s[i – 1]为偶数,也就是前 i – 1个中有偶数个1, 前i个中有奇数个1, 所以可以根据s[i],s[i – 1]的情况构造出一个a[i] 为 1 , 使得其成立
同样,s[i]为奇数,s[ i – 1]为奇数, 则a[i]为0。
所以,给出一个s[r], s[l]就一定至少一种方式可以构造出一个满足此s[r],s[l]的字符串出来。
所以此题就是用来判断,s[r] 与 s[l – 1] 是否为同类, 如前面推出s[r] 与 s[l – 1]为同类, 后面推出 s[r] 与 s[l – 1]不同类 ,则矛盾。
而判断两个节点是否同类就可以使用并查集。
分析:并查集 维护 节点到根节点的使用(与食物链题目类似)
应该怎么维护 根节点 到 节点 之间的距离呢?使用d[i],进行维护。
其中d[i]的含义是i节点到根节点之间的距离。
情况如下:
1.如果题目给出l~r中有偶数个1
则s[r] , s[l – 1]两者同类。
(1)r,l – 1在同一集合中,则d[r] + d[l – 1]为偶数即可。
分析:因为两个数相加,奇数 + 奇数 或者 偶数 + 偶数 才能为偶数
(2)不在同一集合中, 则将 l – 1的集合 并到 r的集合中去
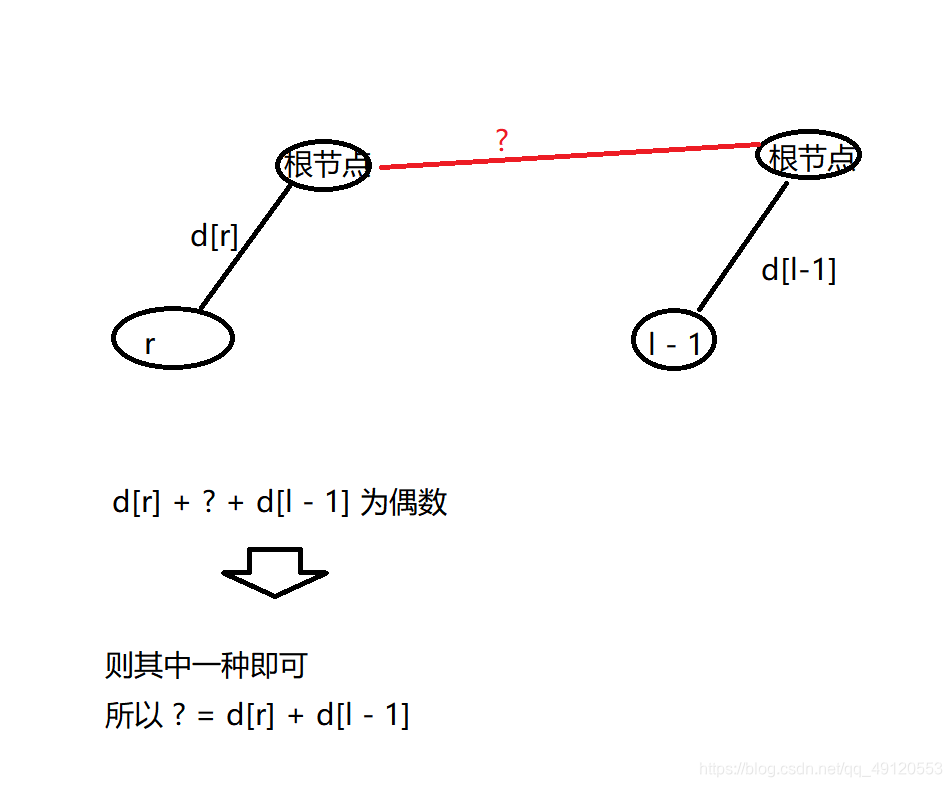
所以d[p[l- 1]] = d[r] + d[l – 1]
2.如果题目给出l~r中有奇数个1
则s[r] , s[l – 1]两者不同类。
(1)r,l – 1在同一集合中,则d[r] + d[l – 1]为奇数即可。
分析:因为两个数相加,偶数 + 奇数 才为奇数
(2)不在同一集合中, 则将 l – 1的集合 并到 r的集合中去
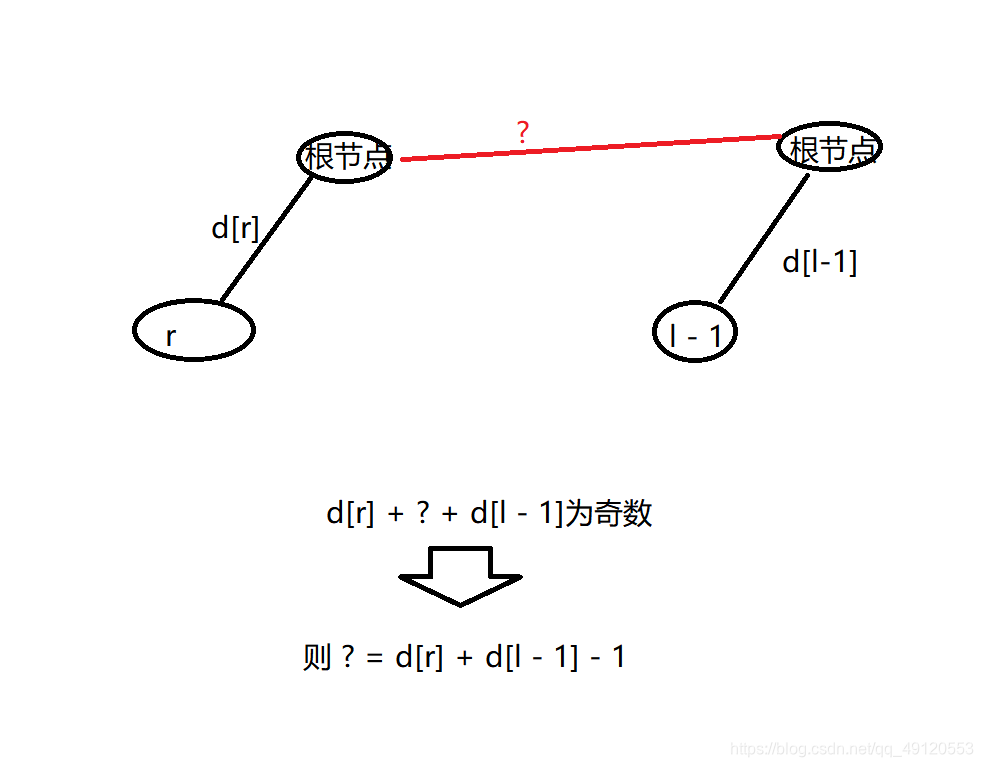
所以d[p[l- 1]] = d[r] + d[l – 1] – 1即可
代码:
# include <iostream>
# include <string>
# include <unordered_map>
using namespace std;
const int N = 20010;
int p[N];
int d[N]; // d[i]为 i节点 到 父结点 的距离。
unordered_map<int,int> h;
int idx;
int n,m;
int get(int x)
{
if(!h.count(x))
{
h[x] = ++idx;
}
return h[x];
}
int find2(int x)
{
if(p[x] != x)
{
int t = p[x];
p[x] = find2(p[x]);
d[x] += d[t];
}
return p[x];
}
int main()
{
scanf("%d %d",&n,&m);
for(int i = 1 ; i <= 2 * m ; i++)
{
p[i] = i;
d[i] = 0;
}
int cnt = m;
for(int i = 1 ; i <= m ; i++)
{
int a,b;
string ch;
cin >> a >> b >> ch;
int x = get(a - 1); // 因为l~r中1的个数,则s[r] - s[l - 1]为奇数
int y = get(b);
int px = find2(x);
int py = find2(y);
if(ch == "even") // 偶数
{
if(p[px] == p[py])
{
if( (d[x] + d[y]) % 2 != 0) // 不为偶数
{
cnt = i - 1;
break;
}
}
else //让x集合 接到 y的集合上
{
d[px] = d[x] + d[y];
p[px] = p[py];
}
}
else
{
if(p[px] == p[py])
{
if( (d[x] + d[y]) % 2 == 0)
{
cnt = i - 1;
break;
}
}
else
{
d[px] = d[x] + d[y] - 1;
p[px] = p[py];
}
}
}
printf("%d\n",cnt);
return 0;
}
方式2:扩展域并查集
扩展域并查集有一个核心的思路就是:合并多个条件,如果某个条件在这个集合中成立,则这个集合中的其他条件必须全部成立, 如果某个条件在这个集合中不成立, 则这个集合中的其他条件是否成立则无所谓。
而方式1则主要是合并两个节点,两个节点之间的关系则需要通过距离进行判断。
用不同的数值代表状态。r代表s[r]为偶数的情况,r + m 为 s[r]为奇数的情况
所以如:
(1)s[r] 与 s[l – 1] 是同类,
则合并r 与 l – 1. 并且合并 r + m , l – 1 + m.
即 合并s[r]为偶数,s[l – 1]也为偶数的情况, s[r]为奇数,s[l – 1]为奇数的情况。
(2) s[r] 与 s[l – 1]不是同类
则合并 r 与 l – 1 + m, 并且合并 r + m 与 l – 1
即 合并s[r]为偶数,s[l – 1]为奇数的情况, s[r]为奇数,s[l – 1]为偶数的情况。
这样合并后如何判断所给条件是否矛盾呢?
就用到了,集合中某个条件成立,则其他条件必须成立, 集合中某个条件不成立,则其他条件无所谓的性质。
s[r] 与 s[l – 1] 是同类
则说明 r,l – 1 在一个集合中, r + m , l – 1 + m 在一个集合中,
于是从中任意判断一个:如 p[r] 与 p[l – 1 + m] 是否在同一集合中。
(1)如果在同一集合中,则 r + m , 与 l – 1 + m 不在同一集合中,发生矛盾。
则说明 r 与 l – 1不是同类, 条件有矛盾。
(2)如果r 与 l – 1 + m 不在同一集合中, 则其他条件无所谓,因为其他的条件也一定不在同一集合中, 无法进行判断, 所以进行赋值,让它们在同一集合中即可,用于判断后面条件与当下这个条件以后是否会矛盾。
代码实现:
# include <iostream>
# include <unordered_map>
using namespace std;
const int N = 40010;
unordered_map<int,int> h;
int idx;
int p[N];
int get(int x)
{
if(h.count(x) == 0)
{
h[x] = ++idx;
}
return h[x];
}
int find2(int x)
{
if(x != p[x])
{
p[x] = find2(p[x]);
}
return p[x];
}
// x,y分别代表偶数, x + n , y + n 代表x,y分别为奇数
int main()
{
int n,m;
scanf("%d %d",&n,&m);
for(int i = 1 ; i <= 4 * m ; i++) //所有的l,r都会被离散化到M 以内,l和 l + m , r 和 r + m 共4种值,所以开4倍
{
p[i] = i;
}
int cnt = m;
for(int i =1 ; i <= m ; i++)
{
int l ,r;
string ch;
cin >> l >> r >> ch;
int x = get(l - 1);
int y = get(r);
if(ch == "even") //偶数
{
if(find2(x) == find2(y + m))
{
cnt = i - 1;
break;
}
else // 实际不用加else,但加else更容易让我自己看懂其中逻辑
{
p[find2(x)] = p[find2(y)];
p[find2(x + m)] = p[find2(y + m)];
}
}
else // 奇数,不同类
{
if(find2(x) == find2(y)) // 矛盾
{
cnt= i - 1;
break;
}
else
{
p[find2(x + m)] = p[find2(y)];
p[find2(x)] = p[find2(y + m)];
}
}
}
printf("%d\n",cnt);
return 0;
}