1 实验简介
R简介及线性回归实验
-
熟悉 R 语言基本语法
-
利用 R 语言完成线性回归
2 实验内容
2.1 混合同余法
利用如下递推公式:
x
n
=
(
a
x
n
−
1
+
c
)
m
o
d
m
x_{n} = ( ax_{n-1} + c ) \ mod \ m
x
n
=
(
a
x
n
−
1
+
c
)
m
o
d
m
用混合同余法产生 ,编写一个函数,并利用该函数计算:
如果
x
0
=
3
x_0 = 3
x
0
=
3
,
x
n
=
(
5
n
−
1
+
7
)
m
o
d
200
x_n = (5_{n-1} + 7 )\ mod \ 200
x
n
=
(
5
n
−
1
+
7
)
m
o
d
2
0
0
。求
x
0
,
x
1
,
.
.
.
,
x
10
x_0, x_1, …, x_{10}
x
0
,
x
1
,
.
.
.
,
x
1
0
基本思路
利用递推公式编写函数,依次代入
x
n
−
1
x_{n-1}
x
n
−
1
计算
x
n
x_{n}
x
n
,即可求得。
代码实现
f <- function(a, x, c, m) {
(a * x + c) %% m
}
x <- 3
for (i in 1:10) {
x <- f(5, x, 7, 200)
cat("x", i, ": ", x, "\n", sep = "")
}
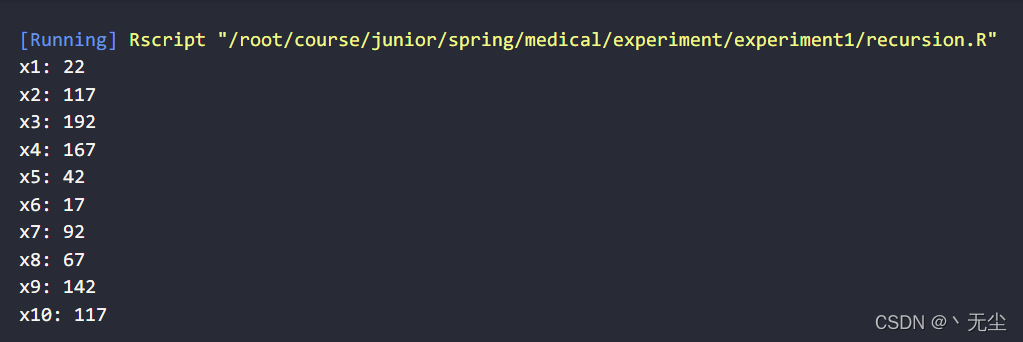
实验结果
运行以上代码,我们可以得到
x
0
,
x
1
,
.
.
.
,
x
10
x_0, x_1, …, x_{10}
x
0
,
x
1
,
.
.
.
,
x
1
0
,如下图:
2.2
π
\pi
π
的估计
考虑服从 (0,1) 区间上均匀分布的独立的随机变量,因此,二维随机变量 (X,Y) 的联合概率密度为:
f
(
x
,
y
)
=
{
1
,
0
<
x
<
1
,
0
<
y
<
1
0
,
o
t
h
e
r
w
i
s
e
f(x,y) = \begin{cases} 1, 0<x<1,0<y<1 \\ 0, otherwise \end{cases}
f
(
x
,
y
)
=
{
1
,
0
<
x
<
1
,
0
<
y
<
1
0
,
o
t
h
e
r
w
i
s
e
则
P
(
X
2
+
Y
2
<
=
1
)
=
π
4
P(X^2 + Y^2 <= 1) = \frac{\pi}{4}
P
(
X
2
+
Y
2
<
=
1
)
=
4
π
提示:产生均匀分布随机变量
runif()
基本思路
利用
runif()
函数生成 [0, 1] 上的均匀分布,计算满足公式 (3) 条件的点的频率,以此来估计
π
4
\frac{\pi}{4}
4
π
的值
代码实现
distance <- function(x, y) sum((x - y)^2)
f <- function(n) {
center <- c(0, 0)
pointMatrix <- matrix(runif(n * 2, min = 0, max = 1), nrow = n, ncol = 2, byrow = T)
distMatrix <- apply(pointMatrix, 1, distance, y <- center)
pi <- 4 * mean(distMatrix <= 1)
pi
}
实验结果
我们运行以上代码,可得到结果
| n | f(n) |
|---|---|
| 10 | 4 |
| 100 | 3.32 |
| 1000 | 3.08 |
| 10000 | 3.1436 |
| 100000 | 3.14732 |
| 1000000 | 3.143336 |
| 10000000 | 3.142091 |
我们可以看到,随着生成点数目的逐渐增加,
π
\pi
π
的估计值逐渐向真实值靠近
2.3 线性回归实验
糖尿病数据:有10个标准化的变量,另外一个是因变量 y,建立合适的线性回归方程进行拟合。
基本思路
如题,将包括年龄,性别,bmi 等前 10 列变量视作是自变量,将最后一列 y 视作是因变量,利用
lm()
模块进行线性回归建模
代码实现
data <- read.csv("medical/experiment/experiment1/diabetes.csv")
model <- lm(paste(names(data)[11], paste(names(data)[1:10], collapse="+"), sep = "~"), data)
print(summary(model))
实验结果
运行以上代码,得到结果:
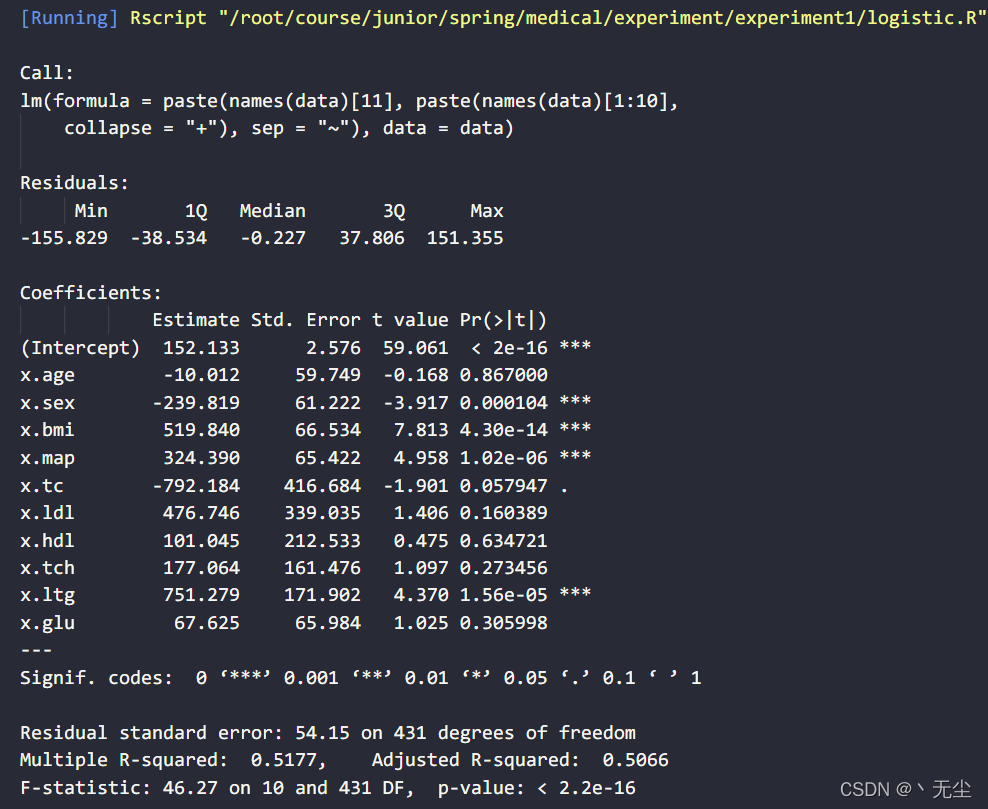
观察上述结果,我们可以发现:
- 残差项的中位数比较靠近 0,并且最大值最小值、1Q 与 3Q 的数值大小(绝对值)较为接近,说明残差分布较为对称、均匀,说明模型整体上较为充分的提取了自变量的信息。
- 拟合优度”和“修正的拟合优度”数值在 0.5 左右,说明回归方程对于数据的拟合程度较为一般
- F 统计量为 46.27,p-value < 2.2e-16 << 0.05,说明模型十分显著
- 在细节方面,sex,bmi,map,ltg 因素对于 y 值的影响较为显著,其他变量的影响不那么显著。每一个变量系数的标注差较大,说明数据分布不太均匀
- 综合以上几点,我们可以推测,线性模型对于该数据的变量信息提取比较充分,但拟合能力较为有限。不能很好的刻画原始数据的分布,后续可采用变换对数据进行预处理或者采用更为复杂的模型对数据作进一步的拟合
至此,本次实验完成。