1.1概念
因子分析法由斯皮尔曼在1904年首次提出,其在某种程度上可以被看成是主成分分析的推广和拓展。
因子分析法通过研究变量间的相关系数矩阵,把变量间错综复杂的关系归结成少数几个综合因子,由于归结出的因子个数少于原始变量的个数,但是他们又包含原始变量的信息,所以这一分析过程也称为降维。
因子往往比主成分更容易解释,所以因子分析比主成分分析更容易成功,从而有广泛的应用。
因子分析有两个核心问题:一是如何构造因子变量,二是如何解释因子变量
1.2应用背景
因子分析用于处理高斯数据,主要有两种情形
(1)
假设m个样本,样本的
维数
为n,如果n>>m,
此时非常困难拟合出高斯模型,因为自变量的维数远远超过自变量的个数,此时解有无数种,对于某一实际数据集合,往往样本对应的概率分布在客观上都是唯一的,我们无法用典型的概率分布准确表示出来。
(2)
m个样本的维度都较低,
用最大似然估计法去估计期望和方差,协方差矩阵是奇异的,即协方差矩阵不可逆,这在计算高斯分布是不可缺失的,除非m比n大一定较合适的值,否则对方差和均值的最大似然估计将会很难找到正确的值。
1.3因子分析的基本步骤
思路步骤
1.确定原有若干变量是否适合因子分析;
(变量之间是否有很强的相关性)
2.构造因子变量;
(
主成分法
、未加权最小平方法、综合最小平方法、
最大似然法
、
主轴因子法
、Alpha因子法、映像因子法)
3.利用旋转使得因子变量更具有可解释性;
(旋转分为正交旋转和斜交旋转,斜交旋转违背最初设定,可看作传统分析的拓展,
不论正交旋转还是斜交旋转,都应使新公共因子的绝对值尽可能接近0或1
)
4.计算因子变量的得分。
计算步骤
(1)相关性检验,一般采用KMO检验法和Bartlett球形检验法两种方法;
(2)输入原始数据Xn*p,计算样本均值和方差,对数据样本做标准化处理;
(3)计算样本的相关系数矩阵R;
(4)求相关系数矩阵R的特征值和特征向量;
(5)根据系统要求的累计贡献率确定公共因子的个数;
(6)计算因子载荷矩阵A;
(7)对载荷矩阵进行旋转,以求能更好地解释公共因子;
(8)确定因子模型;
(9)根据计算结果,求因子得分,对系统进行分析。
1.4构造因子变量中主要使用的方法
主成分法
:假设变量是因子的线性组合,第一主成分有最大的方差,后续主成分所解释的方差逐渐减小,各主成分之间互不相关,主成分法通常用来计算初始公因子,它也适用于相关矩阵为奇异时的情况。
最大似然法
:假设样本来自多元正态分布,使用极大似然估计。
主轴因子法
:从初始相关矩阵提取公共因子,并把多元相关系数的平方至于对角线上,再用初始因子载荷估计新的变量共同度,如此重复直至变量共同度在两次相邻迭代中的变化达到临界条件。
1.5因子分析中旋转的方法
在得到一个因子载荷矩阵的估计时,有可能会出现多个变量均在同一个因子上出现较大因子载荷,或者一个变量在多个因子上具有较大的载荷,此时很难对因子进行解释或命名,此时通过对因子载荷矩阵进行旋转得到新的简化后的因子载荷矩阵,便于因子分析和命名。
最大方差法
:一种正交旋转方法,它使得对每个因子有高负载的变量的数目达到最小。该方法简化了因子的解释。
直接Oblimin方法:一种斜交旋转方法,当delta等于0(缺省值)时,解是最斜交的,delta负得越厉害,因子的斜交度越低。要覆盖缺省得delta值0,请输入小于等于0.8的数。
最大四次方值法:它可使得解释每个变量所需的因子最少,该方法简化了观察到的变量的解释。
最大平衡值法:它是简化因子的最大方差法和简化变量的最大四次方值法的组合,它可以使得高度依赖因子变量的个数以及解释变量所需的因子的个数最少。
最优斜交法:速度快,可适用于大型数据集。
一般情况下,论文写作中使用最多的是最大方差法。
1.6 KMO检验和Bartlett球形检验法
KMO检验
KMO检验是Kaiser,Meyer和Olkin提出的,该检验是对原始变量之间的简单相关系数和偏相关系数的相对大小进行检验,主要应用于多元统计的因子分析。
KMO统计量是取值在0和1之间,当所有向量间的简单相关系数平方和远远大于偏相关系数平方和时,KMO值越接近1,意味着变量间的相关性越强,原有变量越适合作因子分析;反之越不适合。
其中,Kaiser给出一个KMO检验标准:KMO>0.9,非常适合;0.8<KMO<0.9,适合;
0.7<KMO<0.8,一般;0.6<KMO<0.7,不太适合;KMO<0.5,不适合。
Bartlett球形检验法
巴特利特球形检验是一种检验各个变量之间相关性程度的检验方法。一般在做因子分析之前都要进行巴特利特球形检验,用于判断变量是否适合用于做因子分析。
巴特利特球形检验是以变量的相关系数矩阵为出发点的。它的原假设是相关系数矩阵是一个单位阵(不适合做因子分析,指标之间的相关性太差,不适合降维),即相关系数矩阵对角线上的所有元素都是1,所有非对角线上的元素都为0。
巴特利特球形检验的统计量是根据相关系数矩阵的行列式得到的。如果该值较大,且其对应的p值小于用户心中的显著性水平(一般为0.05),那么应该拒绝原假设,认为相关系数不可能是单位阵,即原始变量之间存在相关性,适合于作因子分析。相反不适合作因子分析。
1.7因子分析得分的方法
1.回归法:一种估计因子得分系数的方法,生成的分数的平均值为0,方差等于估计的因子分数和真正的因子值之间的平方多相关性,即使因子是正交的,分数也可能相关。
2.Bartlett得分:所产生的分数的平均值为0,使整个变量范围中所有唯一因子的平方和达到最小。
3.Anderson-Rubin方法:它对Bartlett方法做了修正,从而确保被估计的因子的正交性。生成的分数平均值为0,标准差为1,而不相关。
在论文写作中,常使用第三种方法
2.1主成分分析与因子分析的区别
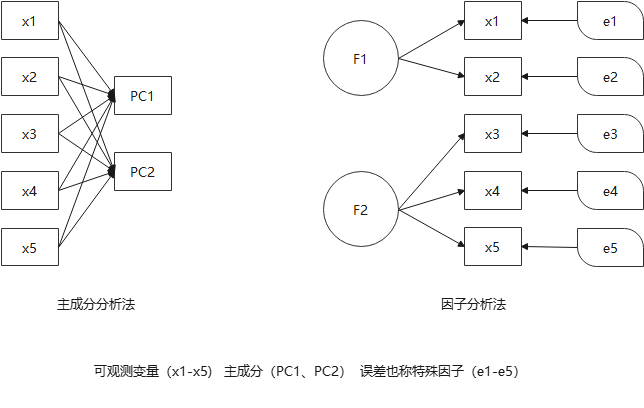
主成分分析不需要有假设,而因子分析需要假设各个共同因子之间不相关,特殊因子(specificfactor)之间也不相关,共同因子和特殊因子之间也不相关;
主成分分析的数量最多等于维度数;而因子分析中的因子个数需要分析者指定(SPSS和SAS根据一定的条件自动设定,只要是特征值大于1的因子主可进入分析),指定的因子数量不同而结果也不同。
主成分分析:当给定的协方差矩阵或者相关矩阵的特征值唯一时,主成分一般是固定的独特的;因子分析:因子不是固定的,可以旋转得到不同的因子。
对于因子分析,可以使用旋转技术,使得因子更好的得到解释,因此在解释主成分方面因子分析更占优势;其次因子分析不是对原有变量的取舍,而是根据原始变量的信息进行重新组合,找出影响变量的共同因子,化简数据;如果仅仅想把现有的变量变成少数几个新的变量(新的变量几乎带有原来所有变量的信息)来进入后续的分析,则可以使用主成分分析,不过一般情况下也可以使用因子分析。
2.2因子分析和主成分分析的使用
因子分析跟主成分分析一样,由于侧重点都是进行数据降维,因此很少单独使用,大多数情况下都会有一些模型组合使用。例如:
(1) 因子分析(主成分分析)+多元回归分析:判断并解决共线性问题之后进行回归预测;
(2) 因子分析(主成分分析)+聚类分析:通过降维后的数据进行聚类并分析数据特点,但因子分析会更适合,原因是基于因子的聚类结果更容易解释,而基于主成分的聚类结果很难解释;
(3) 因子分析(主成分分析)+分类:数据降维(或数据压缩)后进行分类预测,这也是常用的组合方法。
参考文献来源:
https://blog.csdn.net/iceberg7012/article/details/109054471
https://chuanchuan.blog.csdn.net/article/details/122738208
https://www.cnblogs.com/lantingg/p/9293880.html
https://www.cnblogs.com/liulunyang/p/3931685.htm