10. 机器人正运动学—姿态描述之欧拉角

1. 引言

2.6.4 欧拉角与旋转矩阵转换的C++实现

3. 总结

1. 引言

到目前为止我们基本已经讨论完了坐标系及变换相关的内容。前面我们一直在聊变换矩阵具备位姿描述的能力，它可以很清晰地描述两个坐标系之间的位姿关系，那么为什么还要单独再介绍关于姿态描述的内容呢？

显然是有原因的。没有哪一个工具是完美的，齐次变换矩阵也是如此。事实上在很多的场合用齐次变换矩阵是搞不定的，还记得我们在

4. 机器人正运动学—理解变换矩阵

中介绍的旋转矩阵的几个性质吗？旋转矩阵具有正交性，每一行每一列都具有单位长度，这引入了6个约束，因此旋转矩阵的9个元素实际上只有三个独立变量。想象一下这样的姿态描述会出现什么样的问题呢？

我们还是举一个简单的运动规划的例子来说明一下这个问题，假设你想让机器人的末端点从坐标A（0, 0, 0）直线移动到坐标B（1, 1, 1），不要在意参考坐标系是谁，就当是一个固定的世界系就好了。按照机器人的控制周期，我们需要每一个毫秒向机器人发送一个位置指令，那么这个问题怎么处理呢？显然我们不能一下子就给机器人发送B这个坐标点，因为这样机器人容易承受较大的电流冲击，这也就是运动规划的意义所在，我们需要在A和B之间插入一些中间点来减小冲击同时也能让机器人真正沿着AB之间的线段运动（如果不做插值机器人末端执行器实际走过的路径我们是不知道的）。以下是最简单的线性插值：

$P(t)=t\cdot\overrightarrow{AB},t\in [0,1]$

其中的t代表当前已经经历的时间的归一化值（假设要求2s到达，现在过了1s，那么t就是1s/2s=0.5）。关于运动规划我们后面再谈，有没有发现这个插值其实非常简单，我们有了起始位置，终止位置，很容易得到中间的插值点。

回过头来再看旋转矩阵，前面描述的实际是对平移的插值，旋转矩阵描述的是姿态，如果我们希望机器人末端执行器位置不变，姿态从初始的
$E$
变换到终止的
$R$
，请问我应该怎么找到每一时刻的中间变换呢？你可能没有答案。由于旋转矩阵的6个约束条件使得对旋转矩阵的插值几乎不可能。

以上例子说明为了能够实现姿态的有效插补我们只讨论旋转矩阵肯定是不行的，还需要其他关于姿态的更简单的表达，这也就是我们讨论姿态描述的初衷了。

除了旋转矩阵之外还有几种常用的用于进行姿态描述的方法：欧拉角，轴角，四元数。后面的几篇文章，我们将围绕着这几种姿态描述方法展开，本篇博客将介绍欧拉角。

2. 欧拉角

2.1 一点点体会

说些题外话，对于位置我们很容易找到它的描述方法，比如在笛卡尔坐标系下用
$x$
，
$y$
，
$z$
三个坐标值就可以很好的描述位置，位置的三个分量是非常容易解耦的。位置另外一个很好的特点是它的变换是满足交换律的。比如我先沿
$x$
轴平移1m，再沿
$y$
轴平移1m得到的变换与先沿
$y$
轴平移1m再沿
$x$
轴平移1m得到的变换是一样的。姿态就不同了，先绕
$x$
轴旋转45度，再绕
$y$
轴旋转45度对应的变换与先绕
$y$
轴旋转45度再绕
$x$
轴旋转45度对应的变换不是一种变换。

姿态变换不满足交换律！

这大概就是姿态描述要困难得多的原因。

想象一下既然旋转矩阵有六个约束即三个独立变量，那么我们可以怎样更简洁的描述姿态呢？你可能想到既然位置可以用三个坐标值来描述，那么姿态能不能用三个角来描述呢？你是对的，这就是欧拉角，由传奇人物欧拉首先提出。

2.2 欧拉角定义

欧拉角是能够唯一确定刚体姿态的三个独立的角变量。说白了就是用三个角度来描述刚体在坐标系中的姿态。从这个定义中我们看到欧拉角只规定了用三个独立的角变量，没有指明是哪三个角，也没有指明这些角如何定义。所以欧拉角的组合有很多种。

2.3
$ZXZ$
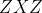
刚体系欧拉角

我们以绕新坐标系旋转的
$ZXZ$
欧拉角为例来说明。还是提前说一下，其实欧拉角的定义方式有两种，第一种是三个旋转均是相对于原始坐标系进行的(以后我们称这种欧拉角为

世界系欧拉角

)，第二种是三个旋转均是以前一次旋转得到的新坐标系为基础继续旋转(以后我们称这种欧拉角为

刚体系欧拉角

)。关于这一点在

6. 机器人正运动学—齐次变换矩阵的三种解读

中我们有相关的介绍。说明一下刚体系欧拉角和世界系欧拉角是我为了方便取的名字，这两种欧拉角更专业的名称我不清楚，如果哪位知道麻烦指点一下。

这里所谓的绕新坐标系旋转的
$ZXZ$
欧拉角就是刚体系欧拉角的一种，如下图是这种欧拉角对应的示意图。我来介绍一下这张图中的要素。

首先图中有蓝色的坐标系{0}和红色的坐标系{1}，我们研究坐标系的变换就在这两个坐标系之间进行。图中的蓝色和红色的椭圆（实际是圆）分别对应
$Ox_{0}y_{0}$
和
$Ox_{1}y_{1}$
两个平面。这两个平面的交线为N，我们称这个交线为节线。
$\alpha$
对应
$x_{0}$
与节线矢量的夹角，
$\beta$
对应
$z_{0}$
与
$z_{1}$
之间的夹角，
$\gamma$
对应节线矢量与
$x_{1}$
的夹角。

在这张图中坐标系{0}经历三次变换可以得到坐标系{1}。

坐标系{0}绕其自身
$z$
轴旋转
$\alpha$
得到坐标系{a}；
坐标系{a}绕其自身的
$x$
轴旋转
$\beta$
得到坐标系{b}；
坐标系{b}绕其自身的
$z$
轴旋转
$\gamma$
得到坐标系{1}。

图中为了简洁没有画出中间坐标系{a}和{b}。关于这个旋转过程的描述大家也可以看到，

每一次旋转都是绕前一次旋转得到的坐标系的轴进行旋转

。这三个变换对应的变换矩阵也应该是正着乘，即

$^{0}R_{1}=rot_{z}(\alpha )\cdot rot_{x}(\beta )\cdot rot_{z}(\gamma )$

2.4 RPY世界系欧拉角

世界系欧拉角也是三个角度，只不过对应的三次变换都是绕着世界坐标系旋转。在

6. 机器人正运动学—齐次变换矩阵的三种解读

我们也提到了当所有的变换都是以世界坐标系为参考，我们从点的操作算子角度去理解这些变换会更容易。

解释一下，RPY是roll（滚转），pitch（俯仰），yaw（偏航）的合写，分别代表了绕世界系
$x$
，
$y$
，
$z$
三个轴的旋转。在研究飞行器时这种姿态描述方法十分常用。下面图解一下RPY世界系欧拉角。以一个工字形作为要进行变换的刚体，如下图是刚体初始状态，此时刚体位于
$xoy$
平面内。

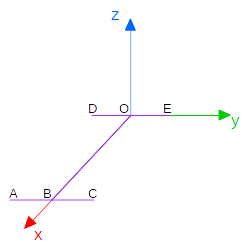
接下来我们进行Roll变换，也就是让刚体绕着世界系
$x$
轴旋转
$20^{\circ }$
，得到的状态如下图所示。

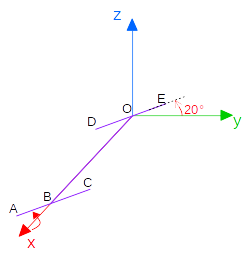
Roll变换相对来说是比较容易想象的一个变换，下面来看一下Pitch变换，如下图所示。

值得注意的是，Pitch变换是绕着世界系的
$y$
轴旋转。为了便于查看DE线段的旋转，我画了一些辅助线，虚线是刚体在进行Pitch变换之前的姿态。

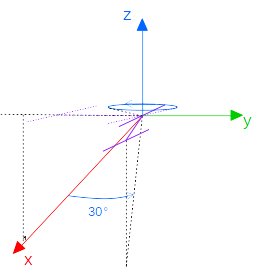
接下来我们来看Yaw变换，仍然要强调，Yaw变换是绕着世界系的
$z$
轴旋转，得到的结果如下图所示。

世界系欧拉角相对而言比较难作图，以上的几张图表现能力也是有限的。阐述了这么多关于刚体系欧拉角和世界系欧拉角的内容其实只是想传达一个内容：

刚体系欧拉角的三次旋转变换是相对于刚体系进行的（刚体系是动坐标系）而世界系欧拉角的三次变换都是相对于世界系进行的（世界系是固定坐标系）。

2.5 有多少组欧拉角？

前面我们也提到欧拉角并没有指定先绕哪一个轴旋转再绕哪一个轴旋转。所以你可以先绕
$x$
轴转再绕
$y$
轴转，你也可以先绕
$y$
轴转再绕
$x$
轴转。但是相邻的两次旋转不能是沿着同一个轴（这个很容易理解，如果两次旋转都是绕着同一个轴，那么就可以合并为一次旋转，角度是两次的旋转角相加）。那么这样的刚体系欧拉角有多少组呢？如果你还记得一点点排列组合的知识，应该能够写出下面的表达式：

$n=C_{3}^{1}\cdot C_{2}^{1}\cdot C_{2}^{1}=12$

同理世界系欧拉角也有12种。因此这样的欧拉角总共有24种，但是要提出一点，每一种刚体系欧拉角都有一种世界系欧拉角与其在数学意义上等价，我们举个例子（关于变换矩阵相乘的顺序问题可以参考

6. 机器人正运动学—齐次变换矩阵的三种解读

）：

1. 刚体系欧拉角先绕
$x$
轴转
$\alpha$
，再绕
$y$
轴转
$\beta$
，再绕
$z$
轴转
$\gamma$
，由于是刚体系欧拉角，变换关系要正着乘，因此对应的旋转矩阵为：

$R_{0}=rot_{x}(\alpha )\cdot rot_{y}(\beta )\cdot rot_{z}(\gamma )$

2. 世界系欧拉角先绕
$z$
轴转
$\gamma$
，再绕
$y$
轴转
$\beta$
，再绕
$x$
轴转
$\alpha$
，由于是世界系欧拉角，变换关系要倒着乘，因此对应的旋转矩阵为：

$R_{1}=rot_{x}(\alpha )\cdot rot_{y}(\beta )\cdot rot_{z}(\gamma )$

这个时候不难看出
$R_{0} = R_{1}$
。所以我依然倾向于认为欧拉角有12组。当然具体有多少组并不重要，大家只要明白这其中的道理就好了。

2.6 欧拉角与旋转矩阵之间的关系

前面我们都是在讨论欧拉角，在实际应用中，经常需要面对的是欧拉角和旋转矩阵之间的转换。先说一下欧拉角怎么转换为旋转矩阵，这个其实很容易，我们以
$ZXZ$
刚体系欧拉角为例。变换过程如下：

绕
$z$
轴转
$\alpha$
;
绕
$x$
轴旋转
$\beta$
;
绕
$z$
轴转
$\gamma$
。

2.6.1已知欧拉角求旋转矩阵

这个过程对应的旋转矩阵即为：

$R=rot_{z}(\alpha )\cdot rot_{x}(\beta )\cdot rot_{z}(\gamma )$

将旋转矩阵展开得到下式：

$R=\begin{bmatrix} C_{\alpha }C_{\gamma }-C_{\beta }S_{\alpha }S_{\gamma } & -C_{\alpha }S_{\gamma }-C_{\beta }C_{\gamma }S_{\alpha } & S_{\alpha }S_{\beta }\\ C_{\gamma }S_{\alpha }+C_{\alpha }C_{\beta }S_{\gamma } & C_{\alpha }C_{\beta }C_{\gamma }-S_{\alpha }S_{\gamma } & -C_{\alpha }S_{\beta }\\ S_{\beta }S_{\gamma } & C_{\gamma }S_{\beta } & C_{\beta } \end{bmatrix}$

为了方便以上公式进行了缩写，其中：
$C_{\theta }=cos(\theta )$
，
$S_{\theta }=sin(\theta )$
。以上就是有了欧拉角怎么写出旋转矩阵。这是一个正过程，是比较简单的。

2.6.2 已知旋转矩阵求欧拉角

已知了旋转矩阵求欧拉角稍微复杂了一些，原因是旋转矩阵到欧拉角并不是单射函数（实际上一个旋转矩阵可以对应到两组欧拉角的解）。为了限定欧拉角只有一组解，对三个旋转角度进行如下的限制：

$-\pi < \alpha \leq \pi;0\leq \beta \leq \pi ; -\pi < \gamma \leq \pi$

以上的限制告诉我们
$sin(\beta )\geq 0$
，设
$R(i,j)$
代表旋转矩阵
$R$
的第
$i$
行，第
$j$
列的元素。那么可以解得：

$\alpha =atan2(sin(\alpha ), cos(\alpha ))=atan2(R(1,3), -R(2,3))$

这里提一下
$atan2$
函数输入是一个角度的正弦和余弦，输出是角度值。（你应该也清楚已知了一个角度的正弦和余弦，那么在
$(-\pi ,\pi ]$
内这个角度取值是唯一的。C++等高级语言对这个函数均有API）。

值得注意的是
$atan2$
两个参数同时乘一个正的系数不影响这个函数的结果。（这个也容易理解，我们可以通过
$sin(\theta )^2+cos(\theta)^2=1$
辨识出这个正的系数）

。

$\beta$
的值可以从
$R(3,1)$
、
$R(3,2)$
和
$R(3,3)$
获取：

$sin(\beta )=\sqrt{R(3,1)^2 + R(3,2)^2}$
(由定义域已知
$sin(\beta )\geq 0$
)

$\beta =atan2(sin(\beta ),R(3,3))$

$\gamma$
的求解如下：

$\gamma =atan2(R(3,1), R(3,2))$

以上就是已知旋转矩阵求
$ZXZ$
刚体系欧拉角的公式，其他的欧拉角求解方式类似。

2.6.3 旋转矩阵转欧拉角的问题

上一节我们提到了旋转矩阵转欧拉角的公式，如果你仔细推导一下会发现在一些特殊的位置上以上公式是无解的。这些特殊位置指的就是当
$\beta = 0$
或者
$\beta =\pi$
时的情况。我们来解释一下为什么这种情况下无解。下图是当
$\beta = 0$
时三次变换的示意图

由于
$\beta = 0$
，第一次变换和第三次变换实际上是绕着初始坐标系的
$z$
轴旋转了两次，这种情况下我们只能确定
$\alpha + \gamma$
对应的角度却无法求解
$\alpha$
或者
$\gamma$
。下图是当
$\beta =\pi$
时三次变换的示意图

在这种情况下第一次和第三次旋转分别是绕着z和z”’，因为
$\beta =\pi$
，所以z和z”’两个轴共线，只是方向相反罢了。绕着这两个轴旋转，我们也是只能确定
$\alpha - \gamma$
。

$\beta = 0$
或者
$\beta =\pi$
实际对应的是一个奇异位置。这就是人们常说的欧拉角存在的问题，即万向节锁(gimbal lock)。
$ZXZ$
刚体系欧拉角可以与通常的六轴机器人的后三个关节一一对应。所谓
$\beta = 0$
或者
$\beta =\pi$
对应的是第五关节的角度，在这种情况下六轴机器人是奇异的。

2.6.4 欧拉角与旋转矩阵转换的C++实现

从
$ZXZ$
刚体系欧拉角到旋转矩阵的变换比较直接：

Rotation Rotation::eulerZXZ(double alpha, double beta, double gamma) {
  double sa, ca, sb, cb, sg, cg;
  sa = sin(alpha);
  ca = cos(alpha);
  sb = sin(beta);
  cb = cos(beta);
  sg = sin(gamma);
  cg = cos(gamma);

  return Rotation(ca * cg - cb * sa * sg, -ca * sg - cb * cg * sa, sa * sb,
                  cg * sa + ca * cb * sg, ca * cb * cg - sa * sg, -ca * sb,
                  sb * sg, cg * sb, cb);
}

从旋转矩阵到
$ZXZ$
刚体系欧拉角的变换如下：

void Rotation::getEulerZXZ(double &alpha, double &beta, double &gamma) const {
  double epsilon = 1E-12;
  if (fabs(data[8] > 1 - epsilon)) {
    gamma = 0.0;
    if (data[8] > 0.0) {
      beta = 0.0;
      alpha = atan2(data[3], data[0]);
    } else {
      beta = PI;
      alpha = atan2(data[3], data[0]);
    }
  } else {
    alpha = atan2(data[2], -data[5]);
    beta = atan2(sqrt(pow(data[6], 2) + pow(data[7], 2)), data[8]);
    gamma = atan2(data[6], data[7]);
  }
}

这里解释一下，data[8]代表的是
$R(3,3)$
，也就是
$cos(\beta )$
。我们通过data[8]与1的比较来判断
$\beta \rightarrow 0$
或者
$\beta \rightarrow \pi$
。在这两种情况下我们需要特殊处理，由于我们只能确定
$\alpha - \gamma$
或者
$\alpha + \gamma$
，不妨直接令
$\gamma = 0$
进而求解
$\alpha$
。注意这只是一种避奇异手段，当然我们也可以用其他手段，比如让
$\gamma$
取上一时刻的值，进而计算
$\alpha$
。旋转矩阵与
$ZXZ$
刚体系欧拉角的变换相关C++代码已上传至github：

https://github.com/hitgavin/rosws/tree/master/src/frames

。感兴趣的话可以阅读一下。

3. 总结

这篇文章主要介绍了欧拉角与旋转矩阵之间的关系。下一篇文章我们将介绍姿态的另一种描述方法：四元数。由于个人能力有限，所述内容难免存在疏漏，欢迎指出，欢迎讨论。

原文链接：https://blog.csdn.net/hitgavin/article/details/105210991

1. 引言

2. 欧拉角

2.1 一点点体会

2.2 欧拉角定义

2.3 刚体系欧拉角

2.4 RPY世界系欧拉角

2.5 有多少组欧拉角？

2.6 欧拉角与旋转矩阵之间的关系

2.6.1已知欧拉角求旋转矩阵

2.6.2 已知旋转矩阵求欧拉角

2.6.3 旋转矩阵转欧拉角的问题

2.6.4 欧拉角与旋转矩阵转换的C++实现

3. 总结

你可能也喜欢

2.3
$ZXZ$
刚体系欧拉角