博弈论
一、内容简介
本文主要介绍算法竞赛中常常出现的博弈论模型,包括:
- 4个经典组合游戏
- SG函数
- SG游戏及拓展
二、前置概念
进一步学习需要了解一些前置概念
- ICG
- 博弈图
- P点、N点
- mex函数
1.ICG
ICG全称为“公平组合游戏”,我们下面讨论的博弈游戏均建立在ICG的基础上,那么什么是ICG呢,它需要满足以下条件:
- 由两名玩家交替行动
- 对任意局面,接下来可执行的行动仅与局面有关(玩家平等)
- 游戏以玩家无法行动为结束,且无平局
那么称此游戏为“
公平组合游戏
”
2.博弈图
我们可以看到,整个过程是各个状态的集合,且状态间可以到达,那么我们可以将这个博弈过程抽象为一张图,称为
博弈图
,这个游戏我们也称之为
有向图游戏
那么这个图是一个有向无环图,图中有
唯一的起点
,可能有多个终点,两名玩家的交替行动可认为是图上的有向边,所有出度为0的节点便是终点
对于这个图,每个节点存储如下信息:{弈盘信息x,先手信息p,…}等
同时有如下结论:
任何一个公平组合游戏均可以转化为有向图游戏
3.P点、N点
P点和N点是博弈里面两个及其重要的概念
-
先手必胜状态
:先手行动后,可以将一个必败状态留给后手 -
先手必败状态
:先手无论如何行动,只能将必胜状态留给后手 -
必败点(P点)
:前一个选手取胜,当前选手将败的节点(previous) -
必胜点(N点)
:下一个选手将败,当前选手取胜的节点(next)
4.mex函数
mex函数是一个建立在集合上的整数函数,即
m
e
x
:
S
N
↦
N
mex: S_N \mapsto N
m
e
x
:
S
N
↦
N
,它的定义域是一个非负整数集,
m
e
x
mex
m
e
x
代表这个集合里最小未出现的非负整数,举几个例子:
m
e
x
(
{
1
,
2
,
3
}
)
=
0
mex(\{1,2,3\})=0
m
e
x
(
{
1
,
2
,
3
}
)
=
0
,
m
e
x
(
{
0
,
1
,
2
}
)
=
3
mex(\{0,1,2\})=3
m
e
x
(
{
0
,
1
,
2
}
)
=
3
,
m
e
x
(
{
0
,
2
,
3
}
)
=
1
mex(\{0,2,3\})=1
m
e
x
(
{
0
,
2
,
3
}
)
=
1
,等等
三、前置定理
定理一:没有后继状态的状态是必败状态
定理二:一个状态是必胜状态
⇔
\Harr
⇔
它至少存在一个向必败状态的转移
定理三:一个状态是必败状态
⇔
\Harr
⇔
它所有后继状态均为必胜状态
四、四大经典组合游戏
1.Nim游戏
给定
NN
N
堆物品,第
ii
i
堆物品有
Ai
A_i
A
i
个。两名玩家轮流行动,每次可以任选一堆,取走任意多个物品,可把一堆取光,但不能不取。
取走最后一件物品者获胜。
问先手是否必胜。
Nim博弈是最经典的博弈之一,许多博弈均可转化为Nim博弈,我们给出结论:
先手必胜
⇔
\Harr
⇔
A
1
⊕
A
2
⊕
A
3
.
.
.
⊕
A
n
≠
0
A_1\oplus A_2\oplus A_3…\oplus A_n\ne0
A
1
⊕
A
2
⊕
A
3
.
.
.
⊕
A
n
=
0
由归纳法其实很容易证得,也可以利用三个前置定理进行证明,但这个等价表达式还是给予我们很多震撼~~(也给予出题人很多灵感)~~
但其实我们不应把Nim游戏看成一个独立游戏,而应该把它看成若干个
游戏的和
对每个游戏,
先手是否必胜
⇔
\Harr
⇔
A
i
≠
0
A_i\ne0
A
i
=
0
进而对于这
n
n
n
个游戏的加和为
A
1
⊕
A
2
⊕
A
3
.
.
.
⊕
A
n
A_1\oplus A_2\oplus A_3…\oplus A_n
A
1
⊕
A
2
⊕
A
3
.
.
.
⊕
A
n
游戏和的概念后续还会继续用到,也是用异或的形式给出表达式,这个表达式很重要
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; ++ i) scanf("%d", &x), ans ^= x;
puts("%s", ans ? "Yes" : "No");
return 0;
}
2.Bash游戏
有 1 堆石子,总个数是
nn
n
。两名玩家轮流在石子堆中拿石子,每次至少取 1 个,至多取
mm
m
个。取走最后一个石子的玩家为胜者。
判定先手和后手谁胜。
给出结论:
先手必胜
⇔
\Harr
⇔
(
m
+
1
)
∤
n
(m+1)\nmid n
(
m
+
1
)
∤
n
考虑三种情形 :
情形一:
n
≤
m
n \le m
n
≤
m
时,显然先手必胜
情形二:
n
=
m
+
1
n=m+1
n
=
m
+
1
时,先手最多拿m个,但无论先手取走几个,后手一定可以拿完,后手胜
情形三:
(
m
+
1
)
∣
n
(m+1)\mid n
(
m
+
1
)
∣
n
时,假设先手每次拿
x
x
x
个,后手可以拿
m
+
1
−
x
m+1-x
m
+
1
−
x
个,最后后手胜
其余情形,先手均可以通过拿走
n
%
(
m
+
1
)
n \% (m+1)
n
%
(
m
+
1
)
个,进而转至情形三,先手胜
int main() {
scanf("%d%d", &n, &m);
puts("%s", n%(m+1) ? "First Win" : "Second Win");
return 0;
}
3.Wythoff游戏
有两堆石子,石子数可以不同。
两人轮流取石子,每次可以在一堆中取,或者从两堆中取走相同个数的石子,数量不限.
取走最后一个石头的人获胜。
判定先手是否必胜。
这个游戏的结论比较复杂,涉及到了平面上的点集,下图便是先手必败节点,
(
x
,
y
)
(x,y)
(
x
,
y
)
代表两堆石子个数

上面这张图粉色区域即为解集,解集是关于
y
=
x
y=x
y
=
x
对称,靠前的解有:
(
0
,
0
)
,
(
1
,
2
)
,
(
3
,
5
)
,
(
4
,
7
)
,
(
6
,
10
)
,
(
8
,
13
)
,
(
9
,
15
)
,
(
11
,
18
)
,
(
12
,
20
)
,
(
13
,
21
)
.
.
.
(0,0), (1,2), (3,5), (4,7), (6,10), (8,13), (9,15), (11,18), (12,20), (13,21)…
(
0
,
0
)
,
(
1
,
2
)
,
(
3
,
5
)
,
(
4
,
7
)
,
(
6
,
1
0
)
,
(
8
,
1
3
)
,
(
9
,
1
5
)
,
(
1
1
,
1
8
)
,
(
1
2
,
2
0
)
,
(
1
3
,
2
1
)
.
.
.
等
解集
(
a
k
,
b
k
)
(a_k,b_k)
(
a
k
,
b
k
)
满足 :
a
k
a_k
a
k
是之前未出现的最小自然数,
b
k
=
a
k
+
k
b_k=a_k+k
b
k
=
a
k
+
k
这个可以利用题目的性质进行归纳证明,主要利用了如下性质:
-
若
(x
,
y
)
∈
A
n
s
(x,y) \in Ans
(
x
,
y
)
∈
A
n
s
,那么
∀t
∈
N
,
(
x
+
t
,
y
)
∉
A
n
s
,
(
x
,
y
+
t
)
∉
A
n
s
,
(
x
+
t
,
y
+
t
)
∉
A
n
s
\forall t\in \N,(x+t,y)\notin Ans ,(x,y+t)\notin Ans,(x+t,y+t)\notin Ans
∀
t
∈
N
,
(
x
+
t
,
y
)
∈
/
A
n
s
,
(
x
,
y
+
t
)
∈
/
A
n
s
,
(
x
+
t
,
y
+
t
)
∈
/
A
n
s
我们称符合要求的解为奇异节点,奇异节点便是先手必败节点,而非奇异节点显然可以通过一步操作变成奇异节点,通过归纳法也可以证明奇异节点坐标正确性
按照解的定义,我们发现实际上集合
A
=
{
a
k
∣
k
∈
N
}
A=\{a_k|k\in \N\}
A
=
{
a
k
∣
k
∈
N
}
和
B
=
{
b
k
∣
k
∈
N
}
B=\{b_k|k\in \N\}
B
=
{
b
k
∣
k
∈
N
}
实际上是对整数区间的一个划分,即
A
∩
B
=
∅
,
A
∪
B
=
N
+
A\cap B=\varnothing,A\cup B=\N^+
A
∩
B
=
∅
,
A
∪
B
=
N
+
,考虑引入
Beatty定理
:
如果两个无理数
α,
β
\alpha,\beta
α
,
β
满足:
1α
+
1
β
=
1
\frac{1}{\alpha}+\frac{1}{\beta}=1
α
1
+
β
1
=
1
考虑两个正整数集
A,
B
A,B
A
,
B
:
A=
{
⌊
n
α
⌋
}
,
B
=
{
⌊
n
β
⌋
}
A=\{\lfloor n\alpha \rfloor\},B=\{\lfloor n\beta \rfloor\}
A
=
{
⌊
n
α
⌋
}
,
B
=
{
⌊
n
β
⌋
}
(1
)
(1)
(
1
)
以及两个结论:
A∩
B
=
∅
,
A
∪
B
=
N
+
A\cap B=\varnothing,A\cup B=\N^+
A
∩
B
=
∅
,
A
∪
B
=
N
+
(2
)
(2)
(
2
)
那么我们断言:
(1
)
⇔
(
2
)
(1)\Harr(2)
(
1
)
⇔
(
2
)
,可利用取整函数的上下界进行证明
将
Beatty定理
代入我们的解集,利用
β
=
α
+
1
\beta = \alpha +1
β
=
α
+
1
解出:
α
=
5
+
1
2
,
β
=
3
−
5
2
\alpha = \frac{\sqrt{5}+1}{2} ,\beta=\frac{3-\sqrt{5}}{2}
α
=
2
5
+
1
,
β
=
2
3
−
5
假设两堆石子为
(
a
k
,
b
k
)
,
a
k
<
b
k
(a_k,b_k),a_k \lt b_k
(
a
k
,
b
k
)
,
a
k
<
b
k
,那么
先手必败
⇔
\Harr
⇔
(
b
k
−
a
k
)
×
α
=
k
α
=
a
k
(b_k-a_k)\times \alpha =k \alpha = a_k
(
b
k
−
a
k
)
×
α
=
k
α
=
a
k
int main() {
scanf("%d%d", &n, &m);
if (a > b) swap(a, b);
int ans = (b - a) * ((1.0 + sqrt(5.0)) / 2.0);
puts("%s", ans==a ? "Second Success" : "First Success");
return 0;
}
4.Fibonacci游戏
有 1 堆石子,总个数是
nn
n
(n
≥
2
)
(n\ge 2)
(
n
≥
2
)
。游戏双方轮流取石子,规则如下:
先手不能在第一次把所有的石子取完,至少取 1 颗;
之后每次可以取的石子数至少为 1 ,至多为对手刚取的石子数的 2 倍。
取走最后一个石子的人为赢家,求必败态。
结论:
先手必败
⇔
\Harr
⇔
石子数为斐波那契数
必要性可由归纳法简要证出,充分性建立在
Zeckendorf定理
:
任何正整数均可以表示为若干个不连续的 Fibonacci 数之和
进而先手可以将石子划分成多堆不连续的斐波那契数的加和,先手先取走最小堆,然后可以通过操作,让后手来面临这些斐波那契堆,且每次后手不能取完,而先手可以取完,最后先手取完最后的石子,先手胜
int f[N], x;
map<int,bool>mp;
int main(){
fib[1] = 1, fib[2] = 1;
for(int i = 3;i <= 50; ++ i) f[i] = f[i-1] + f[i-2], mp[f[i]] = 1;
while(scanf("%d", &x) && x != 0)
puts(mp[x] == 1 ? "Second win" : "First win");
return 0;
}
五、SG函数
1.SG函数
SG函数是对博弈图中每一个节点或者说状态的评估函数,
S
G
:
s
t
a
t
e
↦
N
SG: state \mapsto N
S
G
:
s
t
a
t
e
↦
N
规定游戏终点的 SG 函数值为 0 ,即
S
G
(
e
n
d
)
=
0
SG(end)=0
S
G
(
e
n
d
)
=
0
,同时扩展规定一个游戏图的 SG 值为起点的 SG 值,即
S
G
(
G
r
a
p
h
)
=
S
G
(
s
t
a
r
t
)
SG(Graph)=SG(start)
S
G
(
G
r
a
p
h
)
=
S
G
(
s
t
a
r
t
)
在有向图游戏中,对每个节点
xx
x
,设从
xx
x
出发有
kk
k
个状态转移,分别到达节点
y1
,
y
2
,
.
.
.
,
y
k
y_1,y_2,…,y_k
y
1
,
y
2
,
.
.
.
,
y
k
,那么定义
SG
(
x
)
SG(x)
S
G
(
x
)
为
xx
x
的后继节点的
SG
SG
S
G
值集合取
me
x
mex
m
e
x
即:
SG
(
x
)
=
m
e
x
(
{
S
G
(
y
1
)
,
S
G
(
y
2
)
,
.
.
.
,
S
G
(
y
k
)
}
)
SG(x) = mex(\{SG(y_1),SG(y_2),…,SG(y_k)\})
S
G
(
x
)
=
m
e
x
(
{
S
G
(
y
1
)
,
S
G
(
y
2
)
,
.
.
.
,
S
G
(
y
k
)
}
)
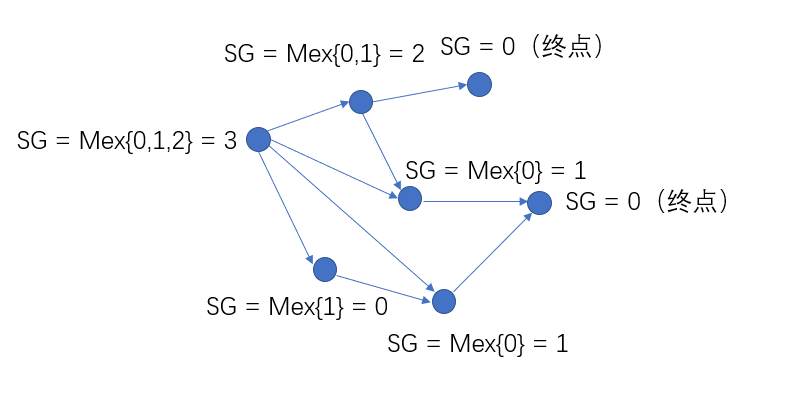
那么由前置定理,推出以下结论:
-
若
SG
(
x
)
=
0
SG(x)=0
S
G
(
x
)
=
0
,则为必败状态 -
若
SG
(
x
)
≠
0
SG(x)\not=0
S
G
(
x
)
=
0
,则为必胜状态
2.SG定理
SG 定理 :
对于游戏
XX
X
,它可以拆分成若干个子游戏
x1
,
x
2
,
.
.
.
,
x
n
x_1,x_2,…,x_n
x
1
,
x
2
,
.
.
.
,
x
n
,
X=
⋃
i
=
1
n
x
i
X = \bigcup_{i=1}^{n}x_i
X
=
⋃
i
=
1
n
x
i
那么,
SG
(
X
)
=
⊕
i
=
1
n
S
G
(
x
i
)
=
S
G
(
x
1
)
⊕
S
G
(
x
2
)
⊕
.
.
.
⊕
S
G
(
x
n
)
SG(X)=\oplus_{i=1}^{n}SG(x_i)=SG(x_1)\oplus SG(x_2)\oplus…\oplus SG(x_n)
S
G
(
X
)
=
⊕
i
=
1
n
S
G
(
x
i
)
=
S
G
(
x
1
)
⊕
S
G
(
x
2
)
⊕
.
.
.
⊕
S
G
(
x
n
)
换句话说,对于由
n
n
n
个有向图组成的组合游戏,设它们的起点为
s
1
,
s
2
,
.
.
.
,
s
n
s_1,s_2,…,s_n
s
1
,
s
2
,
.
.
.
,
s
n
当且仅当
S
G
(
s
1
)
⊕
S
G
(
s
2
)
⊕
.
.
.
⊕
S
G
(
s
n
)
≠
0
SG(s_1)\oplus SG(s_2)\oplus…\oplus SG(s_n) \not=0
S
G
(
s
1
)
⊕
S
G
(
s
2
)
⊕
.
.
.
⊕
S
G
(
s
n
)
=
0
时,这个游戏为先手必胜
证明方法与 Nim 游戏的证明类似
事实上,每一个简单
SG-组合游戏
都可以完全等效成一堆数目为
K
K
K
的石子,其中
K
K
K
为该简单游戏的 SG函数值。
定义
游戏的和
:考虑任意多个同时进行的 SG-组合游戏,这些 SG-组合
游戏的和
是这样一个SG-组合游戏:在它进行的过程中,游戏者可以任意挑选其中的一个
单一游戏
进行决策,最终,没有办法进行决策的人输。
易见,SG定理是对 游戏的和的SG值 和 单一游戏的SG值 间关系的一座桥梁,揭示了两者间的关系
3.简单应用
#include <unordered_set> // AcWing 893
int n, m, x, res;
int a[N], s[N], ans[M];
int sg(int x){//记忆化搜索
if(ans[x] != -1) return ans[x];
unordered_set<int>St;
for(int i = 1; i <= m; i++) if(x >= s[i]) St.insert(sg(x - s[i]));
for(int i = 0; ; i++) if(!St.count(i)) return ans[x] = i; // 求 mex
}
int main(){
scanf("%d", &m);
for(int i = 1; i <= m; i++) scanf("%d", &s[i]);// m 个起点
scanf("%d", &n);
memset(ans, -1, sizeof ans);
for(int i = 1; i <= n; i++) scanf("%d", &x), res ^= sg(x);
puts("%s", res ? "Yes" : "No");
return 0;
}
六、SG游戏及拓展
这一章节我们讲述 SG 游戏以及一些常见的扩展和应用,包括以下内容:
-
An
t
i
−
S
G
Anti-SG
A
n
t
i
−
S
G
游戏 -
Mu
l
t
i
−
S
G
Multi-SG
M
u
l
t
i
−
S
G
游戏 -
Ev
e
r
y
−
S
G
Every-SG
E
v
e
r
y
−
S
G
游戏 - 翻硬币游戏
- 无向图删边游戏
1.
A
n
t
i
−
S
G
Anti-SG
A
n
t
i
−
S
G
游戏
有
nn
n
堆石子两个人可以从任意一堆石子中拿任意多个石子,不能不拿,
拿走最后一个石子的人失败
求必胜策略
这个似乎与
S
G
SG
S
G
定理是相反的,
S
G
SG
S
G
函数建立在可执行决策上,它认为当可执行决策为空时(终点态)
S
G
SG
S
G
为 0 ,但这个游戏无法通过可执行决策来确切判断胜负,那我们是否要建立新的
S
G
SG
S
G
定理了呢
先给出结论:
先手必胜等价于
-
∀i
,
A
i
≤
1
&
S
G
(
X
)
=
0
\forall i,A_i \le 1 \space \& \space SG(X)=0
∀
i
,
A
i
≤
1
&
S
G
(
X
)
=
0
-
∃i
,
A
i
>
1
&
S
G
(
X
)
≠
0
\exist i,A_i \gt 1 \space \& \space SG(X)\not=0
∃
i
,
A
i
>
1
&
S
G
(
X
)
=
0
简证:第一点显然,对于第二点,若
S
G
(
X
)
≠
0
SG(X)\not=0
S
G
(
X
)
=
0
,先手每次操作使得其为 0 ,一直下去,使得最终只有一堆的石子数大于 1 ,此时,轮到先手操作,先手可以让局面变成只有奇数个 1 ,先手胜
其实除了全为 1 的情况,剩下情况还是符合常规
S
G
SG
S
G
定理的,我们分析一下
A
n
t
i
−
N
i
m
Anti-Nim
A
n
t
i
−
N
i
m
与常规
N
i
m
Nim
N
i
m
的区别,主要区别在于
S
G
(
X
)
=
0
SG(X)=0
S
G
(
X
)
=
0
时,我们无法判负,为解决这个几乎与常规
N
i
m
Nim
N
i
m
颠倒的博弈,我们引出下面的
S
J
SJ
S
J
定理
首先给出
A
n
t
i
−
S
G
Anti-SG
A
n
t
i
−
S
G
游戏的具体定义:
决策集合为空的游戏者获胜,生成终止局面的游戏者判负
其余规则与普通的
SG
SG
S
G
游戏相同。
再给出
S
J
SJ
S
J
定理:
对于任意一个
An
t
i
−
S
G
Anti-SG
A
n
t
i
−
S
G
游戏如果我们规定当局面中所有的单一游戏(不可再分割游戏)的
SG
SG
S
G
值为 0 时,游戏结束那么
先手必胜
等价于:(1)
∀i
,
S
G
(
x
i
)
≤
1
&
S
G
(
X
)
=
0
\forall i,SG(x_i)\le 1\space \& \space SG(X)=0
∀
i
,
S
G
(
x
i
)
≤
1
&
S
G
(
X
)
=
0
(2)
∃i
,
S
G
(
x
i
)
>
1
&
S
G
(
X
)
≠
0
\exist i,SG(x_i)\gt 1\space \& \space SG(X)\not=0
∃
i
,
S
G
(
x
i
)
>
1
&
S
G
(
X
)
=
0
证明与上述
A
n
t
i
−
N
i
m
Anti-Nim
A
n
t
i
−
N
i
m
类似
// Luogu P4279 Anti-Nim 模板题
int n, m, t, k;
int a[N];
int main(){
scanf("%d", &t);
while(t -- ) {
scanf("%d", &n);
int sg = 0, flag = 0;
for(int i = 1; i <= n; ++ i) {
scanf("%d", &a[i]), sg ^= a[i];
if(a[i] > 1) flag = 1;
}
if((flag == 0 && sg == 0) || (flag == 1 && sg != 0)) puts("John");
else puts("Brother");
}
return 0;
}
2.
M
u
l
t
i
−
S
G
Multi-SG
M
u
l
t
i
−
S
G
游戏
有
nn
n
堆石子两个人可以从任意一堆石子中拿任意多个石子,不能不拿
或者可以把一堆数量不少于
22
2
石子堆分为两堆不为空的石子堆无法操作的人失败
问谁有必胜策略
给出结论:
S
G
(
x
)
=
{
x
−
1
,
x
≡
0
(
m
o
d
4
)
x
,
x
≡
1
&
2
(
m
o
d
4
)
x
+
1
,
x
≡
3
(
m
o
d
4
)
SG(x)=\begin{cases} x-1 ,& x \equiv 0 \pmod 4 \\ x, & x \equiv 1 \&2 \pmod 4 \\ x+1, &x\equiv 3 \pmod 4 \end{cases}
S
G
(
x
)
=
⎩
⎪
⎨
⎪
⎧
x
−
1
,
x
,
x
+
1
,
x
≡
0
(
m
o
d
4
)
x
≡
1
&
2
(
m
o
d
4
)
x
≡
3
(
m
o
d
4
)
S
G
(
X
)
=
⊕
i
=
1
n
S
G
(
x
i
)
SG(X)=\oplus_{i=1}^n SG(x_i)
S
G
(
X
)
=
⊕
i
=
1
n
S
G
(
x
i
)
具体怎么来的,是依靠
独特的智慧
打表 来的,不过事实上,打表也确实是很重要 博弈类游戏 结论发现来源,不是所有人都有着拉马努金那种高超的直觉和经验
我们再来给出
M
u
l
t
i
−
S
G
Multi-SG
M
u
l
t
i
−
S
G
的准确定义:
Mu
l
t
i
−
S
G
Multi-SG
M
u
l
t
i
−
S
G
游戏规定,在符合拓扑原则的前提下,一个单一游戏的后继可以为 多个单一游戏 。
Mu
l
t
i
−
S
G
Multi-SG
M
u
l
t
i
−
S
G
其他规则与
SG
SG
S
G
游戏相同。
那么它有如下性质:
-
一个后继状态的SG值 为 后继状态中所能衍生出的所有独立游戏的异或和
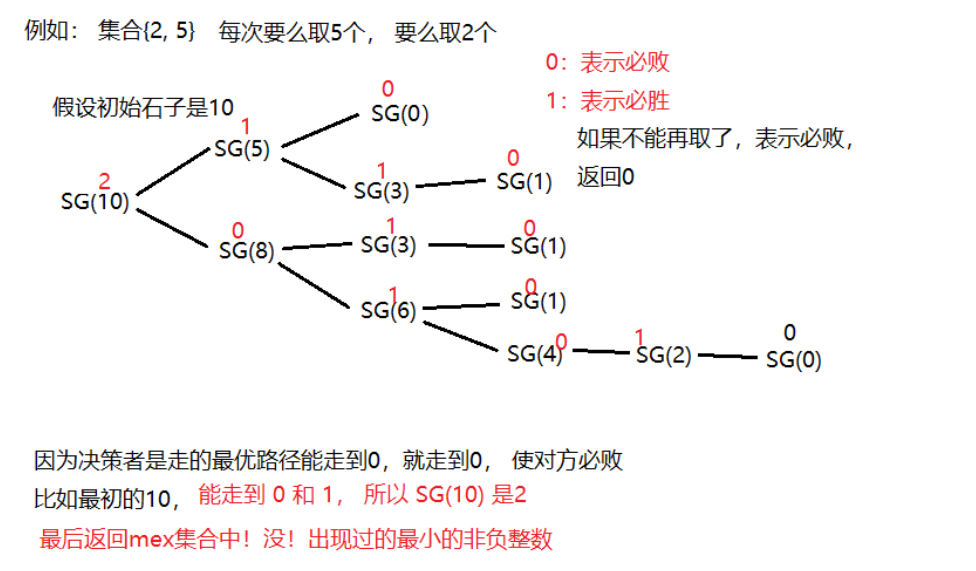
举个简单的例子:
S
G
(
3
)
SG(3)
S
G
(
3
)
的后继状态有
{
(
0
)
,
(
1
)
,
(
2
)
,
(
1
,
2
)
}
\{(0),(1),(2),(1,2)\}
{
(
0
)
,
(
1
)
,
(
2
)
,
(
1
,
2
)
}
也就是这堆有
3
3
3
个石子的石子堆,可以拿走或者分开等四种情况,他们的
S
G
SG
S
G
值分别为 $ { 0 , m e x { 0 } = 1 , m e x { 0 , 1 } = 2 , m e x { 0 , 1 , 2 } = 3 }$,因此 $SG(3)=mex{0,1,2,3}=4 $
int n, a[N], sg[N]; // hdu 3032 Multi-Nim 模板
int main(){
int t, scanf("%d", &t);
while(t -- ) {
int ans = 0;
scanf("%d", &n);
for(int i = 1; i <= n; ++ i) scanf("%d", &a[i]);
for(int i = 1; i <= n; ++ i) {
if(a[i] % 4 == 0) sg[i] = a[i] - 1;
else if(a[i] % 4 == 3) sg[i] = a[i] + 1;
else sg[i] = a[i];
ans ^= sg[i];
}
puts("%s", ans ? "Alice" : "Bob")
}
return 0;
}
int sg[M], vis[M]; // hdu 3032 打表代码
int main(){ // 对于一堆石子,数量为 M ,打表出 SG[M]
sg[0] = 0, sg[1] = 1;
for (int i = 2; i < M; ++ i){
memset(vis, 0, sizeof(vis));
//操作一,至少取一个
for (int j = 1; j <= i; ++ j) vis[sg[i - j]] = 1;
//操作二,分成两堆,不为空
for (int j = 1; j < i; ++ j) vis[sg[j] ^ sg[i - j]] = 1;
int j = 0; while (vis[j]) j ++ ;
sg[i] = j;
}
for (int i = 1; i <= M; ++ i) printf("sg[%d] : %d\n", i, sg[i]);
return 0;
}
3.
E
v
e
r
y
−
S
G
Every-SG
E
v
e
r
y
−
S
G
游戏
给定一张无向图,上面有一些“棋子”
每人每次必须将所有可以移动的棋子都进行移动
最后不能移动的人输
求是否有必胜策略
还有一道 杭电OJ (HDU-3595) 的题:
GG和MM喜欢玩游戏。在游戏开始时,有两堆石头。
MM首先选择一堆石头,里面有
xx
x
块石头,然后选择一个正数k,从另一堆有
yy
y
块石头的堆中取走
kx
kx
k
x
块石头
(y
≥
k
x
)
(y\ge kx)
(
y
≥
k
x
)
。然后是轮到了GG,也遵循上述规则选择石头。
当有人不能移除任何石头时,他就输掉了比赛,这个游戏就结束了。
很多年后,GG和MM发现这个游戏太简单了,所以他们决定一次同时玩
NN
N
个上述游戏。MM先手,当进入他的回合时,他必须对每个未完成的游戏进行操作。
取石头规则与上述相同,如果有人无法取走任何石头(即输掉最后一场结束游戏),那么他就输了
对于每个测试用例,输出获胜者的姓名
给出
E
v
e
r
y
−
S
G
Every-SG
E
v
e
r
y
−
S
G
游戏的具体定义:
Ev
e
r
y
−
S
G
Every-SG
E
v
e
r
y
−
S
G
游戏规定,对于还没有结束的单一游戏,玩家必须对该游戏进行一步决策
Ev
e
r
y
−
S
G
Every-SG
E
v
e
r
y
−
S
G
游戏的其他规则与普通
SG
SG
S
G
游戏相同
E
v
e
r
y
−
S
G
Every-SG
E
v
e
r
y
−
S
G
游戏与普通
S
G
SG
S
G
游戏最大的不同就是它多了一维:时间
对于
S
G
SG
S
G
值为0的点,我们需要知道最少需要多少步才能走到结束,
对于
S
G
SG
S
G
值不为0的点,我们需要知道最多需要多少步结束
所有游戏都是独立的,并且我们发现无法操作者输,而同时又在进行多个游戏。因此,我们知道胜负情况最终由最后结束的游戏的胜负情况觉定。
既然只与最后结束的游戏相关,那么我们便不会太在意除最后一个游戏外其他游戏的胜负。
而且又由于我们得同时操作所有柚子,所以,对于我们必胜的游戏,我们一定会想办法将其尽可能的向后拖,尽可能完的结束;反过来,对于我们必败的游戏,我们一定会让他尽可能早的结束。
那么,我们首先可以判定出所有位置是
N
N
N
点还是
P
P
P
点,然后按照判定决策我们按拖延方案走还是加速方案走。
这样我们用
s
t
e
p
step
s
t
e
p
变量来记录每个单一游戏的这个步数,有点像关键路径算法
s
t
e
p
(
u
)
=
{
0
,
u
∈
E
n
d
max
{
s
t
e
p
(
v
)
}
+
1
,
<
u
,
v
>
∈
E
,
u
∈
N
,
v
∈
P
min
{
s
t
e
p
(
v
)
}
+
1
,
<
u
,
v
>
∈
E
,
u
∈
P
step(u)=\begin{cases} 0 ,& u \in End \\ \max \{step(v)\}+1, & <u,v>\in E,u\in N,v\in P \\ \min\{step(v)\}+1, &<u,v>\in E,u\in P \end{cases}
s
t
e
p
(
u
)
=
⎩
⎪
⎨
⎪
⎧
0
,
max
{
s
t
e
p
(
v
)
}
+
1
,
min
{
s
t
e
p
(
v
)
}
+
1
,
u
∈
E
n
d
<
u
,
v
>
∈
E
,
u
∈
N
,
v
∈
P
<
u
,
v
>
∈
E
,
u
∈
P
给出必胜结论:
对于
Ev
e
r
y
−
S
G
Every-SG
E
v
e
r
y
−
S
G
游戏,
先手必胜
⇔\Harr
⇔
单一游戏中最大的
st
e
p
step
s
t
e
p
为奇数
结论建立在以下三条性质上,可以归纳地证明,或者显然地感觉出它们是对的:
-
对于所有的单一游戏,先手必胜状态的
st
e
p
step
s
t
e
p
值为奇数,先手必败状态的
st
e
p
step
s
t
e
p
值为偶数 -
设最大的
st
e
p
step
s
t
e
p
为
ma
x
s
max_s
m
a
x
s
,那么胜手可以保证该单一游戏最少会在
ma
x
s
max_s
m
a
x
s
步结束 -
设最大的
st
e
p
step
s
t
e
p
为
ma
x
s
max_s
m
a
x
s
,那么胜手可以保证他所有必败的游戏最多在
ma
x
s
max_s
m
a
x
s
步结束
然后下面解决 HDU-3595 的题目,不过最好先看下 HDU-1525
浅要说下 HDU-3595 中单一游戏
N
/
P
N/P
N
/
P
判定的结论,这个单一游戏的背景来源于
E
u
c
l
i
d
Euclid
E
u
c
l
i
d
游戏
,
假设
a≥
b
a\ge b
a
≥
b
,那么如果
a=
b
a=b
a
=
b
,先手必胜,如果
a%
b
=
0
a\%b=0
a
%
b
=
0
,先手必胜,而如果
b<
a
<
2
b
b<a<2b
b
<
a
<
2
b
的话,怎么取就已经定了,进而如果
a>
2
∗
b
a>2*b
a
>
2
∗
b
,那么先手可以决定谁先取到
b<
a
<
2
b
b<a<2b
b
<
a
<
2
b
这个状态,所以当
a>
2
∗
b
a>2*b
a
>
2
∗
b
时,先手必胜,只用讨论当
b<
a
<
2
b
b<a<2b
b
<
a
<
2
b
时最后谁胜
int n,m,sg[MAX][MAX],step[MAX][MAX]; // hdu 3595
int SG(int x,int y){
if(x > y) swap(x, y);
if(~sg[x][y]) return sg[x][y];
if(!x || !y) return sg[x][y] = 0;
int r = y%x, d = y/x;
if(d == 1){ // 此时操作唯一
sg[x][y] = SG(r,x) ^ 1;
step[x][y] = step[r][x] + 1;
return sg[x][y];
}else{ // 由上述说明知必胜
step[x][y] = SG(r,x) + 1 + step[r][x]; // (r,x)先手胜的话,需多一步决策
return sg[x][y] = 1;
}
}
int main(){
memset(sg, -1, sizeof(sg));
while(cin >> n){
int mx = 0, a, b;
while(n--){
cin >> a >> b; // 每个单一游戏的两堆石头数
SG(a, b);
mx = max(mx, step[a][b]);
}
puts("%s", mx&1 ? "MM" : "GG");
}
return 0;
}
4.翻硬币游戏
有
nn
n
枚硬币排成一排,依次编号
11
1
到
NN
N
,有的正面朝上,有的反面朝上,现在按照一定的规则翻硬币,
比如每次只能翻一枚或者两枚,或者每次只能翻动连续的几枚,
但是要求最靠右的硬币必须从正面被翻到了反面,
操作集合为空者负,
求必胜策略
给出结论:
当前局面的
S
G
SG
S
G
值是所有正面朝上的硬币单独存在时的
S
G
SG
S
G
值的异或和
结论的来源估计也是打表猜结论和归纳大法
不过这个结论可以直接用,配合状压或者别的算法可以出很多题目
5.无向图删边游戏
给定一个
nn
n
个节点的有根树,两人轮流删边,删去边之后,不和根节点联通的部分都会被移除
不能操作者输,
求必胜策略
给出结论:
叶子节点的
S
G
SG
S
G
值为
0
0
0
,其他所有节点的
S
G
SG
S
G
值为它所有儿子的
S
G
SG
S
G
值加
1
1
1
后的异或和
可以参考
克朗原理
的证明,配合归纳法,假设
n
n
n
节点树成立,那么
n
+
1
n+1
n
+
1
节点树也成立
同时,树的删边游戏可以进一步扩展,感兴趣的同学可以参考
F
u
s
i
o
n
P
r
i
n
c
i
p
l
e
Fusion \space Principle
F
u
s
i
o
n
P
r
i
n
c
i
p
l
e
七、致谢与感悟
忙活了一整天,终于完结撒花了
学到了很多东西,对其内在数学模型有了更深的了解,也熟悉了一些常见处理手段(打表、归纳)
同时也收集了许多关于
S
G
SG
S
G
函数应用的代码模板和应用模型,真的收获颇丰
下面给出一些有用的链接,在写作时参考了很多
- 《组合游戏略述——浅谈SG游戏的若干拓展及变形》贾志豪 本文参考了许多许多
-
博弈论ACM / OI_繁凡さん的博客
里面总结的特别全面 -
博弈论知识汇总 solvit
里面介绍了本文未提到的
Ni
m
K
NimK
N
i
m
K
和
St
a
i
r
N
i
m
StairNim
S
t
a
i
r
N
i
m
-
博弈论题目总结(一)
和
博弈论题目总结(二)
分别介绍了经典博弈和
SG
SG
S
G
函数应用的大量例题 -
博弈论总结_Ethan-Walker的博客
里面包含了 80 余道博弈习题,涉及了博弈的方方面面 -
ACM-ICPC中博弈论的一些小小总结_phython96的博客
也介绍了一些本文未出现的思想方法和模型