博客

6.6.1 生成树及其构造

生成树：所有顶点均有边连接再一起，但不存在回路。

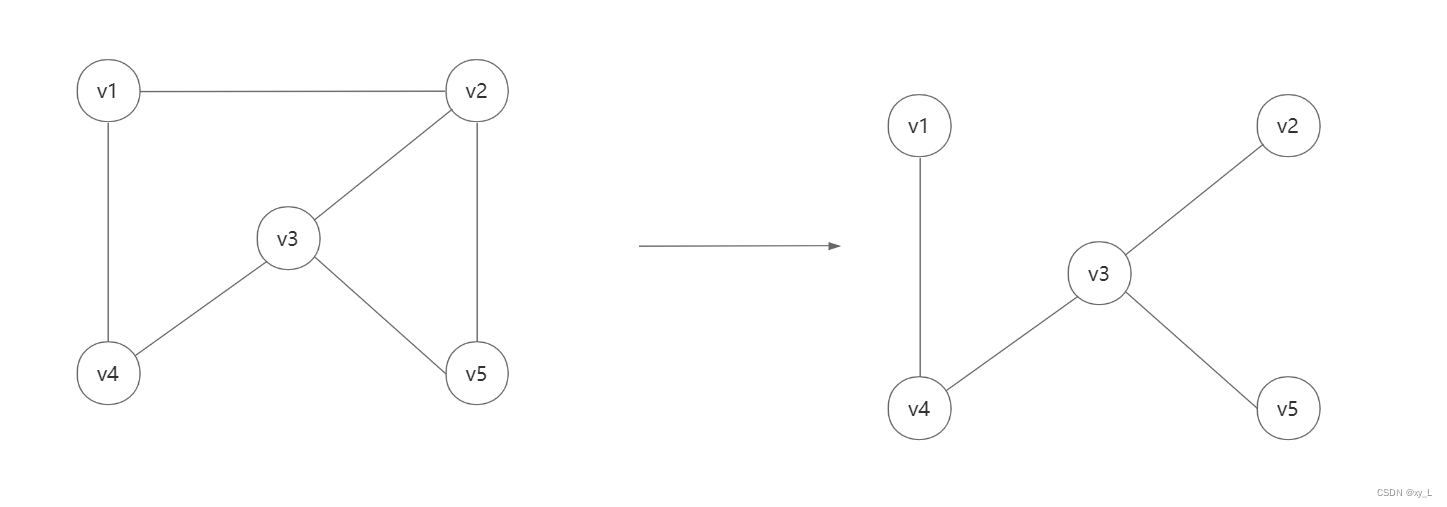
一个图可以有许多棵不同的生成树；所有生成树具有以下共同特点：

• 生成树的顶点个数与图的顶点个数相同；
• 生成树是图的极小连通子图，去掉一条边图是非连通的；
• 一个有n个顶点的连通图的生成树有n-1条边；
• 在生成树中再加一条边必然形成回路；
• 生成树中任意两个顶点间的路径是唯一的；
• 含有n个顶点n-1条边的图不一定是生成树。

无向图的生成树：

设图G = (V, E)是连通图，当从图任意顶点出发遍历图G时，将边集E(G)分成两个集合T(G)和B(G)，其中T(G)时遍历图时所经过的边的集合，B(G)时遍历时未经过的边的集合。因此，图G1(V, T)是图G的极小连通子图，即子图G1是连通图G的生成树。

6.6.2 最小生成树的定义

最小生成树：给定一个无向网络，在该网络的所有生成树中，使得各边权值之和最小的那棵生成树称为该网的最小生成树，也叫最小代价生成树。

6.6.3 构造最小生成树（Minimum Spanning Tree）

构造最小生成树的算法有很多，其中大多数算法都利用了MST的性质。MST性质：设N=(V,E)是一个连通图，V是顶点集V的一个非空子集，若边（u,v）是一条具有最小权值的边，其中v∈E，u ∈ V – U，则必存在一棵包含边（u, v）的最小生成树。

MST性质解析：

在生成树的构造过程中，图中n个顶点分属两个集合：

• 已落在生成树上的顶点集；
• 尚未落在生成树上的顶点集。

接下来则应在所有连通U中顶点和V – U中顶点的边中选取权值最小的边。

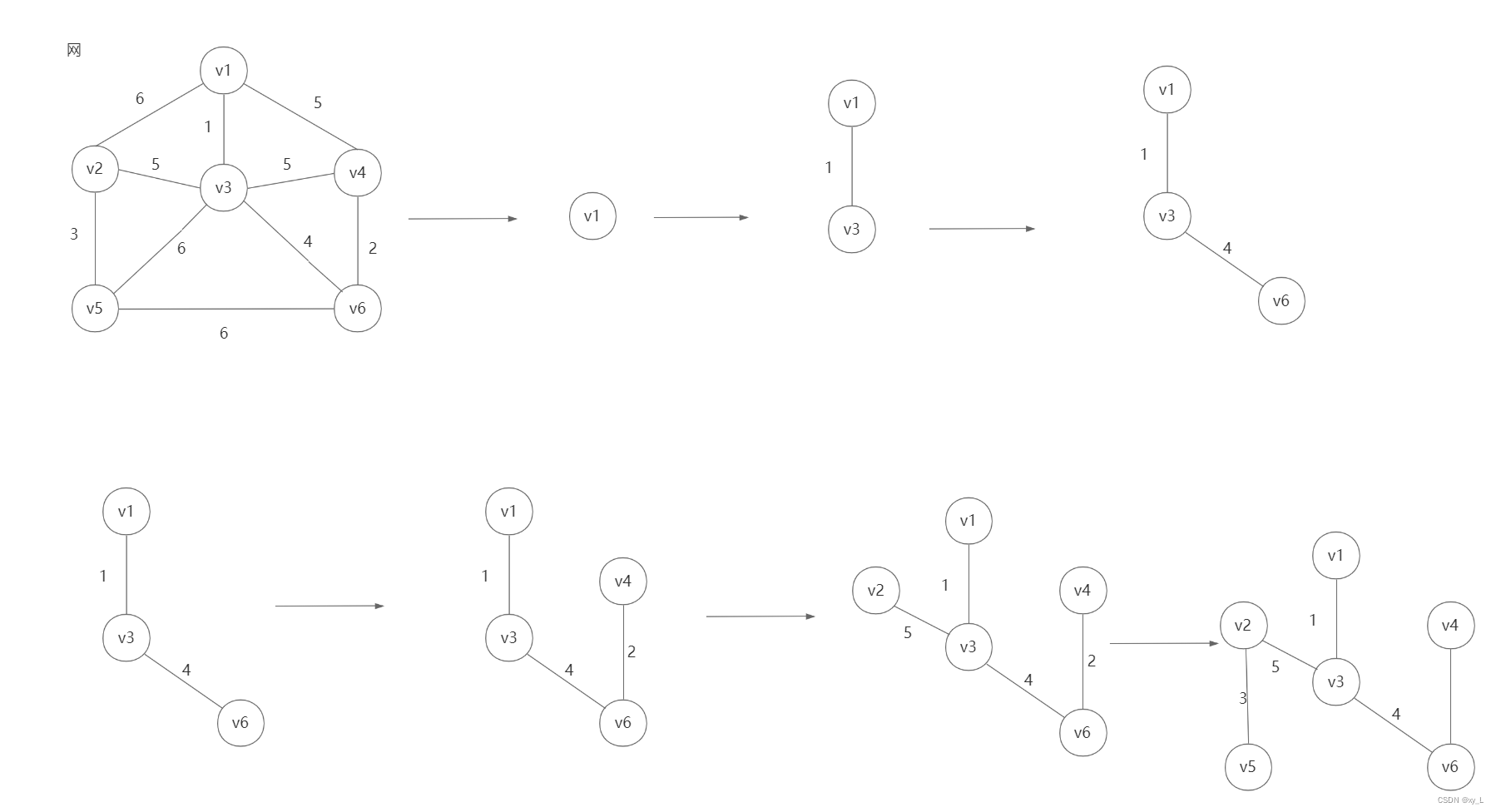
6.6.4 普里姆（Prim）算法

算法思路：

1. 设N = (V, E)是连通网，TE是N上最小生成树中边的集合；
2. 初始令U =  {u0}，(u0 ∈ V)，TE = {}；
3. 在所有u属于U，v = V-U的边（u,v）∈ E中，找一条代价最小的边（u0, v0）;
4. 将（u0,v0）并入集合TE，同时u0并入U；
5. 重复上述操作，直至U = V为止，则T=(U, TE)为N的最小生成树。

6.6.5 克鲁斯卡尔（Kruskal）算法

算法思路：

1. 设连通图N=（V,E），令最小生成树初始状态为只有n个顶点而无边的非连通图T = {V, {}}，每个顶点自成一个连通分量；
2. 在E中选取代价最小的边，若该边依附的顶点落在T中不同的连通分量上（即不能形成环），则将该边加入到T中；否则舍去此边，选取下一条代价最小的边；
3. 依次类推，直至T中所有顶点都在同一连通分量为止。

6.6.6 两种算法的比较

算法名称	普里姆（Prim）算法	克鲁斯卡尔（Kruskal）算法
算法思路	选择点	选择边
时间复杂度	（n为顶点数）	（e为边数）
使用范围	稠密图	稀疏图