3.快速排序及其优化
**并没有最好的排序算法,只有最适合的排序算法。**在面对不同规模的数据和不同排列的数据的时候,都有着适合当前数据的排序算法,一个好的排序算法就是面对合适的场景去选取最适合它的排序算法。
3.1 普通快速排序
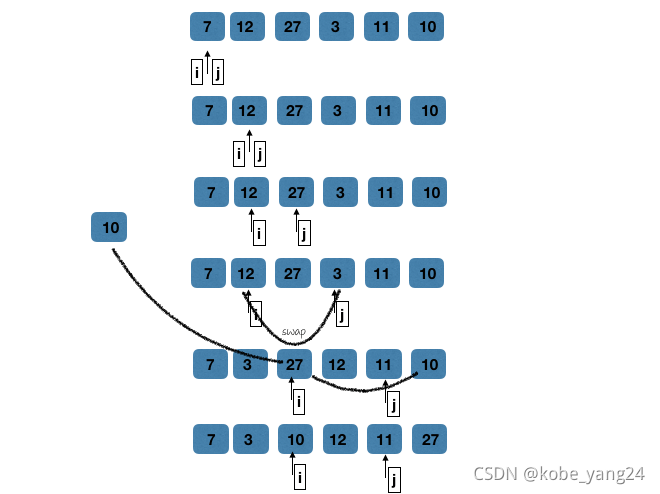
**快排的思想找到一个值使得数组左边的值都是小于等于它的数,数组的右边都是大于它的数。**然后继续去操作左右区间。可以看到,分成左右区间后,分别对不同的区间继续当前操作,
非常适合递归。
如上图所示,需要两个指针。
j 数组遍历的位置,i 第一个大于等于 选取的基准值的位置。
遍历,如果当前值小于基准值,判断两个指针是否相等,不等交换两个指针位置的值 ,都加1.
大于的话
j指针+1即可
。
1.普通快排一:
/**
* 最简单的 选取槽点的方法
* @param arr
* @param start
* @param end
* @return
*/
private int partition(int[] arr, int start, int end) {
// int temp = arr[end];
int temp = arr[end];
int j = start;
for (int i = start; i <=end; i++) {
if (arr[i] < temp) {
if (i != j) {
int a = arr[j];
arr[j] = arr[i];
arr[i] = a;
}
j++;
}
}
arr[j] = arr[end];
arr[end] = temp;
return j;
}
使用递归 排序数组
public void quickSort(int[] arr, int start, int end) {
if (start >= end) return;
int p = partition(arr, start, end);
quickSort(arr, start, p - 1);
quickSort(arr, p + 1, end);
}
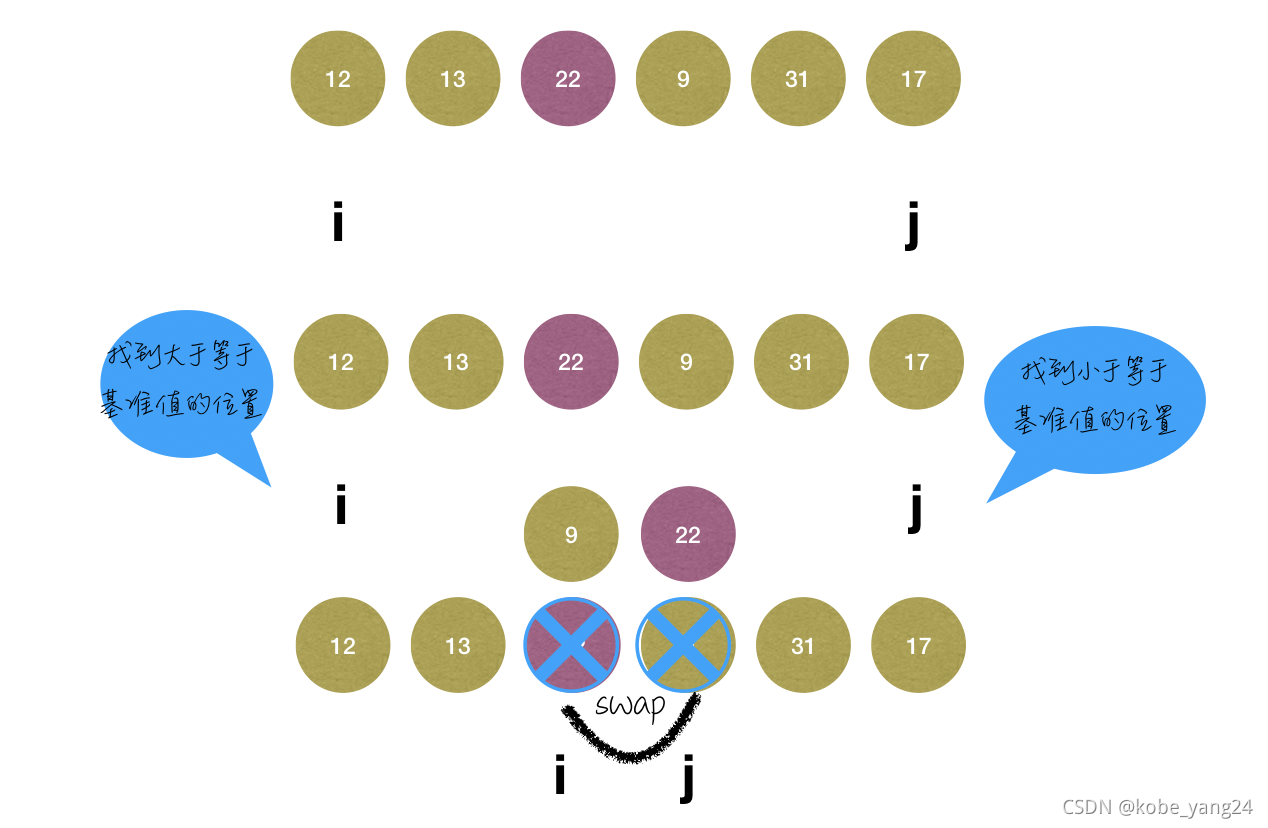
如上图所示为另外一种快排的解题思路左右两个指针,左边找到第一个大于等于基准值的位置,右边找到第一个小于等于基准值的位置。然后交换,直到循环结束。
这里槽位的选取 每次都是取 中间位置(如果遇到极端数据可以有效的提升系统的效率)
普通快排二:
public void quickSort1(int[] arr, int start, int end) {
int left = start;
int right = end;
int pivot = arr[(start + end) / 2];
while (left <= right) {
while (left <= right && arr[left] <= pivot) {
left++;
}
while (left <= right && arr[right] > pivot) {
right--;
}
if (left <= right) {
int temp = arr[left];
arr[left++] = arr[right];
arr[right--] = temp;
}
}
quickSort1(arr, start, right);
quickSort1(arr, left, end);
}
3.2 快速排序优化
3.2.1 选取基准值
三点去中法|随机法|中间位置法
**普通的快速排序遇见的第一个问题就是极端数据的问题,假设我们的数据已经是接近有序的,**每次选取的槽位都是数组的很大的数或者很小的数,那么我们每次递归的区间都接近于1 ,此时快速排序的时间复杂度就退化到了O(n^2).
普通排序二中我们选择了中间位置的方法,在leetcode上提交程序的效率得到了很大的提升。
三点取中法:
public int getMid(int a, int b, int c) {
if ((b - a) * (a - c) >= 0) {
return a;
} else if ((a - b) * (b - c) >= 0) {
return b;
} else {
return c;
}
}
但是需要注意的是 自己写的三点取中发后,程序的效率反而没有提升,这是因为每次多了很多的if判断,并且我们测试的数据也不是很大。
选取基准值得优化只是一种思想,目的是为了应对极端场景快速排序的效率降低的情况,我们也可有根据具体的场景去判断,去选择最优的选取基准值的方法。
3.2.2单边递归
3.2.3无监督partition
3.2.4 放弃快排
3.2.5 使用插入排序