博客

1. B树（B-tree、B-树）

B树是一种平衡的多路搜索树，多用于文件系统、数据库的实现。

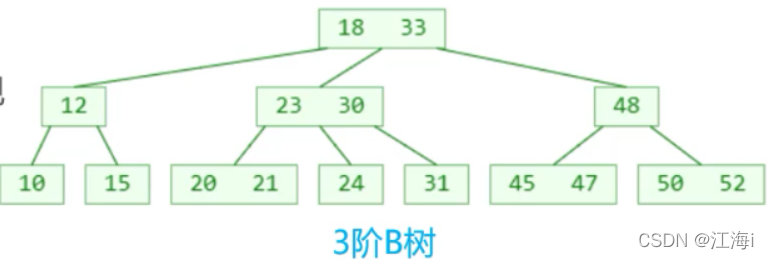
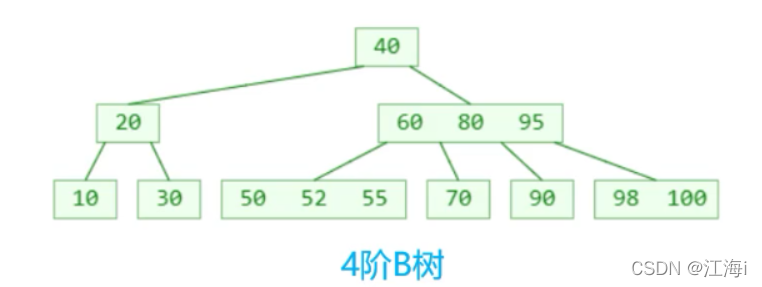
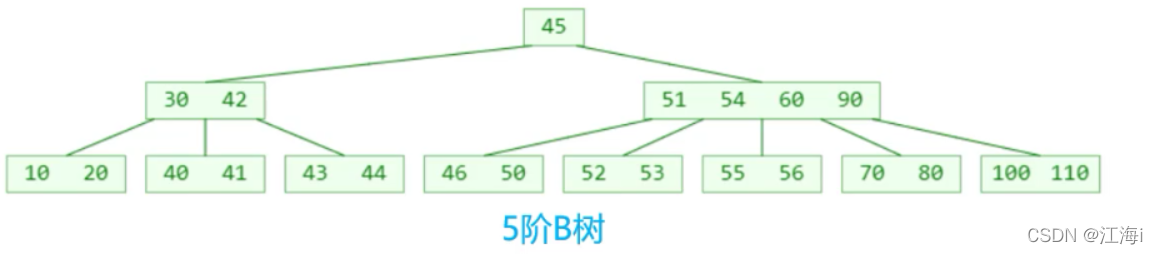
1.1 特点

1. 一个节点可以存储超过2个元素，可以拥有超过2个字节点；
2. 拥有二叉搜索树的一些性质；
3. 平衡：每个节点的所有子树高度一致；
4. 比较矮。

1.3 m阶B树的性质（m ≥ 2）

假设一个节点存储元素个数为X

1. 根节点：1 ≤ x ≤ m - 1
2. 非根节点：ceil(m / 2) - 1 ≤ x ≤ m -1 注：(ceil向上取整)。
3. 如果有子节点，子节点个数 y = x + 1
   ①. 根节点：2 ≤ y ≤ m
   ②. 非根节点：ceil(m / 2) ≤ y ≤ m

例如：

1. m = 3，2 ≤ y ≤ 3，则称为 （2，3）树或 2 – 3 树；
2. m = 4，2 ≤ y ≤ 4，则称为（2，3，4）树或者 2 – 3 – 4 树。
3. 类推…

1.4 B树和二叉搜索树

B树和二叉搜索树，在逻辑上是等价的。

超级节点： 多代节点合并。

1. 两代合并的超级节点，最多拥有四个子节点（至少是四阶B树）；
2. 三代合并的超级节点，最多拥有八个子节点（至少是八阶B树）；
3. 可以推导出：n代合并的超级节点，最多拥有 2 ^ n个节点（至少是 2 ^ n阶B树 ）。

m阶B树，最多需要log2m代合并。

1.5 搜索

根二叉搜索树的搜索类似。

1. 现在节点内部从小到大搜索；
2. 如果命中搜索结束；
3. 如果未命中，再去对应的子节点种搜索元素，重复步骤1。

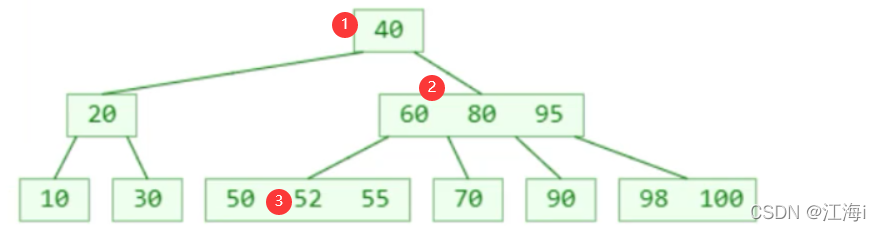
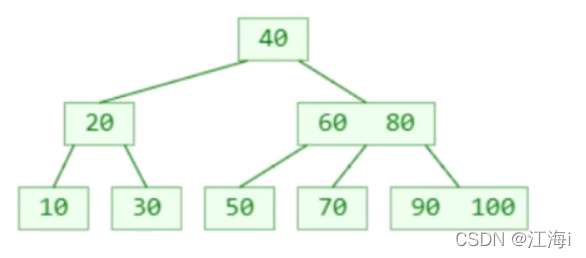
如图：寻找值为52的节点，从根节点开始，未命中，去右子节点中寻找，又未命中，去符合范围的最左侧子节点中找，命中就退出。

1.6 添加

新添加的元素必定是添加到叶子节点。

例如添加节点55：

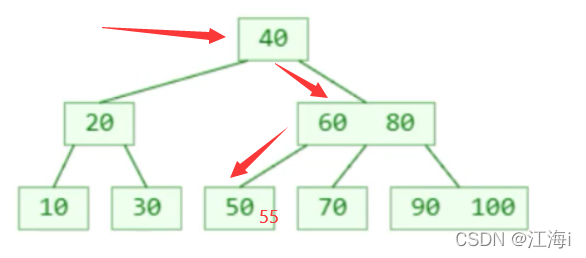
1.7 上溢

如图中是一个四阶B树，假设要添加一个元素98：

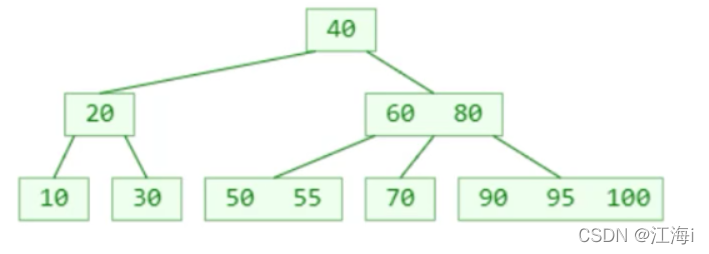
98应该放在下图所示位置，但这时超出了四阶B树可以存储的最多节点，这种现象称为上溢。

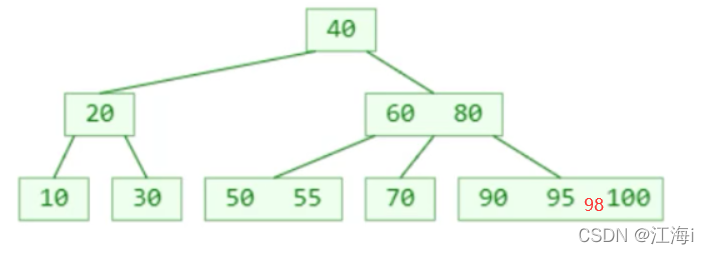
1.8 解决上溢

上溢节点的元素个数必然等于m；
假设上溢节点最中间元素的位置未k；

1. 将k位置的元素向上与父节点合并。
2. 将[0,k-1]和[k + 1 , m - 1]位置的元素分裂成两个子节点；
3. 但这种情况有可能导致父节点再次上溢，需要再将父节点合并，可能会持续到根节点，直到解决（这是一种唯一可以让B树长高的方法）。

解决上溢之后：

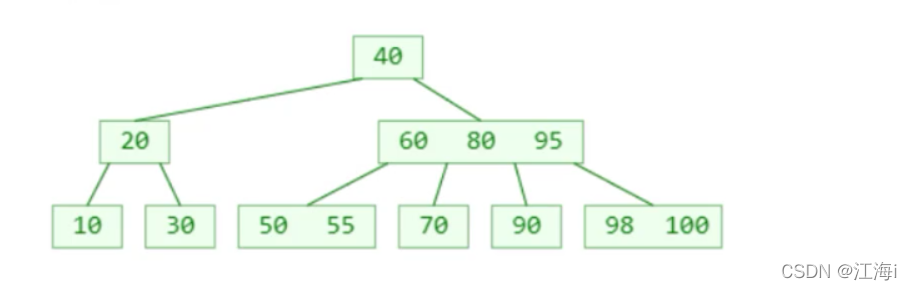
如图，再添加54节点：会导致当前节点和父节点都上溢。

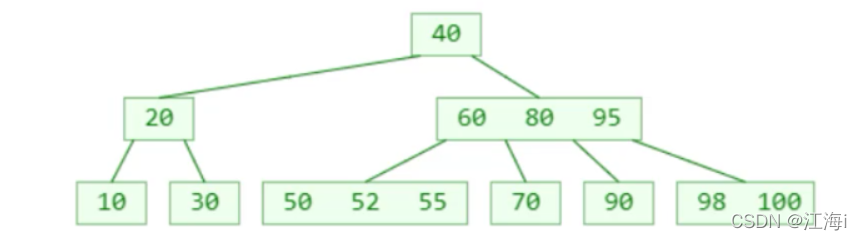
解决：将60上溢到根节点。

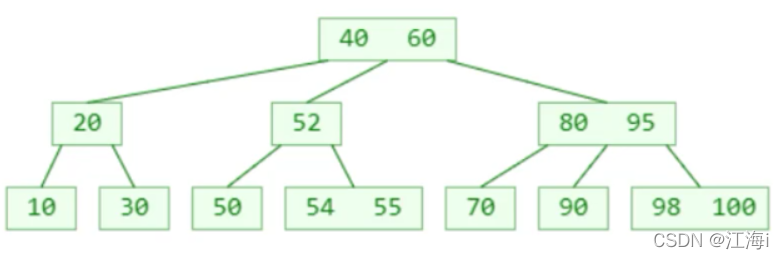
1.9 删除

1. 如果需要删除的元素在叶子节点中，直接删除即可。
   删除前：
   
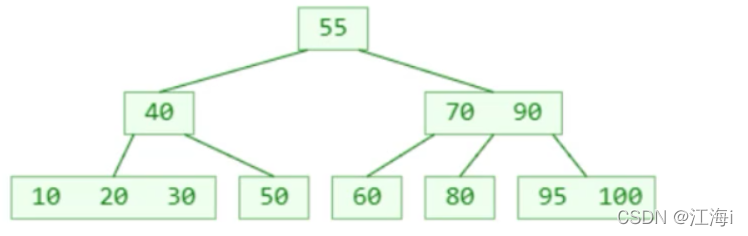
   删除后：
   
2. 非叶子节点：找到前驱或者后继元素，覆盖所需删除元素的值，再把前驱或者后继删除。
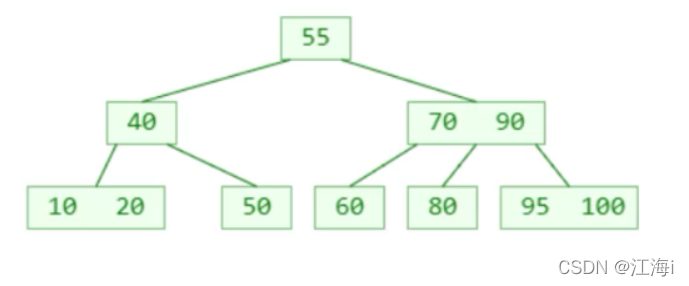
   删除前：
   
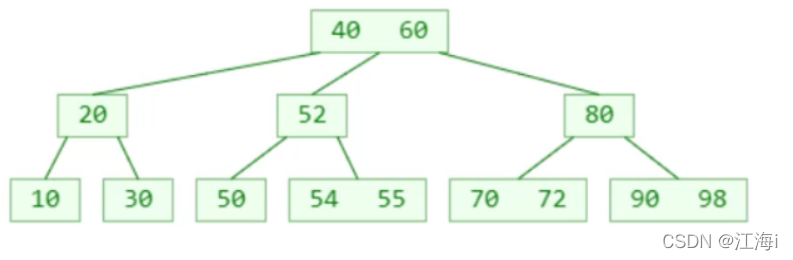
   找到前驱55执行覆盖，删除55：
   
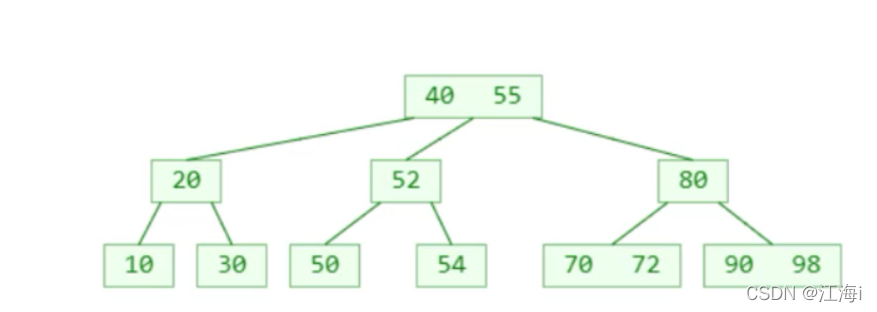
   非叶子节点的前驱和后继一定叶子节点中。，因此真正的删除是发生在叶子节点中的。

1.10 解决下溢

因为m阶B树的节点中最少存储ceil( m / 2) - 1个元素，发生删除时，如果小于改值就会发生下溢（underflow）。

产生下溢的节点元素数量必然等于 ceil( m / 2) - 2

解决方案：

1. 如果下溢的节点临近的兄弟节点，至少有ceil( m / 2)个元素，可以向它借一个（实际就是旋转）。
   ①. 将父节点的元素插入到下溢节点的最小位置；
   ②. 用兄弟节点的最大元素代替父节点的元素。
   

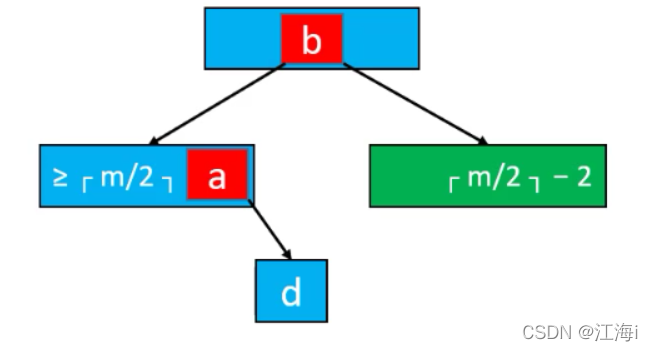
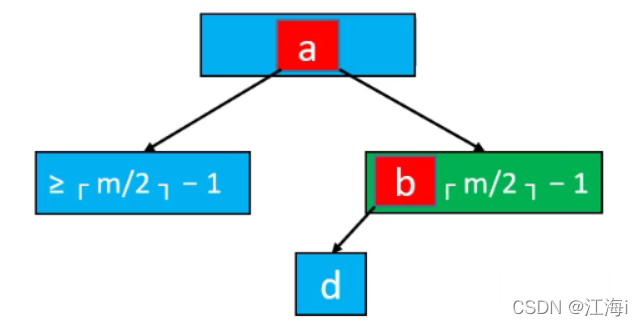
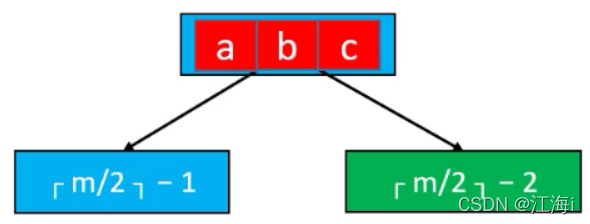
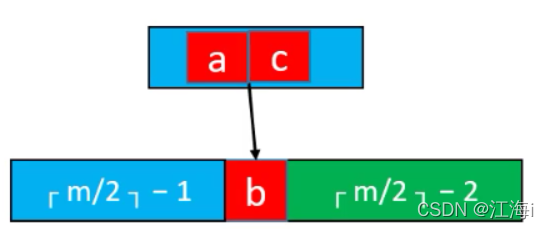
3. 如果临近的兄弟节点只有ceil( m / 2) - 1个元素：将父节点的元素挪下来与左右子节点合并；但是这种操作可能会导致父节点下溢，最坏的情况会导致一直持续到根节点需要通过这种方式解决（可能会导致B树高度减少）。