概要

四边形不等式的核心在于

缩小最优转移的范围

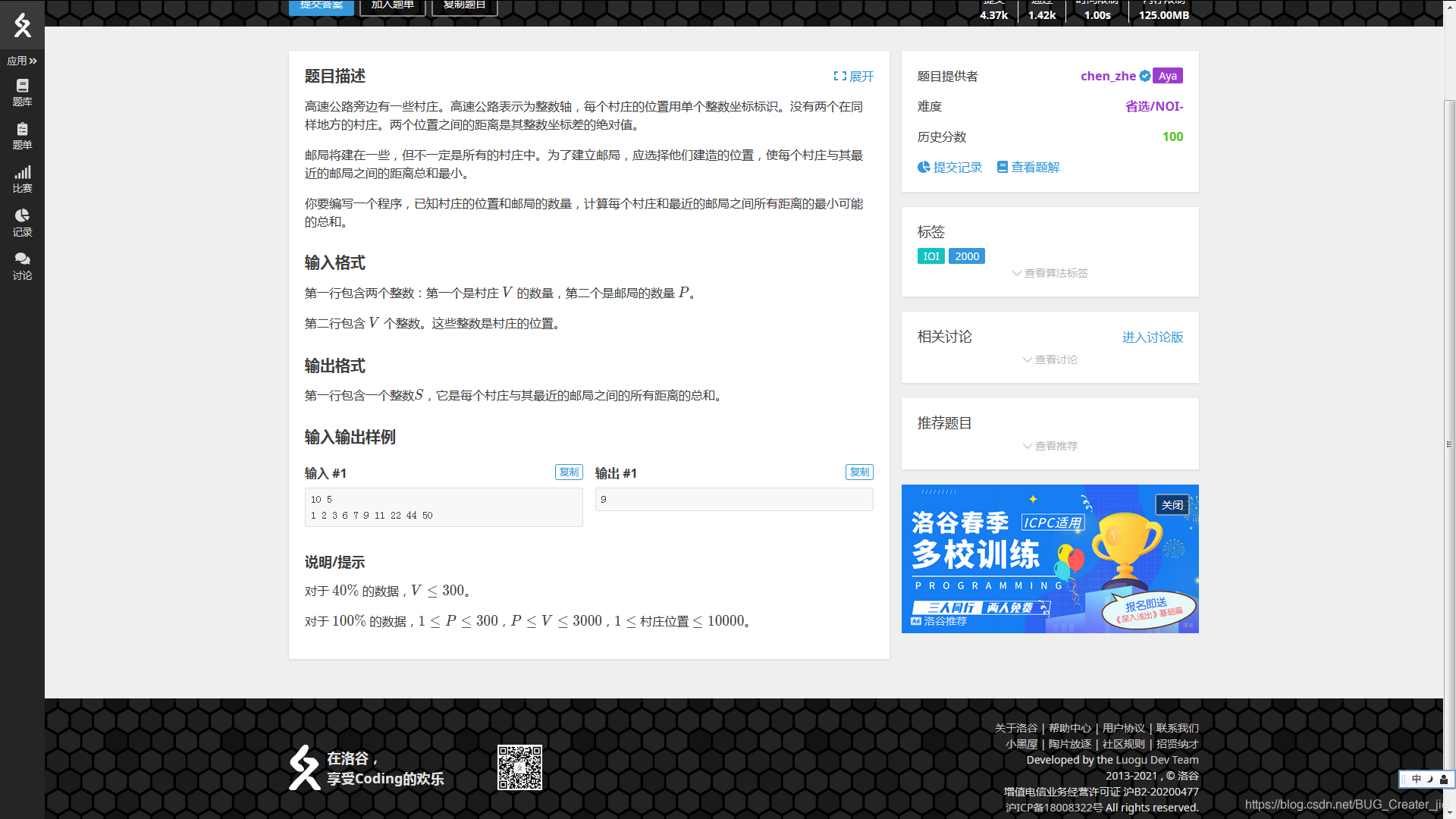
题目描述

传送门

解析

这道题说是不等式，但其实也可以感性理解


（其实就是不想证明）


定义pl[i][k]:

i到n的村庄建造k座邮局时，第一座管辖的范围是i-pl[i][k]

(也就是最优决策的转移点）

那么不难发现：

当新加一座邮局时，pl的值只可能变小

i向后移动一位时，pl的值只可能变大

抽象一下就是：

pl[i]k]<=pl[i][k-1]

pl[i][k]>=pl[i-1][k]

这样就缩小了转移的范围

达到了优化的目的

转移时一直记录最优转移点pl即可

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace  std;
const int N=3050;
#define ll long long
int n,m,a[N];
ll dp[N][350];//i,k表示起点为i，终点为n 
ll mid[N][N];
int pl[N][N];
void solve() {
	for(int l=1;l<=n;l++) {
		mid[l][l]=0;
		for(int r=l+1;r<=n;r++) {
			mid[l][r]=mid[l][r-1]+a[r]-a[l+r>>1];
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
	}
	solve();
	for(int i=1;i<=n;i++) dp[i][1]=mid[i][n],pl[i][1]=n;
	for(int k=2;k<=m;k++){
		for(int i=1;i<=n;i++){
			dp[i][k]=2e15;
			for(int p=pl[i-1][k];p<=pl[i][k-1];p++){
				if(dp[i][k]>mid[i][p]+dp[p+1][k-1]){
					dp[i][k]=mid[i][p]+dp[p+1][k-1];
					pl[i][k]=p;
				}
//				printf("p=%d mid=%lld dp2=%lld\n",p,mid[i][p],dp[p+1][k-1]);
			}
//			printf("p[%d][%d]=%d p[%d][%d]=%d pnow=%d k=%d i=%d dp=%lld\n\n",
//			i-1,k,pl[i-1][k],i,k-1,pl[i][k-1],pl[i][k],k,i,dp[i][k]);
		}
	}
	printf("%lld\n",dp[1][m]);
}