一、质数
二、约数
三、欧拉函数
四、快速幂
五、扩展欧几里得算法
六、中国剩余定理
七、高斯消元
八、组合计数
九、容斥原理
十、简单博弈论
一、质数
质数
质数,在大于1的整数中,有且只有1和他本身两个因数的数,也叫做素数
试除法判定质数
1、sqrt(x),函数计算的时间比较高
bool is_prime(int x)
{
// 质数大于1
if(x < 2) return false;
for(int i = 2; i <= sqrt(x); i++)
{
if(x % i == 0) return false;
}
return true;
}
2、i × i ≤ x
bool is_prime(int x)
{
// 质数大于1
if(x < 2) return false;
for(int i = 2; i * i <= x; i++)
{
if(x % i == 0) return false;
}
return true;
}
3. 推荐此方法i ≤ n / i
bool is_prime(int x)
{
// 质数大于1
if(x < 2) return false;
for(int i = 2; i <= x / i; i++)
{
if(x % i == 0) return false;
}
return true;
}
试除法判定质数
bool is_prime(int x)
{
if (x < 2) return false;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
return false;
return true;
}
试除法分解质因数
void divide(int x)
{
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
{
int s = 0;
while (x % i == 0) x /= i, s ++ ;
cout << i << ' ' << s << endl;
}
if (x > 1) cout << x << ' ' << 1 << endl;
cout << endl;
}
(1)朴素筛法求素数
朴素筛法O(nlogn)
算法核心:把每个数的所有倍数筛掉
调和级数:1 + 1/2 + 1/3 +…+ 1/n = lnn + c(c欧拉常数=0.577)
算法时间复杂度:最外层遍历整个数组是n(其实不用管,只用看内部总次数即可),内部循环总次数是n/2,n/3,n/4…1,累加得n(1/2 + 1/3 + 1/4 +…+1/n)=nlnn=nlogn
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (st[i]) continue;
primes[cnt ++ ] = i;
for (int j = i + i; j <= n; j += i)
st[j] = true;
}
}
//void get_prime(int x)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++] = i;
for(int j = i + i ; j <= n ; j += i) st[j] = true;
}
}
(2)埃式筛法O(nloglogn)
算法核心:把每个质数的所有倍数筛掉
质数定理:1~n中由n/logn个质数
算法时间复杂度:由(1)可得:O(nlonglongn)当数据不是足够大时与O(n)接近
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (st[i]) continue; //st如果是true 说明被筛过,那么它的倍数肯定被筛过,所以直接跳过
//接下来对该质数的所有倍数进行筛选
primes[cnt ++ ] = i;
for (int j = i + i; j <= n; j += i)
st[j] = true;
}
}
(3)线性筛法求素数
算法核心:x只会被它的最小质因数筛去,即每个数字只被筛选一次,因此是线性的n。
证明每个x都能被筛掉:
对于一个合数x,x一定存在一个最小质因子,假设pj是x 的最小质因子,当i枚举到x/pj时,x就被筛了,因为x只有一个最小质因数,因此每个数字只被筛选一次。
算法时间复杂杂度:因为每个数只被筛过一次,因此为O(n)
void get_prime(int x)
{
for(int i = 2 ; i <= x ; i++)
{
if(!st[i]) primes[cnt ++] = i;
/**
for循环判断语句中不需要j<cnt。分两种情况。
1.i为合数,当primes[j]取到i的最小质因子时就break 此时 j<cnt
2.i为质数,当primes[j]的值和i相等时就break 此时j == cnt-1
**/
for(int j = 0 ; primes[j] <= x / i ; j++)
{
st[primes[j] * i] = true; //筛去primes[j]的倍数
/*
针对st[primes[j] * i] = true;本质上分两种情况
1.i%pj == 0, 因为primes[j]是顺序遍历,因此当当一次模为零时,primes[j]一定为i的最小质因
子,primes[j]也一定为primes[j]*i的最小质因子
2.i%pj != 0, 同样因为primes[j]是顺序遍历,primes[j]一定小于i的所有质因子
所以primes[j]也一定为primes[j]*i最小质因子
*/
if(i % primes[j] == 0) break;//当primes[j]是i的最小质因数时break(为了
//遵守算法的核心,避免重复的筛选)。如果继续用primes[j+1]去筛选,此时,
//primes[j+1]大于i的最小质因子,那么也同样不是primes[j+1]*i的最小质因子
}
}
}
模板:
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
二、约数
根据分摊分析,当数据最够多时,每个数的约数平均为logn个。
(第一个数是n个数的约数 , 第二个数是n/2个数的约数 , 以此类推第n个数是n/n个数的约数。
累加得n(1/1+1/2+1/3+…+1/n)=n(lnn+c)≈nlogn)
(1)试除法O(sqrt(n))
思路:从小到大枚举较小的约数即可
vector<int> get_divisors(int x)
{
vector<int> res;
for(int i = 1 ; i <= x / i ; i++)
{
if(x % i == 0)
{
res.push_back(i);
if(i != x / i) res.push_back(x / i); //特判边界
}
}
sort(res.begin() , res.end());
return res;
}
(2)约数个数
题目:给定n个正整数ai,请你输出这些数的乘积的约数个数,答案对109+7取模。
算法思想:
基于算数基本定理:N = p1a1 * p2a2 * … * pkak
N的任意一项约数可以写成 d = q1b1+q2b2+…+qkbk
不同的b数组组合而成的约数d是不同(即因式分解不同)
同理不同的a数组组合而成的N也是不同的,
而a1有a1+1种选法,a2有a2+1种选法…ak有ak+1种选法
因此约数个数:(a1+1)(a1+1)(a3+1)…(ak+1)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int P = 1e9 + 7;
int main()
{
unordered_map<int , int> primes; //利用哈希表存储
int n;
cin >> n;
while(n --) //分解质因数
{
int x;
cin >> x;
for(int i = 2 ; i <= x / i; i++)
{
while(x % i == 0)
{
primes[i]++;
x /= i;
}
}
if(x > 1) primes[x]++;
}
ll ans = 1;
for(auto p : primes) //迭代一次,套用公式即可
ans = ans * (p.second + 1) % P;
cout << ans << endl;
return 0;
}
(3)约数之和
同样的某个数N可以展开为 N = p1a1 * p2a2 * … * pkak
约数之和为:(p10+p11+p12+…+p1a1) * (p20+p21+p22+…+p2a2) * …* (pk0+“pk1+pk2+…+pkak)
即排列问题,展开后就是每一个约数,且都不相等
//求质因数与上方代码相同
for(auto t : primes)
{
int p = t.first , q = t.second;
ll res = 1;
while(q--) res = (res * p + 1) % P; //这里有一个小技巧><
ans = ans * res % P;
}
(4) 最大公约数
(greast common divisor简称“gcd”)
递归版辗转相除法(欧几里得算法):核心是gcd(a , b) = gcd(b , a % b)
原理:
由基本定理得:当d能分别整除a,b时,d就能整除xa+yb。
显然a % b = a – c * b(其中c=a/b)。
即证:(a , b) = (b , a – c * b)
记d=(a,b),则d|a,d|b,所以根据基本定理得d|a-cb,所以d=gcd(b , a-cb)
记d=(b , a-cb) , 则d|b , d|a-cb ,所以根据基本定理得:d|(cb)+(a-cb) 即a|b ,所以d=(a , b)
所以(a , b) = (b , a-c*b)成立,说明(a,b)的公约数就是(b , a – c * b)的公约数,所以等号两边的最大公约数相同。
不断地辗转相除直到第二个参数为0,因为0模上任何一个非零的整数都是0,所以任何一个数都可以看作是0的约数,而b的最大约数是b,那取交集后,gcd(b,0)当然是b。
所以gcd(a , b) = gcd(b , a % b)成立
三、欧拉函数
欧拉函数 O(N)=1到N中所有与N互质的数的个数,如果可以把N写成它的分解质因数公式:
N=p1的a1次方 * p2的a2次方 * …..pk的ak次方
则它的欧拉函数等于N*(1-1/p1)*(1-1/p2)*…(1-1/pk),这是由容斥原理得到的(数学集合论),
我们将n减去所有它的因子的倍数,这其中有些数被减了两次,如p1,p2共同的倍数,我们再逐一加上每两个数的倍数,再减去每三个数的倍数…就能得到与N互质的数的个数了。
1 ~ N 中与 N 互质的数的个数被称为欧拉函数
欧拉函数的证明
利用容斥原理,求1 ~N-1中与N互斥的数的个数s
拆分出N的质因子p1、p2、p3…
s = N – N/p1 – N/p2 – N/p3-…-N/pk
+N/(p1*p2) + N/(p1*p2) + … + N/(p1*pk) + … + N/(pk-1*pk)
– N/(p1*p2*p3) – N/(p1*p2*p4) – … -N/(pk-2*pk-1*pk)
+N/(p1*p2*p3*p4) + … + N/(pp-3*pp-2*pp-1*pp)
…(以此类推)
p1的倍数由N/p1个,p2的倍数有N/p2个…pk的倍数有N/pk个,因此要减去。
但是有的数同时是p1和p2的倍数,所以会被重复减去,因此在第二行加回。
但是有的数同时是p1、p2、p3的倍数,在第一行会被重复减去三次,而在第二行会重复加回三次,相当于没变,因此要在第三行减去。
以此类推。。。。。。。
最后欧拉函数的公式如下:s = N * (1-1/p1) * (1-1/p2) * (1-1/p3) … * (1-1/pk)
接下来用公式来求欧拉函数 O(n*sqrt(n))
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;//数据范围较大记得用long long
const int N = 110;
int n;
int main()
{
cin >> n;
while(n--)
{
int cnt = 0;
ll primes[N];
int x;
cin >> x;
ll ans = x;
for(int i = 2 ; i <= x / i ; i++)
{
if(x % i == 0)
{
ans = ans / i * (i - 1);
while(x % i == 0) x /= i;
}
}
if(x > 1) ans = ans / x * (x - 1);
cout << ans << endl;
}
return 0;
}
筛法求欧拉函数
线性筛法求欧拉函数之和O(n)
核心:在找到质数和筛掉和筛掉合数时,利用欧拉函数的公式直接计得出其欧拉函数
int primes[N], cnt; // primes[]存储所有素数
int euler[N]; // 存储每个数的欧拉函数
bool st[N]; // st[x]存储x是否被筛掉void get_eulers(int n)
{
euler[1] = 1;
for (int i = 2; i <= n; i ++ )
{
if (!st[i])
{
primes[cnt ++ ] = i;
euler[i] = i - 1;
}
for (int j = 0; primes[j] <= n / i; j ++ )
{
int t = primes[j] * i;
st[t] = true;
if (i % primes[j] == 0)
{
euler[t] = euler[i] * primes[j];
break;
}
euler[t] = euler[i] * (primes[j] - 1);
}
}
}
欧拉定理
定理:若a与n互质,则aΦ(n) ≡ 1(mod n)
证明:
假如1 ~ n中,所有与n互质的数是A数组:a1、a2、a3…aΦ(n)
设M数组:aa1、aa2、aa3…aaΦ(n)(同样与n互质)
下面先证明两个推理:
一、M数列中不存在两个数模n同余。
用假设法证明:
1.假如M数列存在ma与mb模n同余,即ma≡mb(mod n)
2.移项得mi – mj ≡ 0 (mod n)
3.即aai-aaj ≡ 0 (mod n)
4.提取公因式得:a(ai-aj) ≡ 0 (mod n)
5.因为a与n互质,所以要是等式左边与n互质,那么必然:(ai-aj) ≡ 0 (mod n)
6.则ai ≡ aj(mod n),这显然与A数组中的数的性质相违背(A数组中各个数都小于n,并且不同,因此不可能模n同余)。
7.所以假设不成立!即:M数列中不存在两个数模n同余!
二、M中的数对n的余数全部与n互质(即mi%n 与 n 互质)
证明:
1.已知a与n互质,ai与n互质,则aai也与n互质,也可得M数列中的数与n互质。
2.然后带入欧几里得算法中推导即可:gcd(aai , n) = gcd(n , aai%n ) = 1 , 即mi%n 与 n 的最大公约数是1
(a与n互质,pi与n互质,因此api与n互质)
3.得证:M中的数对n的模全部与n互质!
根据这两个推理,可以开始推导欧拉定理。
根据推理二,我们可以知道M中的数模n全部与n互质,而且M中不
存在两两对n取模相等的数,而且A、M数组长度相同,因此一个M中的数一定
可以在A中找到唯一一个数和它模n同余(即两个数组在模n的意义下是等价的),因此可得两个数列分别的乘积对n同余
根据A数组的含义,A数组模n后的数组就是A数组本身
即:m1m2m3m4…mΦ(n) ≡ a1a2a3…aΦ(n) (mod n)
将每项m展开的:a * a1 * a * a2 * a * a3…a * aΦ(n) ≡ a1a2a3…aΦ(n) (mod n)
化简得:aΦ(n)(a1a2a3…aΦ(n)) ≡ a1a2a3… aΦ(n) (mod n)
因A数列中的每一项都跟n互质,那么整个数列的乘积也和n互质,所以
可以两边同除a1a2a3…aΦ(n)得:aΦ(n) ≡ 1 (mod n)
证毕!
费马小定理
由欧拉定理可以马上推得费马定理。
当n为质数时,Φ(n) = n – 1
因此当p是质数时,ap-1≡ 1 (mod p) 即费马定理!
四、快速幂
算法核心:将b用二进制表示,然后对每一位进行01判断,进而累乘即可。
求 m^k mod p,时间复杂度 O(logk)。
int qmi(int m, int k, int p)
{
int res = 1 % p, t = m;
while (k)
{
if (k&1) res = res * t % p;
t = t * t % p;
k >>= 1;
}
return res;
}
快速幂求逆元
题目:给定n组ai , pi,其中pi是质数,求ai模pi的乘法逆元,若逆元不存在则输出impossible。
逆元定义:若整数b,p互质,并且对于任意的整数 a,如果满足b|a=0,则存在一个整数x,使得a/b≡a∗x(mod p),则称x为b的模p乘法逆元,记为b−1(mod p)。
接下来进行推导:
若:a/b≡a∗x(mod p)
两边同除a,得:1/b ≡ x (mod p)
移项得:x*b ≡ 1 (mod p) ,即x满足该式子即可!
由费马小定理得:若p是质数,且b不是p的倍数, 则bp-1 ≡ 1 (mod p)
因此x = b p-2 就是解。
当b%p = 0时 ,x*b ≡ 1 (mod p)显然无解
//代码中的a是上面文字中的b
#include <iostream>
using namespace std;
typedef long long ll;
//求a的b次方
ll qmi(ll a , ll b , ll p)
{
ll ans = 1;
while(b)
{
if(b & 1) ans = ans * a % p;
b >>= 1;
a = a * a % p;
}
return ans;
}
int main()
{
int n;
cin >> n;
while(n--)
{
ll a , p;
cin >> a >> p;
ll t = qmi(a , p-2 , p);
if(a % p) cout << t << endl;
else puts("impossible");
}
return 0;
}
欧几里得算法
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
求欧拉函数
int phi(int x)
{
int res = x;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
{
res = res / i * (i - 1);
while (x % i == 0) x /= i;
}
if (x > 1) res = res / x * (x - 1);
return res;
}
五、扩展欧几里得算法
题目:给定n对正整数ai , bi,对于每对数,求出一组xi,yi,使其满足ai∗xi+bi∗yi=gcd(ai,bi)。
裴蜀定理:若a,b是整数,且gcd(a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立。
显然因为d|a , d|b , 则d|ax+by。
有一个直接的应用就是 如果ax+by=1有解,那么gcd(a,b)=1;
根据裴蜀定理,我们知道ai∗xi+bi∗yi=gcd(ai,bi)一定存在解,要是想求出x,y就得用到扩展欧几里得算法。
需要找出递归关系
求解方程 ax+by=gcd(a,b)
当 b=0 时, ax+by=a 故而 x=1,y=0。
当b != 0 时,因为gcd(a,b)=gcd(b,a%b)
而gcd(a,b) = xa+yb , gcd(b,a%b) = yb+x(a%b) . 其中 a%b = a – (a/b)b
所以 gcd(b , a%b) = yb+x(a – (a/b)b) , 化简得:gcd(b , a%b) = xa+(y-(a/b)x)b
推得:xa+yb = xa+(y-(a/b)x)b
根据恒等定理得:y = (y-(a/b) * x) 这就是递归关系。
#include <bits/stdc++.h>
using namespace std;
void exgcd(int a , int b , int &x , int &y)
{
if(!b)//终止条件
{
x = 1 , y = 0;
return;
}
exgcd(b , a % b , y , x);//这里将y写前面,x写后面可以简化代码,否则要进行交换
y -= a / b * x;
/*这是不交换x,y的写法
exgcd(b, a%b, x, y);
int t = y;
y = x - (a/b) * y;
x = t;
*/
return ;
}
int main()
{
int n;
cin >> n;
while(n--)
{
int a , b , x , y;
cin >> a >> b;
exgcd(a , b , x , y);
printf("%d %d\n" , x , y);
}
return 0;
}
模板:
// 求x, y,使得ax + by = gcd(a, b)
int exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1; y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= (a/b) * x;
return d;
}
通解 = 特解 + 齐次解
而齐次解即为方程 ax+by=0的解
通解为 x=x′+k∗b/d , y=y′−k∗a/d ,k∈z
利用扩展欧几里德算法求解线性同余方程
题目:给定n组数据ai,bi,mi,对于每组数求出一个xi,使其满足ai∗xi≡bi(mod mi),如果无解则输出impossible。
算法核心:将原方程进行等价代换:
1.ax≡b (mod m) 等价于 ax+my≡b (mod m)
2.即 (ax+my)%m=b
3.只要利用扩展欧几里德算法求出gcd(a,m),如果b是gcd(a,m)的倍数,那么显然可以通过乘积的方式,来使ax+my等于b,否则返回impossible。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int exgcd(int a, int b , int &x , int &y )
{
if(!b)
{
x = 1 , y = 0;
return a;
}
int d = exgcd(b , a % b , y , x);
y -= a / b * x;
return d;
}
int main()
{
int n;
cin >> n;
while(n--)
{
int a , b , m , x , y;
cin >> a >> b >> m;
int d = exgcd(a , m , x , y);//求gcd(a,m)
if(b % d) puts("impossible");
else cout << (ll) x * b / d % m << endl;//如果b是最大公约数d的倍数,则可以通过乘上一个b/d来使求得的结果由d变成b
}
return 0;
}
六、中国剩余定理
描述:给定 2n 个整数a1,a2,…,an和m1,m2,…,mn,求一个最小的非负整数 x,满足∀i∈[1,n],x≡mi(mod ai)。
思路:
合并:将第一条和第二条合并,再合并进第三条……一直合并n-1次,就只剩一条了。
具体实现:1.由题意得x % a1 = m1 , x % a2 = m2,
2.即x = k1a1 + m1 , x = k2a2+m2,
3.取出两式等号右边得:k1a1 + m1 = k2a2+m2
4.移项得:k1a1-k2a2 = m2-m1.( * )
5.接下来利用扩展欧几里得算法求得k1的解和最大公约数d,判断d是否能整除m2-m1,若不行说明无解,否则继续
6.再将k1自乘上一个(m2-m1)/d才是( * )的一个解,可以知道k1的通解是k1+ka2/d,k2的通解是k2+ka1/d
7.为了防止数据溢出,我们需要求得k1的最小正整数解,在c++中,取模会得到负值,因此我们需要以下操作
8.令t=a2/d,k1 = (k1 % t + t) % t
9.将k1= k1+ka2/d,代回x = k1a1 + m1中得:x = k1a1+m1+ka1a2/d
10.发现此时x的表达式和原来的很像,一部分常量,一部分变量,所以我们重新赋值 , m1 = k1a1+m1,a1= abs(a1 / d * a2)
11.这样一来原来的两条式子就合并为一条x=k1a1+m1(此时a1和m1已经变了),继续合并即可。
12.最后出m1就是解,在10中可以发现m1=k1a1+m1就是x的值,不过在输出也要对其a1取模以输出最小的非负整数解。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll exgcd(ll a , ll b , ll &x , ll &y)
{
if(!b)
{
x = 1 , y = 0;
return a;
}
int d = exgcd(b , a % b , y , x);
y -= a / b * x;
return d;
}
int main()
{
int n;
cin >> n;
ll a1 , m1;
cin >> a1 >> m1;
bool flag = true;
for(int i = 0 ; i < n - 1 ; i++)
{
ll a2 , m2;
cin >> a2 >> m2;
ll k1 , k2;
ll d = exgcd(a1 , a2 , k1 , k2);
if((m2 - m1) % d)
{
flag = false;
break;
}
k1 *= (m2 - m1) / d;//此时求出来的k1只是众多k1的解中的一个而已
ll t = a2 / d;//防止溢出,要求得k1的最小正整数解,易得k1+k*(a2/d)是k1的通解,因此使其对t 取模
k1 = (k1 % t + t) % t;//在c++中,取模的值可得负数,在这样的操作之后会变成同等意义的正数
m1 = a1 * k1 + m1;
a1 = abs(a1 / d * a2);
}
if(flag) cout << (m1 % a1 + a1) % a1 << endl;
else puts("-1");
return 0;
}
七、高斯消元
描述:解一个包含n个方程n个未知数的线性方程组

算法流程:对每一列的系数进行如下操作
1.找到一列中系数绝对值最大的一条方程(不考虑已经移动过的方程)
2.将其移到最上方(同样不考虑移动过的方程)
3.将该系数变为1
4.将下面的方程同一列的系数消为0
5.得到一个倒三角形方程组,即可求出解
得出三种情况:
①完美在倒三角i选哪个 唯一解
②0 = 非0 无解
③0 = 0 无穷解
// a[N][N]是增广矩阵
int gauss()
{
int c, r;
for (c = 0, r = 0; c < n; c ++ )
{
int t = r;
for (int i = r; i < n; i ++ ) // 找到绝对值最大的行
if (fabs(a[i][c]) > fabs(a[t][c]))
t = i;
if (fabs(a[t][c]) < eps) continue;
for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]); // 将绝对值最大的行换到最顶端
for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c]; // 将当前行的首位变成1
for (int i = r + 1; i < n; i ++ ) // 用当前行将下面所有的列消成0
if (fabs(a[i][c]) > eps)
for (int j = n; j >= c; j -- )
a[i][j] -= a[r][j] * a[i][c];
r ++ ;
}
if (r < n)
{
for (int i = r; i < n; i ++ )
if (fabs(a[i][n]) > eps)
return 2; // 无解
return 1; // 有无穷多组解
}
for (int i = n - 1; i >= 0; i -- )
for (int j = i + 1; j < n; j ++ )
a[i][n] -= a[i][j] * a[j][n];
return 0; // 有唯一解
}
八、递归法求组合数
1.题目:给定n组询问,每组询问给定两个整数a,b,请你输出Cba mod (109+7)的值。1≤n≤10000,1≤b≤a≤2000. O(N2)
数据较小,共有2000*2000=4e6中形式,直接暴力,先预处理每一种形式的值,再查询即可。
利用这条关系式:Cba = Cba-1 + Cb-1a-1,打个比方:Cba就是从a个苹果中拿b个,所有的拿法可以分成包括某个特殊的苹果,和不包括某个特殊的苹果,包括的情况则Cb-1a-1,不包括则是Cba-1,加起来就是Cba。
// c[a][b] 表示从a个苹果中选b个的方案数
for (int i = 0; i < N; i ++ )
for (int j = 0; j <= i; j ++ )
if (!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
通过预处理逆元的方式求组合数
首先预处理出所有阶乘取模的余数fact[N],以及所有阶乘取模的逆元infact[N]
如果取模的数是质数,可以用费马小定理求逆元
#include <bits/stdc++.h>
using namespace std;
const int N = 2010;
const int P = 1e9 + 7;
int t[N][N];
int main()
{
for(int i = 0 ; i < N ; i++)
for(int j = 0 ; j <= i ; j++)
{
if(!j) t[j][i] = 1;
else t[j][i] = (t[j][i - 1] + t[j - 1][i - 1]) % P;//递推式
}
int n;
cin >> n;
while(n--)
{
int a, b;
cin >> a >> b;
cout << t[b][a] << endl;
}
return 0;
}
2题目:1≤n≤10000, 1≤b≤a≤105 (NlonN)
1e5 * 1e5 = 1e10,此时情况就太多了,就不能用之前的预处理了。
还知道Cba = a!/(b!*(a-b)!),所以我们可以预处理每一个数的阶乘先,然后在查询即可。
因为a/b mod p != (a mod p)/(b mod p),所以我们要转换成乘法,就要用到逆元。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010;
const int P = 1e9 + 7;
int fact[N] , infact[N];//infact[i]是fact[i]的逆元,因为P是质数,所以可以用费马小定理,快速幂求逆元。
int qmi(int a, int b , int p)//求
{
int res = 1;
while(b)
{
if(b & 1) res = (ll)res * a % p;
b >>= 1;
a = (ll)a * a % p;
}
return res;
}
int main()
{
fact[0] = infact[0] = 1;
for(int i = 1 ; i < N ; i++)
{
fact[i] = (ll)i * fact[i - 1] % P;
infact[i] = (ll)qmi(i , P - 2 , P) * infact[i - 1] % P;
}
int n;
cin >> n;
while(n--)
{
int a , b;
cin >> a >> b;
cout << (ll)fact[a] * infact[b] % P * infact[a - b] % P << endl;
}
return 0;
}
int qmi(int a, int k, int p) // 快速幂模板
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
// 预处理阶乘的余数和阶乘逆元的余数
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
3.题目:给定n组询问,每组询问给定三个整数a,b,p,其中p是质数,请你输出Cba mod p的值。1≤n≤20,1≤b≤a≤1018,1≤p≤105。
这里a和b的数据很大,要用到Lucas(鲁卡斯定理)
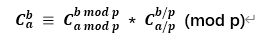
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int p;
int qmi(int a, int b)//快速幂求逆元
{
int res = 1;
while(b)
{
if(b & 1) res = (LL) res * a % p;
b >>= 1;
a = (LL) a * a % p;
}
return res;
}
int C(int a , int b)
{
if(a < b) return 0;
int res = 1;
for(int i = b , j = a ; i ; i-- , j--)//利用定义求出C
{
res = (LL) res * j % p;
res = (LL) res * qmi(i , p - 2) % p;//利用逆元求
}
return res;
}
int lucas(LL a, LL b)
{
if(a < p && b < p) return C(a , b);
return (LL)C(a % p , b % p) * lucas(a / p , b / p) % p;
}
int main()
{
int n;
cin >> n;
while(n--)
{
LL a , b;
cin >> a >> b >> p;
cout << lucas(a , b) << endl;
}
return 0;
}
4.题目:输入a,b,求Cba的值,1≤b≤a≤5000。
注意结果可能很大,需要使用高精度计算。
算法思路:
1.分解质因数,将Cba=a!/(b!*(a-b)!)分解质因数 p1k1 *p2k2 *p3k3 …pnkn ,求出最终每一个质因数的次数
2.高精度乘法
求a!中p的次数O(logp):
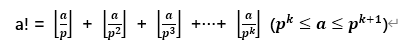
#include <bits/stdc++.h>
using namespace std;
const int N = 5010;
int primes[N];
int cnt;
int sum[N];
bool st[N];
int get(int n , int p)//返回n的阶乘中 ,p的次数
{
int s = 0;
while(n)
{
s += n / p;
n /= p;
}
return s;
}
vector<int> mul(vector<int> a , int b)//高精度乘法
{
vector<int> ans;
int t = 0;
for(int i = 0 ; i < a.size() || t ; i++)
{
if(i < a.size()) t += a[i] * b;
ans.push_back(t % 10);
t /= 10;
}
return ans;
}
void get_primes(int n)//线性筛质数
{
for(int i = 2 ; i <= n ; i++)
{
if(!st[i]) primes[cnt++] = i;
for(int j = 0 ; primes[j] * i <= n ; j++)
{
st[primes[j] * i] = true;
if(i % primes[j] == 0) break;
}
}
}
int main()
{
int a, b;
cin >> a >> b;
get_primes(a);
for(int i = 0 ; i < cnt ; i++)//求出最终每一个p的次数
{
int p = primes[i];
sum[i] = get(a , p) - get(b , p) - get(a - b , p);
}
vector<int> res;
res.push_back(1);
for(int i = 0 ; i < cnt ; i++)//累乘
for(int j = 0 ; j < sum[i] ; j++)
res = mul(res , primes[i]);
for(int i = res.size() - 1 ; i >= 0 ; i--) cout << res[i];
cout << endl;
return 0;
}
Lucas定理
若p是质数,则对于任意整数 1 <= m <= n,有:
C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p)
int qmi(int a, int k, int p) // 快速幂模板
{
int res = 1 % p;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int C(int a, int b, int p) // 通过定理求组合数C(a, b)
{
if (a < b) return 0;
LL x = 1, y = 1; // x是分子,y是分母
for (int i = a, j = 1; j <= b; i --, j ++ )
{
x = (LL)x * i % p;
y = (LL) y * j % p;
}
return x * (LL)qmi(y, p - 2, p) % p;
}
int lucas(LL a, LL b, int p)
{
if (a < p && b < p) return C(a, b, p);
return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
九、容斥原理
集合数为奇数——正好
偶数——负号
判断集合个数
在本题中,判断1-n中包含质数p1的个数为 n / p1,向下取整。
同时有可能存在同时是p1 和p2 的倍数,出现重复相加的情况,要减去,于是 n / (p1*p2)。
以此类推,每次要求的就是包含不同集合的情况下的个数。
程序设计思路
由于可能项较多,我们枚举所有可能项——一般用位运算来做
这样可以对应所有的选法,
从1- 2的n次方-1,将他们转换成二进制表示,0表示不选,1表示选,这样可以包含其中的所有情
判断第k位是不是1, i >> k & 1
题目:
给定一个整数 n 和 m 个不同的质数 p1,p2,…,pm。
请你求出 1∼n 中能被 p1,p2,…,pm 中的至少一个数整除的整数有多少个。
模板:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 20;
int p[N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i ++ ) cin >> p[i];
int res = 0;
for (int i = 1; i < 1 << m; i ++ )
{
int t = 1, s = 0;
for (int j = 0; j < m; j ++ )
if (i >> j & 1)
{
if ((LL)t * p[j] > n)
{
t = -1;
break;
}
t *= p[j];
s ++ ;
}
if (t != -1)
{
if (s % 2) res += n / t;
else res -= n / t;
}
}
cout << res << endl;
return 0;
}
容斥原理一般用来包含这多个集合的求个数
需要
1、集合构造
2、集合个数求解
3、对于重合部分的集合个数求解
这三步是看题目自己分析
分解质因数法求组合数
当我们需要求出组合数的真实值,而非对某个数的余数时,分解质因数的方式比较好用:
1. 筛法求出范围内的所有质数
2. 通过 C(a, b) = a! / b! / (a – b)! 这个公式求出每个质因子的次数。 n! 中p的次数是 n / p + n / p^2 + n / p^3 + …
3. 用高精度乘法将所有质因子相乘
int primes[N], cnt; // 存储所有质数
int sum[N]; // 存储每个质数的次数
bool st[N]; // 存储每个数是否已被筛掉
void get_primes(int n) // 线性筛法求素数
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
int get(int n, int p) // 求n!中的次数
{
int res = 0;
while (n)
{
res += n / p;
n /= p;
}
return res;
}
vector<int> mul(vector<int> a, int b) // 高精度乘低精度模板
{
vector<int> c;
int t = 0;
for (int i = 0; i < a.size(); i ++ )
{
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (t)
{
c.push_back(t % 10);
t /= 10;
}
return c;
}
get_primes(a); // 预处理范围内的所有质数
for (int i = 0; i < cnt; i ++ ) // 求每个质因数的次数
{
int p = primes[i];
sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i ++ ) // 用高精度乘法将所有质因子相乘
for (int j = 0; j < sum[i]; j ++ )
res = mul(res, primes[i]);
卡特兰数( Cn2n / (n+1))
给定n个0和n个1,它们按照某种顺序排成长度为2n的序列,满足任意前缀中0的个数都不少于1的个数的序列的数量为: Cat(n) = C(2n, n) / (n + 1)
举个例子:n=6时,就可以画成上图,假设向右是0向上是1,则在红线以下的路径是合法的,可以看出每一条从(0,0)走到(6,6)的非法路径做关于红线的对称,都对应一条(0,0)-(5,7)的路径;反之,每一条从(0,0)-(5,7)的路径都对应一条从(0,0)-(6,6)的非法路径,那么就可以利用(0,0)-(5,7)的路径数间接求出(0,0)-(6,6)的非法路径数。
算法核心:每一条从(0,0)走到(n,n)的非法路径都对应一条从(0,0)走到(n-1,n+1)的非法路径,因此合法路径就是
因此从(0,0)走到(6,6)的不合法路径数就是Cn-12n,即合法的是Cn2n-Cn-12n ,化简得 Cn2n / (n+1),
所以直接从定义出发求出Cn2n ,其中因为模上一个质数,可以用快速幂求逆元。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 100010 , mod = 1e9 + 7;
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int main()
{
int n;
cin >> n;
int ans = 1;
for(int i = 2 * n ; i > n ; i--) ans = (LL) ans * i % mod;
for(int i = n ; i >= 1 ; i--) ans = (LL) ans * qmi(i , mod - 2 , mod) % mod;
ans = (LL) ans * qmi(n + 1 , mod - 2 , mod) % mod;
cout << ans << endl;
return 0;
}
十、博弈论
先手必胜和先手必败状态
定义P-position和N-position,其中P代表Previous,N代表Next。直观的说,上一次move的人有必胜策略的局面是P-position,也就是“后手可保证必胜”或者“先手必败”,现在轮到move的人有必胜策略的局面是N-position,也就是“先手可保证必胜”。更严谨的定义是:1.无法进行任何移动的局面(也就是terminal position)是P-position;2.可以移动到P-position的局面是N-position;3.所有移动都导致N-position的局面是P-position。
先手必胜状态(N-position)—— 可以走到某一个必败状态(存在我走的某一步,使得对方是必败状态)
先手必败状态(P-position)—— 走不到任何一个必败状态(我怎么走对方都是赢,对方走不到任何一个必败状态)
NIM游戏 —
给定N堆物品,第i堆物品有Ai个。两名玩家轮流行动,每次可以任选一堆,取走任意多个物品,可把一堆取光,但不能不取。取走最后一件物品者获胜。两人都采取最优策略,问先手是否必胜。
我们把这种游戏称为NIM博弈。把游戏过程中面临的状态称为局面。整局游戏第一个行动的称为先手,第二个行动的称为后手。若在某一局面下无论采取何种行动,都会输掉游戏,则称该局面必败。
所谓采取最优策略是指,若在某一局面下存在某种行动,使得行动后对面面临必败局面,则优先采取该行动。同时,这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况,即两人均无失误,都采取最优策略行动时游戏的结果。
NIM博弈不存在平局,只有先手必胜和先手必败两种情况。
定理: NIM博弈先手必胜,当且仅当 A1 ^ A2 ^ … ^ An != 0
题目
现在,有一个 n 级台阶的楼梯,每级台阶上都有若干个石子,其中第 i 级台阶上有 ai 个石子(i≥1)。
两位玩家轮流操作,每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中(不能不拿)。
已经拿到地面上的石子不能再拿,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
模板
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int main()
{
int n;
scanf("%d", &n);
int res = 0;
for (int i = 1; i <= n; i ++ )
{
int x;
scanf("%d", &x);
if (i & 1) res ^= x;
}
if (res) puts("Yes");
else puts("No");
return 0;
}
公平组合游戏ICG
若一个游戏满足:
由两名玩家交替行动;
在游戏进程的任意时刻,可以执行的合法行动与轮到哪名玩家无关;
不能行动的玩家判负;
则称该游戏为一个公平组合游戏。
NIM博弈属于公平组合游戏,但城建的棋类游戏,比如围棋,就不是公平组合游戏。因为围棋交战双方分别只能落黑子和白子,胜负判定也比较复杂,不满足条件2和条件3。
有向图游戏
给定一个有向无环图,图中有一个唯一的起点,在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动,每次可以移动一步,无法移动者判负。该游戏被称为有向图游戏。
任何一个公平组合游戏都可以转化为有向图游戏。具体方法是,把每个局面看成图中的一个节点,并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。
Mex运算
设S表示一个非负整数集合。定义mex(S)为求出不属于集合S的最小非负整数的运算,即:
mex(S) = min{x}, x属于自然数,且x不属于S
SG函数
在有向图游戏中,对于每个节点x,设从x出发共有k条有向边,分别到达节点y1, y2, …, yk,定义SG(x)为x的后继节点y1, y2, …, yk 的SG函数值构成的集合再执行mex(S)运算的结果,即:
SG(x) = mex({SG(y1), SG(y2), …, SG(yk)})
特别地,整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值,即SG(G) = SG(s)。
有向图游戏的和 —— 模板题 AcWing 893. 集合-Nim游戏
设G1, G2, …, Gm 是m个有向图游戏。定义有向图游戏G,它的行动规则是任选某个有向图游戏Gi,并在Gi上行动一步。G被称为有向图游戏G1, G2, …, Gm的和。
有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数值的异或和,即:
SG(G) = SG(G1) ^ SG(G2) ^ … ^ SG(Gm)
定理
有向图游戏的某个局面必胜,当且仅当该局面对应节点的SG函数值大于0。
有向图游戏的某个局面必败,当且仅当该局面对应节点的SG函数值等于0。
使用Nim模型去求解问题的关键
在于简单判断当前是否为先手必胜状态还是先手必败状态
如果是先手必胜状态则,找到必胜策略。