线性代数笔记(1):线性方程组
2019-10-14
这部分的笔记依据David C. Lay 的
《线性代数及其应用》
第一章内容。
♡ 1 \heartsuit 1
♡
1
线性方程组
1.1 线性方程组
对于包含未知数
x 1 , x 2 , ⋯ , x n x_1, x_2, \cdots, x_n
x
1
,
x
2
,
⋯
,
x
n
的方程:
a 1 x 1 + a 2 x 2 + ⋯ + a n x n = b a_1 x_1 + a_2 x_2 + \cdots + a_n x_n = b
a
1
x
1
+
a
2
x
2
+
⋯
+
a
n
x
n
=
b
,如果其中
b b
b
与系数
a 1 , a 2 , ⋯ , a n a_1, a_2, \cdots, a_n
a
1
,
a
2
,
⋯
,
a
n
是实数或复数,则这个方程就是
线性方程组
;
n n
n
可以是任意正整数。
线性方程组是由一个或几个包含相同变量
x 1 , x 2 , ⋯ , x i x_1, x_2,\cdots, x_i
x
1
,
x
2
,
⋯
,
x
i
的线性方程组成的。而线性方程组的一组
解
是一组数(
s 1 , s 2 , ⋯ , s n s_1,s_2,\cdots,s_n
s
1
,
s
2
,
⋯
,
s
n
),用这组数分别代替
x 1 , x 2 , ⋯ , x i x_1, x_2,\cdots, x_i
x
1
,
x
2
,
⋯
,
x
i
时,
所有
方程的两边相等。
方程组所有可能的解的集合称为线性方程组的解集。当且仅当两个方程组有相同的解集,则两个线性方程组是等价的。
1.2 线性方程组解的情况
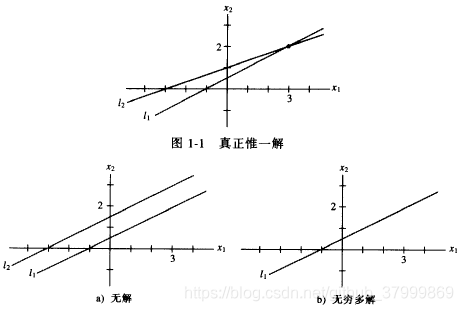
线性方程组的解有下列三种情况:
- 无解
- 有唯一解
- 有无穷多解
当一个线性方程组有一个或
无穷多
个解时,称这个线性方程组是相容的;如无解,则称不相容。
1.3 矩阵
一个线性方程组包含的主要信息可以用一个称为
矩阵
的紧凑的矩形阵列表示,如方程组:
x 1 − 2 x 2 + x 3 = 0 x_1 – 2 x_2 + x_3 = 0
x
1
−
2
x
2
+
x
3
=
0
2 x 2 − 8 X 3 = 8 2 x_2 – 8X_3 = 8
2
x
2
−
8
X
3
=
8
− 4 x 1 + 5 x 2 + 9 x 3 = − 9 -4x_1 + 5x_2 + 9x_3 = -9
−
4
x
1
+
5
x
2
+
9
x
3
=
−
9
把每一个变量的系数写在对其的一列中,矩阵
[ 1 − 2 1 0 2 − 8 − 4 5 9 ] \left[ \begin{matrix} 1 & -2 & 1 \\ 0 & 2 & -8 \\ -4 & 5 & 9 \end{matrix} \right]
⎣
⎡
1
0
−
4
−
2
2
5
1
−
8
9
⎦
⎤
称为上面方程组的
系数矩阵
。而
[ 1 − 2 1 0 0 2 − 8 8 − 4 5 9 − 9 ] \left[ \begin{matrix} 1 & -2 & 1 & 0 \\ 0 & 2 & -8 & 8\\ -4 & 5 & 9 & -9 \end{matrix} \right]
⎣
⎡
1
0
−
4
−
2
2
5
1
−
8
9
0
8
−
9
⎦
⎤
称为方程组的
增广矩阵
。
1.4 线性方程组的解法
线性方程组求解的基本思路是
把方程组用一个更容易解的等价方程组(即有相同解集)代替
。
一个矩阵经过初等行变换后得到的矩阵,与原来的矩阵是
行等价
的,因此两个线性方程组的增广矩阵如果是行等价的则它们有相同的解集。
初等行变换有3中形式:
- (倍加)把某一行的倍数加到玲一行上
- (对换)把两行对换
- (倍乘)把某一行的所有元素乘以同一个非零整数
通过对增广矩阵的初等行变换可以研究关于线性方程组解存在情况的问题:
- 方程组是否相容,即存在至少一组解
- 如果方程组有解,那么解是否唯一
通过初等行变换形成的
阶梯形矩阵
可以判断线性方程组解集存在的情况。
阶梯形矩阵
是指:
- 每一个非零行在每一零行之上
- 某一行先导元素所在的列位于前一行先导元素的右面
- 某一先导元素所在列的下方元素都是零
如果一个阶梯型矩阵还有以下性质,则被称为
简化(行)阶梯形
,:
- 每一非零行的先导元素是1
- 魅影先导元素1是该元素所在列的唯一非零元素
定理1
:
每个矩阵行等价于唯一的简化阶梯型矩阵
阶梯型的矩阵可以参考下图:

非零行的
先导元素
是指该行中最左边的非零元素。
若矩阵
A A
A
等价于阶梯形矩阵
U U
U
,称
U U
U
为
A A
A
的(行)阶梯形。矩阵中的
主元位置
是
A A
A
中对应于它的阶梯形中先导元素的位置,
主元列
是
A A
A
含有主元位置的列。
定理2
:线性方程组相容的充要条件是增广矩阵的最右列不是主元列,就是说,增广矩阵的阶梯形没有形如
[ 0 0 ⋯ b ] \left[ \begin{matrix} 0 & 0 & \cdots & b \end{matrix} \right]
[
0
0
⋯
b
]
的行;若线性方程组相容,它的解集可能有两种情形:(1)当没有自由变量时,有唯一解;(2)若至少有一个自由变量,有无穷多解
若线性方程组的方程个数少于未知数个数,被称为
欠定方程组
,如果一个欠定方程组是相容的,则会有无穷多解;若线性方程组的方程个数多于未知数个数,被称为
超定方程组
,超定方程组可以相容(唯一解或无穷多解)也可能不相容。
应用行简化方法解线性方程组的步骤:
a. 写出线性方程组的增广矩阵
b. 应用行简化方法把增广矩阵化为阶梯形,确定方程组是否有解,如果没有解就停止,否则进行下一步
c. 继续行简化方法得到简化阶梯形
d. 写出由c步所得矩阵所对应的方程组
e. 把d步所得的每个方程改写成为用自由变量表示基本变量的形式
1.5 向量方程
仅含一
列
的矩阵称为列向量,简称
向量
;向量集合用
R n R^n
R
n
表示,
R R
R
表示向量中的元素是实数,指数
n n
n
表示每个向量包含元素的个数。
R n R^n
R
n
中两个向量相等,当且仅当对应元素都相等。
向量在空间中可以视为从原点出发的一个有方向和长度的量,有时会将原点这个前提省略,用向量的终点坐标直接表示向量。
两个同属于向量空间
R n R^n
R
n
的向量相加,就是把对应元素相加得到新的向量。在二维平面中可以图示为平行四边形法则。

R n R^n
R
n
中向量有以下袋鼠性质:对
R n R^n
R
n
中一切向量
u , v , w u, v, w
u
,
v
,
w
以及标量
c c
c
和
d d
d
:
-
(1)
u u
u
+
v v
v
=
v v
v
+
u u
u
-
(2)
u u
u
+
v v
v
+
w w
w
=
u u
u
+ (
v v
v
+
w w
w
) -
(3)
u u
u
+
0 0
0
=
0 0
0
+
u u
u
=
u u
u
-
(4)
u u
u
+ (
− u -u
−
u
) =
− u -u
−
u
+
u u
u
=
0 0
0
-
(5)
c c
c
(
u u
u
+
v v
v
) =
c c
c
u u
u
+
c c
c
v v
v
-
(6)(
c c
c
+
d d
d
)
u u
u
=
c c
c
u u
u
+
d d
d
u u
u
-
(7)
1 1
1
u u
u
=
u u
u
定义线性组合:给定
R n R^n
R
n
中向量
v 1 , v 2 , ⋯ , v p v_1, v_2, \cdots, v_p
v
1
,
v
2
,
⋯
,
v
p
和标量
c 1 , c 2 , ⋯ , c p c_1, c_2, \cdots, c_p
c
1
,
c
2
,
⋯
,
c
p
,向量
y = c 1