[拼音]:paowuxing pianweifen fangcheng
[外文]:partial differential equation of parabolic type
简称抛物型方程,一类重要的偏微分方程。热传导方程是最简单的一种抛物型方程。
热传导方程
研究热传导过程的一个简单数学模型。根据热量守恒定律和傅里叶热传导实验定律导致热传导方程
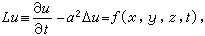
(1)
式中u是温度;Δ是拉普拉斯算符;α2是导温系数;
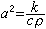
;k是热传导系数;с、ρ分别是比热和密度;
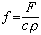
;F是外加热源密度。自然界还有很多现象同样可以用方程(1)来描述,例如分子在介质中的扩散过程等,因此方程(1)通常亦称为扩散方程。
定解问题
为了确定一个具体的热传导过程,除了列出方程(1)以外,还必须知道物体Ω的初始温度(初始条件)和在它的边界嬠Ω上所受到的外界的影响(边界条件)。
初始条件:
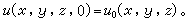
(2)
边界条件,最通常的形式有三类。
第一边界条件(或称狄利克雷条件):
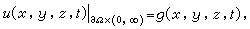
(3)
即表面温度为已知函数。
第二边界条件(或称诺伊曼条件):
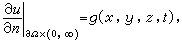
(4)
式中n是嬠Ω的外法向,即通过表面的热量已知。
第三边界条件(或称罗宾条件):

(5)式中α≥0;即物体表面给定热交换条件。
除了以上三类边界条件外还可以在边界嬠Ω上给定其他形式的边界条件,如斜微商条件、混合边界条件等。
方程(1)连同初始