1.相关概念:
相关分析是研究两个或两个以上的变量之间的相关程度及大小的一种统计方法。
回归分析是寻找存在相关关系的变量间的数学表达式,并进行推断的一种统计方法。 在对回归分析进行分类时,主要有两种分类方式:
根据变量的数目,可以分类为一元回归,多元回归; 根据自变量和因变量的表现形式,分为线性和非线性;
所以,回归分析包括四个方向,一元线性回归分析,多元线性回归分析,一元非线性回归分析,多元非线性回归分析。
2.实现功能:
回归分析的流程大致有:
第一步:确认是否是预测问题
第二步:确认要预测的因变量,影响预测结果的自变量
第三步:确定回归模型,建立回归方程
第四步:计算模型,检验结果
第五步:进行预测
本文目的是提供解决的是第三步以及第四步的计算指标的工具类,提供的回归模型为
一元线性回归,多项式回归,多元线性回归
,计算的指标有
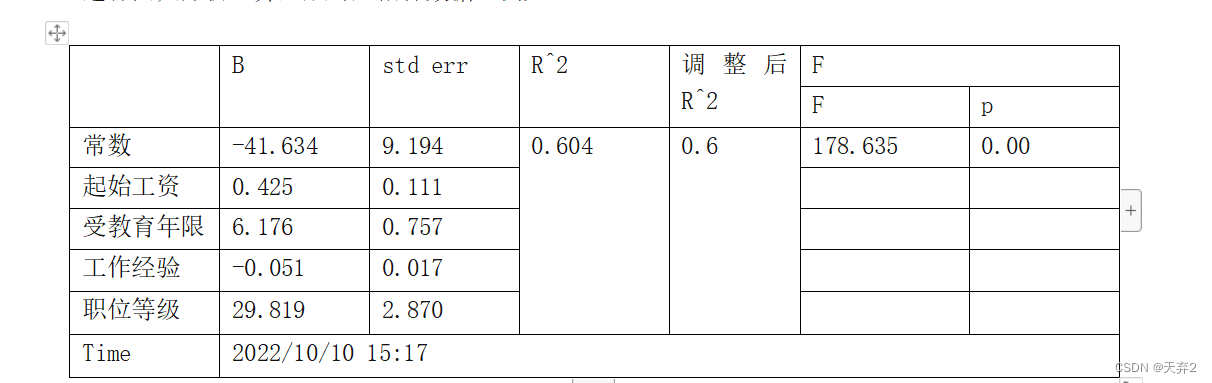
回归系数,系数估计的基本标准误差,R方值,调整R方
,
F检验值
以及对应
P值
例如:
3.导入依赖:
<dependency>
<groupId>net.sf.jsci</groupId>
<artifactId>jsci</artifactId>
<version>1.2</version>
</dependency>
<dependency>
<groupId>org.apache.commons</groupId>
<artifactId>commons-math3</artifactId>
<version>3.6.1</version>
</dependency>
4.Java代码:
Regression类
import org.apache.commons.math3.exception.util.LocalizedFormats;
import org.apache.commons.math3.stat.regression.ModelSpecificationException;
import org.apache.commons.math3.stat.regression.RegressionResults;
import org.apache.commons.math3.stat.regression.SimpleRegression;
public class Regression {
private double rSquared;
private double adjRSquared;
private double[] parameters;
private double[] stdErrors;
private double fValue;
private boolean hasData;
private Integer dfDependent;
private Integer dfIndependent;
public Integer getDfDependent() {
return dfDependent;
}
public void setDfDependent(Integer dfDependent) {
this.dfDependent = dfDependent;
}
public Integer getDfIndependent() {
return dfIndependent;
}
public void setDfIndependent(Integer dfIndependent) {
this.dfIndependent = dfIndependent;
}
public Regression() {
}
public double getRSquared() {
return rSquared;
}
public void setRSquared(double rSquared) {
this.rSquared = rSquared;
}
public double getAdjRSquared() {
return adjRSquared;
}
public void setAdjRSquared(double adjRSquared) {
this.adjRSquared = adjRSquared;
}
public double[] getParameters() {
return parameters;
}
public void setParameters(double[] parameters) {
this.parameters = parameters;
}
public double[] getStdErrors() {
return stdErrors;
}
public void setStdErrors(double[] stdErrors) {
this.stdErrors = stdErrors;
}
public boolean isHasData() {
return hasData;
}
public void setHasData(boolean hasData) {
this.hasData = hasData;
}
public double getFValue() {
return fValue;
}
public void setFValue(double fValue) {
this.fValue = fValue;
}
}
一元线性回归 y = b0 + b1 * x
import org.apache.commons.math3.stat.regression.RegressionResults;
import org.apache.commons.math3.stat.regression.SimpleRegression;
public class SimpleLinearRegression extends Regression{
private final SimpleRegression regression;
public SimpleLinearRegression() {
this.regression = new SimpleRegression();
}
public void addData(final double[][] data) {
regression.addData(data); // 数据集
this.setHasData(true);
RegressionResults results = regression.regress();
this.setParameters(results.getParameterEstimates());
this.setRSquared(results.getRSquared());
this.setAdjRSquared(results.getAdjustedRSquared());
this.setStdErrors(results.getStdErrorOfEstimates());
this.setFValue((results.getRegressionSumSquares()) / (results.getErrorSumSquares() / (data.length -2)) );
}
public String getFunction() {
if (!this.isHasData()) {
return "未构造数据";
}
double b0 = this.getParameters()[0];
double b1 = this.getParameters()[1];
return "f(x) =" +
(b0 >= 0 ? " " : " - ") +
Math.abs(b0) +
(b1 > 0 ? " + " : " - ") +
Math.abs(b1) +
"x";
}
}
多项式回归 y = b0 + b1 * x + b2 * x^2 + …
import org.apache.commons.math3.stat.regression.OLSMultipleLinearRegression;
import java.util.ArrayList;
import java.util.List;
public class PolynomialRegression extends Regression{
private final OLSMultipleLinearRegression ols;
PolynomialRegression() {
ols = new OLSMultipleLinearRegression();
}
public void addData(double[] xArray, double[] yArray, int power) {
double[][] independentVariable = generateVariable(xArray, power);
int dfDependent = yArray.length - power - 1;
ols.newSampleData(yArray, independentVariable);
this.setParameters(ols.estimateRegressionParameters());
this.setStdErrors(ols.estimateRegressionParametersStandardErrors());
this.setRSquared(ols.calculateRSquared());
this.setAdjRSquared(ols.calculateAdjustedRSquared());
this.setDfDependent(dfDependent);
this.setDfIndependent(power);
this.setFValue(((ols.calculateTotalSumOfSquares() - ols.calculateResidualSumOfSquares()) / power) / (ols.calculateResidualSumOfSquares() / dfDependent));
this.setHasData(true);
}
/**
* 生成多项式自变量数据
*/
public static double[][] generateVariable(double[] xArray, int power) {
List<double[]> data = new ArrayList<>();
for (final double x : xArray) {
double[] item = new double[power];
for (int i = 0; i < power; i++) {
item[i] = Math.pow(x, i + 1);
}
data.add(item);
}
return data.toArray(new double[0][]);
}
public String getFunction() {
if (!this.isHasData()) {
return "未构造数据";
}
final double[] parameters = this.getParameters();
StringBuilder function = new StringBuilder("y = ");
for (int i = 0; i < parameters.length; i++) {
function.append(parameters[i]);
for (int j = 0; j < i; j++) {
function.append(" x ");
if (j != (i - 1)) {
function.append("*");
}
}
if (i != (parameters.length -1)) {
function.append(" + ");
}
}
return function.toString();
}
}
多元线性回归 f(x, y . . .) = b0 + b1 * x + b2 * y + …
import org.apache.commons.math3.stat.regression.OLSMultipleLinearRegression;
public class MultipleLinearRegression extends Regression{
private final OLSMultipleLinearRegression ols;
MultipleLinearRegression() {
ols = new OLSMultipleLinearRegression();
}
public void addData(double[][] xArray, double[] yArray, int numberOfIndependent) {
int dfDependent = yArray.length - numberOfIndependent - 1;
ols.newSampleData(yArray, xArray);
this.setParameters(ols.estimateRegressionParameters());
this.setStdErrors(ols.estimateRegressionParametersStandardErrors());
this.setRSquared(ols.calculateRSquared());
this.setAdjRSquared(ols.calculateAdjustedRSquared());
this.setDfDependent(dfDependent);
this.setDfIndependent(numberOfIndependent);
this.setFValue(((ols.calculateTotalSumOfSquares() - ols.calculateResidualSumOfSquares()) / numberOfIndependent) / (ols.calculateResidualSumOfSquares() / dfDependent));
this.setHasData(true);
}
public String getFunction() {
if (!this.isHasData()) {
return "未构造数据";
}
final double[] parameters = this.getParameters();
StringBuilder function = new StringBuilder("y = ");
for (int i = 0; i < parameters.length; i++) {
function.append(parameters[i]).append("x").append(i);
if (i != (parameters.length -1)) {
function.append(" + ");
}
}
return function.toString();
}
}
统计工具类(求p值)
import JSci.maths.statistics.FDistribution;
import JSci.maths.statistics.TDistribution;
import org.apache.commons.math3.exception.DimensionMismatchException;
import org.apache.commons.math3.stat.correlation.PearsonsCorrelation;
import org.apache.commons.math3.stat.correlation.SpearmansCorrelation;
import org.apache.commons.math3.stat.descriptive.moment.Mean;
import org.apache.commons.math3.stat.descriptive.moment.StandardDeviation;
import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
/**
* Statistics
* 统计工具类,使用统计工具用于做统计学数据分析,将计算方法进行集成调用
* @author pyy
* @since 2022/9/23 17:07
*/
public class StatisticsUtil {
private final StatisticsUtil stat = new StatisticsUtil();
private static final double NO_VALUE = Double.NaN;
private StatisticsUtil() {
}
public StatisticsUtil getInstance() {
return stat;
}
/**
* 计算数据均值
* @param values 双精度数组
* @return 平均值
*/
public static double computeMean(final double[] values) {
if (testNull(values)) {
return NO_VALUE;
}
Mean mean = new Mean();
return mean.evaluate(values);
}
/**
* 计算数据标准差
* @param values 双精度数组
* @return 标准差
*/
public static double computeStandardDeviation(final double[] values) {
if (testNull(values)) {
return NO_VALUE;
}
StandardDeviation sd = new StandardDeviation();
return sd.evaluate(values);
}
/**
* 获取数据最大值
* @param values 双精度数组
* @return 最大值
*/
public static double getMaxValue(final double[] values) {
if (testNull(values)) {
return NO_VALUE;
}
Arrays.sort(values);
return values[values.length - 1];
}
/**
* 获取数据最小值
* @param values 双精度数组
* @return 最小值
*/
public static double getMinValue(final double[] values) {
if (testNull(values)) {
return NO_VALUE;
}
Arrays.sort(values);
return values[0];
}
/**
* 获取数据最大值和最小值
* @param values - 双精度数组
* @return map<String, Double>
*/
public static Map<String, Double> getMaxAndMin(final double[] values) {
Map<String, Double> result = new HashMap<>(16);
result.put("max", NO_VALUE);
result.put("min", NO_VALUE);
if (testNull(values)) {
return result;
}
Arrays.sort(values);
result.clear();
result.put("max", values[values.length - 1]);
result.put("min", values[0]);
return result;
}
/**
* 计算两个数据之间的相关系数
* @param xArray -- 双精度数组
* @param yArray -- 双精度数组
* @param methodId -- 相关系数方法
* @return double
*/
public static double correlation(final double[] xArray, final double[] yArray, String methodId) {
double value = NO_VALUE;
if (xArray.length != yArray.length) {
throw new DimensionMismatchException(xArray.length, yArray.length);
} else if (xArray.length < 2) {
return value;
} else {
if (PEARSON_ID.equals(methodId)) {
PearsonsCorrelation pearsonsCorrelation = new PearsonsCorrelation();
value = pearsonsCorrelation.correlation(xArray, yArray);
} else if (SPEARMAN_ID.equals(methodId)) {
SpearmansCorrelation spearmansCorrelation = new SpearmansCorrelation();
value = spearmansCorrelation.correlation(xArray, yArray);
}
}
return value;
}
/**
* 计算两个数据之间的相关系数
* @param xArray -- 双精度数组
* @param yArray -- 双精度数组
* @return double
*/
public static double correlation(final double[] xArray, final double[] yArray) {
return correlation(xArray, yArray, PEARSON_ID);
}
/**
* 计算显著性p值算法
* @param rValue 相关系数
* @param n 分析数据的个数
* @param methodId 使用的方法
* @return p-value
*/
public static double getPValue(final double rValue, final int n, String methodId) {
if (n < 2) {
return NO_VALUE;
}
double pValue = NO_VALUE;
double tValue = ((rValue * Math.sqrt(n-2)) / (Math.sqrt(1 - (rValue * rValue))));
int free= n-2;
TDistribution td=new TDistribution(free);
if (PEARSON_ID.equals(methodId)) {
double cumulative = td.cumulative(tValue);
if(tValue>0) {
pValue=(1-cumulative)*2;
}else {
pValue=cumulative*2;
}
} else if (SPEARMAN_ID.equals(methodId)) {
if (n > 500) {
tValue = (rValue * Math.sqrt(n-1));
}
double cumulative = td.cumulative(tValue);
if(tValue>0) {
pValue=(1-cumulative)*2;
}else {
pValue=cumulative*2;
}
}
return pValue;
}
/**
* T检验 - 计算显著性p值算法
* @param rValue 相关系数
* @param n 分析数据的个数
* @return p-value
*/
public static double getPValue(final double rValue, final int n) {
return getPValue(rValue, n, PEARSON_ID);
}
/**
* 判空
* @param values 双精度数组
* @return boolean
*/
private static boolean testNull(final double[] values) {
return values == null;
}
/**
* F检验 - 计算显著性p值算法
* @param fValue f检验值 (ESS/K)/(RSS/(n-k-1))
* @param dgrP X的自由度 即为自变量的个数
* @param dgrQ Y的自由度 样本数 - 自变量个数 -1
* @return P-Value
*/
public static double getPValue(double fValue, int dgrP, int dgrQ) {
FDistribution fd=new FDistribution(dgrP, dgrQ);
double cumulative = fd.cumulative(fValue);
return (1-cumulative);
}
}
常量类(没有会报错)
public class AnalysisConstants {
/**
* pearson常量
*/
public static final String PEARSON_ID = "1001";
public static final String PEARSON_NAME = "pearson";
/**
* spearman常量
*/
public static final String SPEARMAN_ID = "1002";
public static final String SPEARMAN_NAME = "spearman";
public static final String NULL_TARGET = "空指标ID";
}
5.代码测试
一元线性回归测试
public static void test1() {
double[][] data = linearScatters();
SimpleLinearRegression re = new SimpleLinearRegression();
re.addData(data);
System.out.println("R方为"+ re.getRSquared());
System.out.println("调整R方为"+ re.getAdjRSquared());
System.out.println(re.getFunction());
System.out.println("标准误为:" + re.getStdErrors()[0]);
System.out.println("f值:" + re.getFValue() );
System.out.println("f检验P值:" + StatisticsUtil.getPValue(re.getFValue(), 1, data.length - 2));
}
public static double[][] linearScatters() {
List<double[]> data = new ArrayList<>();
for (double x = 0; x <= 10; x += 0.1) {
double y = 1.5 * x + 0.5;
y += Math.random() * 60 - 2; // 随机数
double[] xy = {x, y};
data.add(xy);
}
return data.stream().toArray(double[][]::new);
}
多项式回归测试
public static void test2() {
// 自变量数据
double[] xArray = new double[100];
double k = 0.0;
for (int i = 0; i < 100; i++) {
xArray[i] = k;
k += 0.1;
}
// 因变量数据
double[] yArray = new double[100];
for (int i = 0; i < xArray.length; i++) {
double x = xArray[i];
double x1 = x;
double x2 = x * x;
double x3 = x * x * x;
yArray[i] = 20 + 2 * x1 + 12 * x2 + 8 * x3 + Math.random() * x1 * 500;
}
final PolynomialRegression po = new PolynomialRegression();
po.addData(xArray, yArray, 3);
System.out.println("R方为"+ po.getRSquared());
System.out.println("调整R方为"+ po.getAdjRSquared());
System.out.println(po.getFunction());
System.out.println("标准误为:" + po.getStdErrors()[0]);
System.out.println("f值:" + po.getFValue() );
System.out.println("f检验P值:" + StatisticsUtil.getPValue(po.getFValue(), 3, yArray.length - 4));
}
多元回归分析测试
public static void test3() {
double[][] x = randomX3();
double[] y = randomY3(x);
MultipleLinearRegression mul = new MultipleLinearRegression();
mul.addData(x, y, 2);
System.out.println(mul.getFunction());
System.out.println("标准误: " + mul.getStdErrors()[0]);
System.out.println("R方 : " + mul.getRSquared());
System.out.println("调整后R方 :" + mul.getAdjRSquared());
System.out.println("f值:" + mul.getFValue()) ;
System.out.println("f检验P值:" + StatisticsUtil.getPValue(mul.getFValue(), mul.getDfIndependent(), mul.getDfDependent() ));
}
public static double[][] randomX3() {
List<double[]> data = new ArrayList<>();
for (double i = 0; i < 10; i += 0.1) {
double x1 = i;
double x2 = Math.sqrt(i);
data.add(new double[]{x1, x2});
}
return data.stream().toArray(double[][]::new);
}
public static double[] randomY3(double[][] arr) {
if (arr != null && arr.length > 0) {
int len = arr.length;
double[] y = new double[len];
for (int i = 0; i < len; i++) {
double[] x = arr[i];
// 构造数据
y[i] = functionConstructorY3(x);
}
return y;
}
return null;
}
public static double functionConstructorY3(double[] x) {
double x1 = x[0];
double x2 = x[1];
return 20 + 2 * x1 + 3 * x2 + Math.random() * 30;
}
测试结果

全部的代码都在上面了,如果有缺失的代码可以在评论区提醒一声,顺便提一声,这里的多项式和多元回归实现原理是一样的,这就意味着多元多项的回归模型也能够实现,可以自定义函数实现分析,具体实现我没有去尝试,感兴趣的同学可以理解一下代码流程,尝试一下。
6.业务流程
当要在系统中实现这样的分析功能,可以考虑下面的实现功能
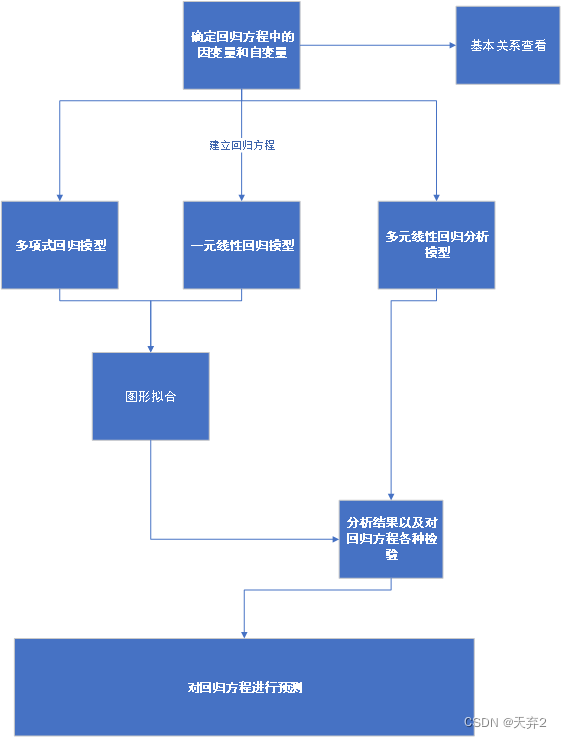
在执行回归分析前,正常会先进行相关分析,可以参考这个连接:
java做相关分析
最后附上我回归分析结果展示(参考python的statsmodels输出)

7.参考