接触雅可比行列式是在二重积分的变量变换中，参见我的另一篇文章

https://blog.csdn.net/xiaoyink/article/details/88432372

下面我们来详细说明一下雅可比行列式和雅可比矩阵

雅可比矩阵

参考维基百科

https://zh.wikipedia.org/wiki/%E9%9B%85%E5%8F%AF%E6%AF%94%E7%9F%A9%E9%98%B5

总结一下，雅可比矩阵可以理解为：

若在n维欧式空间中的一个向量映射成m维欧式空间中的另一个向量的对应法则为

F，F

由m个实函数组成，即：

那么雅可比矩阵是一个m×n矩阵：

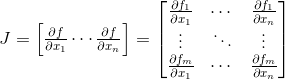
其中输入向量

x

= (x1, … , xn)，输出向量

y

= (y1, …, ym)，

如果p是中的一个点，

F

在p点可微分，根据数学分析，雅可比矩阵

是在这点的导数

在此情况下，

这个线性映射即

F

在点p附近的最优线性逼近，也就是说当 x足够靠近点 p时，我们有

当m = n时，矩阵

就会变成一个方阵，

F

就变成从n维欧式空间到n维欧式空间的映射，方阵的行列式就是雅可比行列式

上式移项得：

即：

和

是向量，n维空间的向量，那么微分的话，就是相等的了：

其中：

,

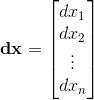
即：

注意dy1dy2dy3···dyn代表的是微元的体积所以其实它们之间是叉乘

由于是叉乘，所以包含所有dxi X dxi 的项结果全是零，所以每一个小括号里面我们都取包含不同dx的项即可，例如

1.第一个小括号里我们取dx1，第二个小括号里取dx2…… 第n个小括号里取dxn，最终形成了

2.第一个小括号里我们取dx2，第二个小括号里取dx1，第三个取dx3，第四个取dx4，第n个取dxn，最终形成了

为了方便提取公因数，我们把上式dx2和dx1交换一下顺序，叉乘交换顺序，变更符号，即：

如此下去，把所有的选项都写出来，并将dx1 X dx2 X··· X dxn 整体提出来，得到的结果如下：

其中j1,j2,···, jn为1,2,···, n的一个排序，

为所有n级排序求和，

表示j1,j2,···,jn的逆序数，我们发现中括号里的部分即为行列式

的定义，所以我们可以将上式化简如下，

即，此微元的体积为:

雅可比行列式

如上形式成为雅可比行列式，网络上有篇文章总结的很好：

http://www.360doc.com/content/18/1003/23/59256698_791725747.shtml

简单来说，在n维欧几里得空间中，行列式描述的是一个线性变换对“体积”所造成的影响，代表着变换后的缩放比例，而雅可比行列式也不例外。

在上述

到

对应法则为

F

的映射过程中，大多数情况

F

都是非线性映射，但是其微元变换实际可以看做是线性的，因此雅可比行列式的实际意义就是坐标变换后单位微元的比率或倍数，即体积比率：

和

分别等于 y系列坐标系和x系列坐标系的单位微元的体积